分类目录：《自然语言处理从入门到应用》总目录

---

若要利用计算机对自然语言进行处理，首先需要解决语言在计算机内部的存储和计算问题。字符串（String）是文本最自然，也是最常用的机内存储形式。所谓字符串，即字符序列，而其中的一个字符本质上就是一个整数。基于字符串的文本表示方式可以实现简单的字符串增删改查等编辑任务，并能够通过编辑距离等算法计算两个字符串之间的字面相似度。在使用字符串表示（也叫符号表示）计算文本的语义信息时，往往需要使用基于规则的方法。例如，要判断一个句子的情感极性（褒义或贬义），规则的形式可能为：如果句子中出现“喜欢”“漂亮”等词则为褒义；如果出现“讨厌”“丑陋”等词则为贬义。这种基于规则的方法存在很多问题。首先，规则的归纳依赖专家的经验，需要花费大量的人力、物力和财力；其次，规则的表达能力有限，很多语言现象无法用简单的规则描述；最后，随着规则的增多，规则之间可能存在矛盾和冲突的情况，导致最终无法做出决策。例如，一个句子中既出现了“喜欢”，又出现了“讨厌”的情况。

为了解决基于规则的方法存在的以上诸多问题，基于机器学习的自然语言处理技术应运而生，其最本质的思想是将文本表示为向量，其中的每一维代表一个特征。在进行决策的时候，只要对这些特征的相应值进行加权求和，就可以得到一个分数用于最终的判断。仍然以情感极性识别为例，一种非常简单的将原始文本表示为向量的方法为：令向量$x$的每一维表示某个词在该文本中出现的次数，如$x_1$表示“我”出现的次数，$x_2$表示“喜欢”出现的次数，$x_3$表示“电影”出现的次数，$x_4$表示“讨厌”出现的次数等，如果某个词在该句中没有出现，则相应的维数被设置为0。可见，输入向量$x$的大小恰好为整个词表所有不相同的词的大小。然后就可以根据每个词对判断情感极性的重要性进行加权，如“喜欢”（$x_2$）对应的权重$w_2$可能比较大，而“讨厌”（$x_4$）对应的权重$w_4$可能比较小（可以为负数），对于情感极性影响比较小的词，如“我”“电影”等，对应的权重可能会趋近于0。这种文本表示的方法是两种技术的组合，即词的独热表示和文本的词袋表示。除了可以应用于基于机器学习的方法，文本向量表示还可以用于计算两个文本之间的相似度，即使用余弦函数等度量函数表示两个向量之间的相似度，并应用于信息检索等任务。下面就以上提到的各项技术分别进行详细的介绍。

词的独热（One-hot）表示

所谓词的独热表示，即使用一个词表大小的向量表示一个词（假设词表为$V$，则其大小为$|V|$），然后将词表中的第$i$个词$w_i$表示为向量：
e w i = [ 0 , 0 , ⋯   , 1 ⏟ 第 i 个 , ⋯   , 0 ] ∈ { 0 , 1 } ∣ V ∣ e_{w_i} = [0, 0, \cdots, \underbrace{1}_{第i个}, \cdots, 0] \in \{0, 1\}^{|V|} ewi​​=[0,0,⋯,第i个 1​​,⋯,0]∈{0,1}∣V∣

在该向量中，词表中第$i$个词在第$i$维上被设置为1，其余维均为0。这种表示被称为词的独热表示或独热编码（One-hot Encoding）。独热表示的一个主要问题就是不同词使用完全不同的向量进行表示，这会导致即使两个词在语义上很相似，但是通过余弦函数来度量它们之间的相似度时值却为0。另外，当应用于基于机器学习的方法时，独热模型会导致数据稀疏（Data Sparsity）问题。例如，假设在训练数据中只见过“漂亮”，在测试数据中出现了“美丽”，虽然它们之间很相似，但是系统仍然无法恰当地对“美丽”进行加权。由于数据稀疏问题，导致当训练数据规模有限时，很多语言现象没有被充分地学习到。为了缓解数据稀疏问题，传统的做法是除了词自身，再提取更多和词相关的泛化特征，如词性特征、词义特征和词聚类特征等。以语义特征为例，通过引入WordNet等语义词典，可以获知“漂亮”和“美丽”是同义词，然后引入它们的共同语义信息作为新的额外特征，从而缓解同义词的独热表示不同的问题。可以说，在使用传统机器学习方法解决自然语言处理问题时，研究者的很大一部分精力都用在了挖掘有效的特征上。

词的分布式表示

词的独热表示容易导致数据稀疏问题，而通过引入特征的方法虽然可以缓解该问题，但是特征的设计费时费力。

分布式语义假设

人们在阅读过程中遇到从未见过的词时，通常会根据上下文来推断其含义以及相关属性。基于这种思想，John Rupert Firth于1957年提出了分布式语义假设：词的含义可由其上下文的分布进行表示。基于该思想，可以利用大规模的未标注文本数据，根据每个词的上下文分布对词进行表示。当然，分布式语义假设仅仅提供了一种语义建模的思想。具体到表示形式和上下文的选择，以及如何利用上下文的分布特征，都是需要解决的问题。下面用一个具体的例子演示如何构建词的分布式表示。假设语料库中有以下三句话：

我 喜欢 自然 语言 处理。
我 爱 深度 学习。
我 喜欢 机器 学习。

假设以词所在句子中的其他词语作为上下文，那么可以创建如下图所示的词语共现频次表。其中，词表$V$包含“我”、“喜欢”、…、“。”共10个词，即$|V|=10$。表中的每一项代表一个词$w_i$与另一个词$w_j$（上下文）在同一个句子中的共现频次，每个词与自身的共现频次设置为0。

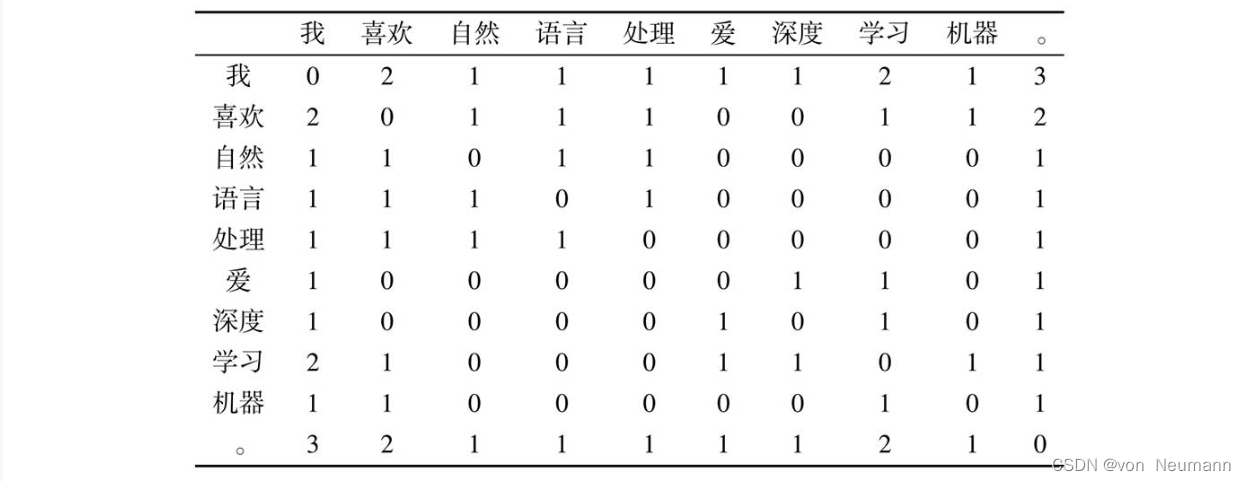
表中的每一行代表一个词的向量。通过计算两个向量之间的余弦函数，就可以计算两个词的相似度。如“喜欢”和“爱”，由于有共同的上下文“我”和“学习”，使得它们之间具有了一定的相似性，而不是如独热表示一样，没有任何关系。除了词，上下文的选择有很多种方式，而选择不同的上下文得到的词向量表示性质会有所不同。例如，可以使用词在句子中的一个固定窗口内的词作为其上下文，也可以使用所在的文档本身作为上下文。前者得到的词表示将更多地反映词的局部性质：具有相似词法、句法属性的词将会具有相似的向量表示。而后者将更多地反映词代表的主题信息。不过，直接使用与上下文的共现频次作为词的向量表示，至少存在以下三个问题：

• 高频词误导计算结果。如上例中，“我”和“。”与其他词的共现频次很高，导致实际上可能没有关系的两个词由于都和这些词共现过，从而产生了较高的相似度。
• 共现频次无法反映词之间的高阶关系。例如，假设词“A”与“B”共现过，“B”与“C”共现过，“C”与“D”共现过，通过共现频次，只能获知“A”与“C”都与“B”共现过，它们之间存在一定的关系，而“A”与“D”这种高阶的关系则无法知晓。
• 仍然存在稀疏性的问题。即向量中仍有大量的值为0，这一点从上图中也可以看出。

点互信息

首先看如何解决高频词误导计算结果的问题。最直接的想法是：如果一个词与很多词共现，则降低其权重；反之，如果一个词只与个别词共现，则提高其权重。信息论中的点互信息（Pointwise Mutual Information，PMI）恰好能够做到这一点。对于词$w$和上下文$c$，其PMI为：
$$\text{PMI}(w,c)={\log }_2\frac{P(w,c)}{P(w)P(c)}$$

式中，$P(w,c)$、$P(w)$和$P(c)$分别是$w$与$c$的共现概率，以及$w$和$c$分别出现的概率。可见，通过PMI公式计算，如果$w$和$c$的共现概率（与频次正相关）较高，但是$w$或者$c$出现的概率也较高（高频词），则最终的PMI值会变小；反之，即便$w$和$c$的共现概率不高，但是$w$或者$c$出现的概率较低（低频词），则最终的PMI值也可能会比较大。从而较好地解决高频词误导计算结果的问题。
$$\begin{array}{rl}P(w,c)& =\frac{C(w,c)}{{\sum }_{w^{\prime }}{\sum }_{c^{\prime }}C(w^{\prime },c^{\prime })}\\ P(w)& =\frac{C(w)}{{\sum }_{w^{\prime }}C(w^{\prime })}=\frac{{\sum }_{c^{\prime }}C(w,c^{\prime })}{{\sum }_{w^{\prime }}{\sum }_{c^{\prime }}C(w^{\prime },c^{\prime })}\\ P(c)& =\frac{C(c)}{{\sum }_{c^{\prime }}C(c^{\prime })}=\frac{{\sum }_{w^{\prime }}C(w^{\prime },c)}{{\sum }_{w^{\prime }}{\sum }_{c^{\prime }}C(w^{\prime },c^{\prime })}\end{array}$$

式中：$C(w,c)$表示词$w$和上下文$c$在语料库中出现的次数（也称为频次）；${\sum }_{c^{\prime }}C(w,c^{\prime })$为上图按行求和；${\sum }_{w^{\prime }}C(w^{\prime },c)$为上图按列求和；${\sum }_{w^{\prime }}{\sum }_{c^{\prime }}C(w^{\prime },c^{\prime })$为全部共现频次的和。代入以上3个公式，可以进一步写为：
$$\begin{array}{rl}\text{PMI}(w,c)& ={\log }_2\frac{P(w,c)}{P(w)P(c)}\\ & ={\log }_2\frac{C(w,c)}{\frac{{\sum }_{c^{\prime }}C(w,c^{\prime }){\sum }_{w^{\prime }}C(w^{\prime },c)}{{\sum }_{w^{\prime }}{\sum }_{c^{\prime }}C(w^{\prime },c^{\prime })}}\end{array}$$

另外，当某个词与上下文之间共现次数较低时，可能会得到负的PMI值。考虑到这种情况下的PMI不太稳定（具有较大的方差），在实际应用中通常采用PPMI （Positive PMI）的形式，即：
$$\text{PPMI}=\max (\text{PMI}(w,c),0)$$

接下来介绍PMI的代码实现。首先，将类似上图形式的共现频次表定义为共现矩阵的形式，即$M\in R^{|V|\times |C|}$，其中$V$为词表，$C$为全部的上下文，$M_{ij}$为词$w_i$与上下文$c_j$在语料库中的共现频次。然后，编写如下代码计算PPMI：

import numpy as np
M = np.array([[0, 2, 1, 1, 1, 1, 1, 2, 1, 2], 
              [2, 0, 1, 1, 1, 0, 0, 1, 1, 2], 
              [1, 1, 0, 1, 1, 0, 0, 0, 0, 1], 
              [1, 1, 1, 1, 0, 0, 0, 0, 0, 1], 
              [1, 1, 1, 1, 0, 0, 0, 0, 0, 1], 
              [1, 0, 0, 0, 0, 0, 1, 1, 0, 1], 
              [1, 0, 0, 0, 0, 1, 0, 1, 0, 1], 
              [2, 1, 0, 0, 0, 1, 1, 0, 1, 1], 
              [1, 1, 0, 0, 0, 0, 0, 1, 0, 1],
              [3, 2, 1, 1, 1, 1, 1, 2, 1, 0]])
              
def pmi(M, positive=True):
    col_totals = M.sum(axis=0)
    row_totals = M.sum(axis=1)
    total = col_totals.sum()
    expected = np.outer(row_totals, col_totals) / total
    M = M / expected
    with np.errstate(divide='ignore'):
        M = np.log(M)
    
    M[np.isinf(M)] = 0.0
    if positive:
        M[M < 0] = 0.0
    return M

pmi(M)

奇异值分解

奇异值分解（Singular Value Decomposition，SVD）是一种解决共现频次无法反映词之间高阶关系问题的常见做法。对共现矩阵$M$进行奇异值分解：
$$M=U\Sigma V^T$$

其中，$U\in R^{|V|\times r}$，$V\in R^{r\times |C|}$为正交矩阵，满足$U^{T}U=V^{T}V=I$；$\Sigma \in R^{r\times r}$是由$r$个奇异值（Singular Value）构成的对角矩阵。若在$\Sigma$中仅保留$d$个（$d＜r$）最大的奇异值（$U$和$V$也只保留相应的维度），则被称为截断奇异值分解（Truncated Singular Value Decomposition）。截断奇异值分解实际上是对矩阵$M$的低秩近似。通过截断奇异值分解所得到的矩阵$U$中的每一行，则为相应词的$d$维向量表示，该向量一般具有连续、低维和稠密的性质。由于$U$的各列相互正交，因此可以认为词表示的每一维表达了该词的一种独立的“潜在语义”，所以这种方法也被称作潜在语义分析（Latent Semantic Analysis，LSA）。相应地，$\Sigma V^T$的每一列也可以作为相应上下文的向量表示。

在Python的numpy.linalg库中内置了SVD函数，只需要输入共现矩阵，然后调用相应的函数即可。如：

M_pmi = pmi(M)
U, s, vh = np.linalg.svd(M_pmi)

在信息检索等领域，也经常通过词与其出现的文档构成“词–文档”共现矩阵，此时也可以通过上文介绍的奇异值分解技术进行降维，并在低维空间（潜在语义空间）内计算词语或者文档之间的相似度，该技术也称潜在语义索引（Latent Semantic Indexing，LSI）。虽然在基于传统机器学习的方法中，词的分布式表示取得了不错的效果，但是其仍然存在一些问题。首先，当共现矩阵规模较大时，奇异值分解的运行速度非常慢；其次，如果想在原来语料库的基础上增加更多的数据，则需要重新运行奇异值分解算法，代价非常高；另外，分布式表示只能用于表示比较短的单元，如词或短语等，如果待表示的单元比较长，如段落、句子等，由于与其共现的上下文会非常少，则无法获得有效的分布式表示；最后，分布式表示一旦训练完成，则无法修改，也就是说，无法根据具体的任务调整其表示方式。为

词嵌入表示（Word Embedding）

与词的分布式表示类似，词嵌入表示（Word Embedding）也使用一个连续、低维、稠密的向量来表示词，经常直接简称为词向量，但与分布式表示不同之处在于其赋值方式。在词的分布式表示中，向量值是通过对语料库进行统计得到的，然后再经过点互信息、奇异值分解等变换，一旦确定则无法修改。而词向量中的向量值，是随着目标任务的优化过程自动调整的，也就是说，可以将词向量中的向量值看作模型的参数。不过，如果目标任务的训练数据比较少，学习合适的词向量难度会比较大，因此，利用自然语言文本中所蕴含的自监督学习信号（即词与上下文的共现信息），先来预训练词向量，往往会获得更好的结果。

文本的词袋表示

上文介绍了几种常见的词表示方法，那么如何通过词的表示构成更长文本的表示呢？在此介绍一种最简单的文本表示方法——词袋（Bag-Of-Words，BOW）表示。所谓词袋表示，就是假设文本中的词语是没有顺序的集合，将文本中的全部词所对应的向量表示（既可以是独热表示，也可以是分布式表示或词向量）相加，即构成了文本的向量表示。如在使用独热表示时，文本向量表示的每一维恰好是相应的词在文本中出现的次数。虽然这种文本表示的方法非常简单、直观，但是其缺点也非常明显：首先是没有考虑词的顺序信息，导致“张三打李四”和“李四打张三”，虽然含义不同，但是由于它们包含的词相同，即使词序不同，词袋表示的结果也是一样的；其次是无法融入上下文信息。比如要表示“不喜欢”，只能将两个词的向量相加，无法进行更细致的语义操作。当然，可以通过增加词表的方法加以解决，比如引入二元词（Bigram）词表，将“不+喜欢”等作为“词”，然后同时学习二元词的词向量表示。这种方法既能部分解决否定词的问题，也能部分解决局部词序的问题，但是随着词表的增大，会引入更严重的数据稀疏问题。深度学习技术的引入为解决这些问题提供了更好的方案

参考文献：
[1] 车万翔, 崔一鸣, 郭江. 自然语言处理：基于预训练模型的方法[M]. 电子工业出版社, 2021.
[2] 邵浩, 刘一烽. 预训练语言模型[M]. 电子工业出版社, 2021.
[3] 何晗. 自然语言处理入门[M]. 人民邮电出版社, 2019
[4] Sudharsan Ravichandiran. BERT基础教程：Transformer大模型实战[M]. 人民邮电出版社, 2023
[5] 吴茂贵, 王红星. 深入浅出Embedding：原理解析与应用实战[M]. 机械工业出版社, 2021.