前言

int8的数据范围可以表示为-128到127之间的整数
uint8的数据范围可以表示为0到255之间的整数
注释：int8就是用8个比特位来保存整数，第一位用来表示符号。uint8表示无符号整数，没有符号位，8个比特位全部用来表示整数。

1.问题

1.1 引出问题

截断的数值最后反量化与原数值相差较大(1.62与1.1062843)，如何解决该问题？
方法一：偏移–非对称量化
方法第二：最大绝对值对称法–对称量化

1.2 非对称量化

原理分析

动态范围量化(Dynamic Range Quantization)中的校准过程(Calibration)。它属于非对称量化的一种形式。由于量化参数(比如量化因子Scale)是通过数据集的统计量来估计的，因此称之为动态范围量化。它能够减少量化误差的原因是，引入了一个偏移量Z，使得量化后的数值在更小的范围内，进而减小量化误差。同时，偏移量Z的计算使得量化后的最大值Rmax落在了Qmax上，保证了最大值的精度。

动态范围量化

通过引入偏移量Z可以解决。具体公式如下：
在这里插入图片描述
其中，为什么偏移量Z的公式是这样定义呢？
可以看TensorRT量化第二课：对称量化与非对称量化的2.3.2 偏移量Z

代码

import numpy as np

def saturete(x, int_max, int_min):
    return np.clip(x, int_min, int_max)

def scale_z_cal(x, int_max, int_min):
    scale = (x.max() - x.min()) / (int_max - int_min)
    z = int_max - np.round((x.max() / scale))
    return scale, z

def quant_float_data(x, scale, z, int_max, int_min):
    xq = saturete(np.round(x/scale + z), int_max, int_min)
    return xq

def dequant_data(xq, scale, z):
    x = ((xq - z)*scale).astype('float32')
    return x

if __name__ == "__main__":
    np.random.seed(1)
    data_float32 = np.random.randn(3).astype('float32')
    int_max = 127
    int_min = -128
    print(f"input = {data_float32}")

    scale, z = scale_z_cal(data_float32, int_max, int_min)
    print(f"scale = {scale}")
    print(f"z = {z}")
    data_int8 = quant_float_data(data_float32, scale, z, int_max, int_min)
    print(f"quant_result = {data_int8}")
    data_dequant_float = dequant_data(data_int8, scale, z)
    print(f"dequant_result = {data_dequant_float}")
    
    print(f"diff = {data_dequant_float - data_float32}")

输出如下：

input = [ 1.6243454 -0.6117564 -0.5281718]
scale = 0.008769026924582089
z = -58.0
quant_result = [ 127. -128. -118.]
dequant_result = [ 1.62227    -0.6138319  -0.52614164]
diff = [-0.00207543 -0.00207549  0.00203013]

首先输入数组不变为[ 1.6243454 -0.6117564 -0.5281718]，还是需要将其量化到int8范围即[-128 127]，scale还是0.008769，z根据公式计算为-58，量化后的结果为[127 -128 -118]，反量化后的结果为[ 1.62227 -0.6138319 -0.52614164]，偏差为[-0.00207543 -0.00207549 0.00203013]，可以看到加入了Z偏移量后的误差明显减小了。

通过引入偏移量Z，我们可以将量化后的数值范围向中心偏移，从而在整个量化数值范围内分布得更加均匀，减小了误差得积累。虽然最终仍然会有截断操作，但是这种偏移可以在整个数值分布上起到更好得平衡作用，从而减小了误差的影响。

1.3 对称量化

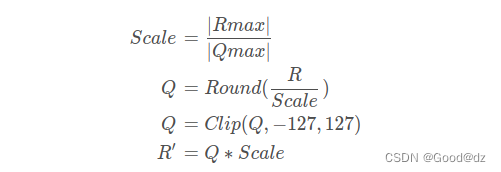
代码

import numpy as np

def saturete(x):
    return np.clip(x, -127, 127)

def scale_cal(x):
    max_val = np.max(np.abs(x))
    return max_val / 127

def quant_float_data(x, scale):
    xq = saturete(np.round(x/scale))
    return xq

def dequant_data(xq, scale):
    x = (xq * scale).astype('float32')
    return x

if __name__ == "__main__":
    np.random.seed(1)
    data_float32 = np.random.randn(3).astype('float32')
    print(f"input = {data_float32}")

    scale = scale_cal(data_float32)
    print(f"scale = {scale}")

    data_int8 = quant_float_data(data_float32, scale)
    print(f"quant_result = {data_int8}")
    data_dequant_float = dequant_data(data_int8, scale)
    print(f"dequant_result = {data_dequant_float}")

    print(f"diff = {data_dequant_float - data_float32}")

输出如下：

input = [ 1.6243454 -0.6117564 -0.5281718]
scale = 0.012790121431425801
quant_result = [127. -48. -41.]
dequant_result = [ 1.6243454 -0.6139258 -0.524395 ]   
diff = [ 0.         -0.00216943  0.00377679]

对称量化方法不用计算偏移量Z，计算量小，是一种非饱和量化。在对称量化中还存在一个问题，比如目前原始数组中有1000个点分布在[-1,1]之间，突然有个离散点分布在100处，此时做对称量化时Scale会被调整得很大，使得上下限超出[-127,127]的范围，从而导致量化误差增大，对精度的影响也会相应增大。

因此，在对称量化中，需要谨慎处理数据中的极端值，以免对量化精度造成不利影响。因此，需要动态选择范围来去除离散点，让max的选取更加的合理。