总体思路
磁力计的数据在实际中是椭球的形状,在此之前使用了球体拟合进行校准,也就是简化为正球体的模型,得出的结果比较差,航向计算不准,还是需要用椭球的模型来估计偏移量,先使用标准的椭球方程,进行化简与变形,得到最小二乘法可以进行估计的标准形式,之后对原始数据进行最小二乘法矩阵的赋值,求解方程,最终观察拟合效果。
椭球方程
椭球的标准方程为:
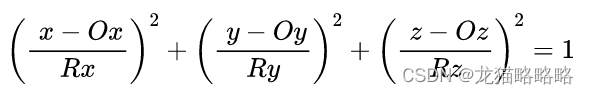
最小二乘法原理回顾
在这里由于数据是一次性采集完之后处理,因此使用批处理最小二乘法即可,批处理最小二乘法的原理简单来说就是如下的过程:
对于一组采用数据,当前有:
1)数据向量:φ = [x1 x2 ... xn]T
2) 输出向量:y
3) 参数矩阵:θ = [a1 a2 ... an]T
对于单组数据:
实际输出为:y = φT * θ
估计输出就为:y_hat = φT * θ_hat
对于多组采样数据,将单组数据向量集合起来写成矩阵的形式,为:

引入一个估计误差的变量,记作 e:

之后可以根据误差 e,写出最小二乘的指标函数 J:
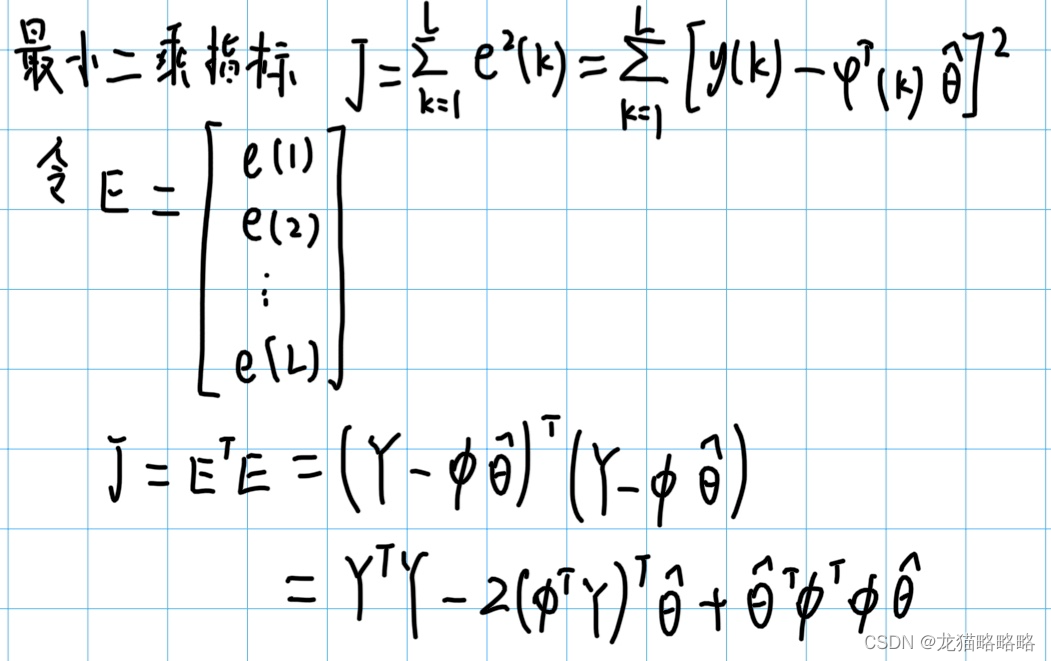
对 J 求导,便可以得到估计参数 θ_hat 的极值,进而写出估计参数 θ_hat 的表达式:

椭球方程化简
椭球方程化简,就是将椭球方程转化为适合最小二乘法求解的形式,先将椭球方程展开,得到:
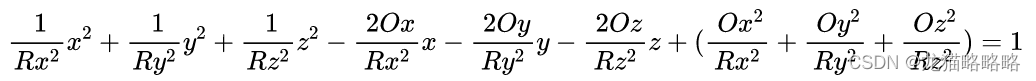
最初也是直接使用的此方程进行最小二乘法拟合的,也就是输出矩阵 Y 都是 1 的形式。但使用此方程会有问题,可以求出多个解,使用matlab求解的话,很容易就会求出异常的解,也就是Rx,Ry,Rz很大的时候,也是会满足方程的,但这个解肯定是不对的。
因此需要对此方程进行变种,在查找了网上其他人的做法后,比较好的做法是两边同时乘上 Rx2 ,之后,将 x2 移到等式右边:
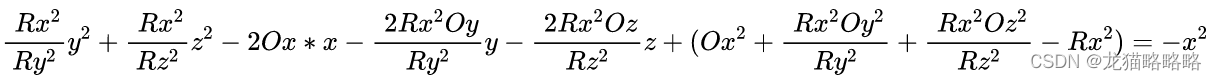
以上述方程建立最小二乘法需要的矩阵:
数据向量:φ = [y2 z2 x y z 1]T
输出向量:y = -x2
参数矩阵:θ = [(Rx2/Ry2) (Rx2/Rz2) (-2Ox) (-2Rx2Oy/Ry2) (-2Rx2Oz/Rz2) (Ox2+Rx2Oy/Ry2+Rx2Oz/Rz2-Rx2)]T
之后再把单个采样的向量集合起来写成矩阵的形式:

之后就可以求解出估计参数矩阵 θ_hat,进而就可以求解出椭球的三轴中心 Ox,Oy,Oz,以及半轴长 Rx,Ry,Rz:
Ox = -theta_hat(3) / 2;
Oy = -theta_hat(4) / (2*theta_hat(1));
Oz = -theta_hat(5) / (2*theta_hat(2));
Rx = sqrt(Ox*Ox + theta_hat(1)*Oy*Oy + theta_hat(2)*Oz*Oz - theta_hat(6));
Ry = sqrt((Rx*Rx) / theta_hat(1));
Rz = sqrt((Rx*Rx) / theta_hat(2));
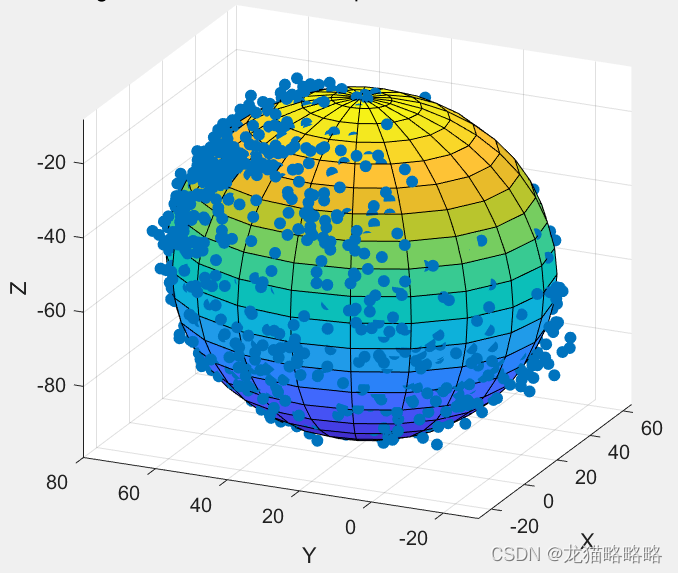
原始采样的磁力计数据图:
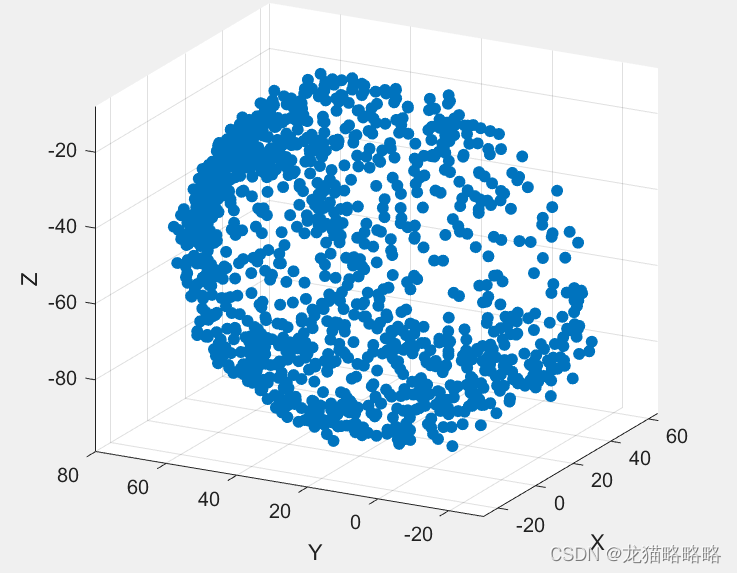
加上拟合的椭球模型: