1 理论基础
PID控制器应用广泛,其一般形式为

可见,PID控制器的性能取决于Kp、Ki、Kd这3个参数是否合理,因此,优化PID控制器参数具有重要意义。目前,PID控制器参数主要是人工调整,这种方法不仅费时,而且不能保证获得最佳的性能。PSO已经广泛应用于函数优化、神经网络训练、模式分类、模糊系统控制以及其他应用领域,本案例将使用PSO进行PID控制器参数的优化设计。
2 案例背景
2.1 问题描述
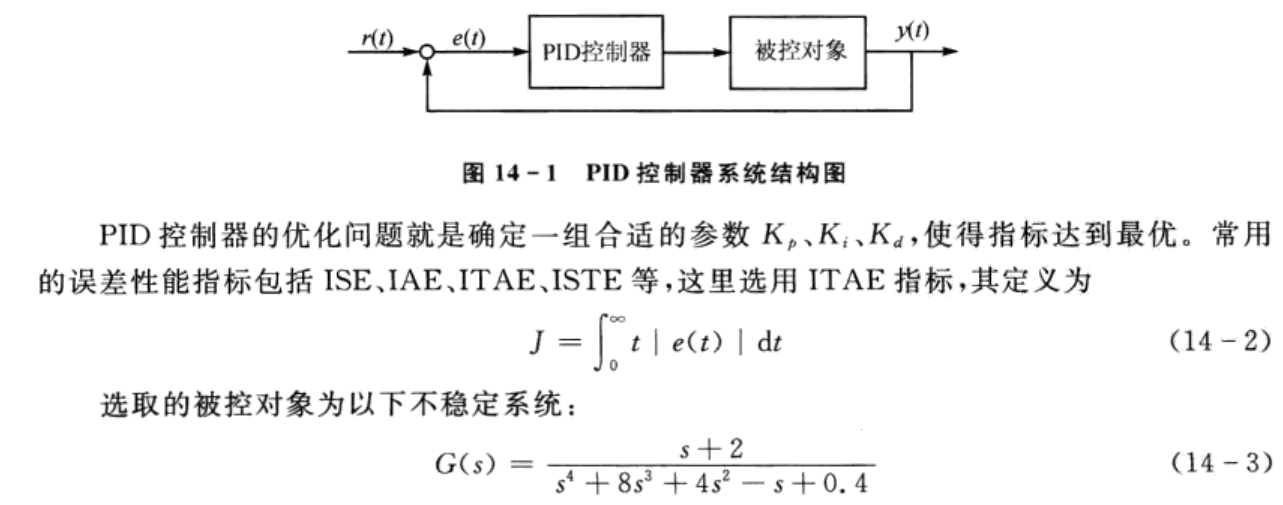
PID控制器的系统结构图如图14-1所示。
在Simulink环境下建立的模型如图14-2所示。

图14-2中,微分环节由一个一阶环节近似,输出端口1即为式(14-2)所示的ITAE指标,通过将时间及误差绝对值的乘积进行积分后得到。
2.2 解题思路及步骤
1.优化设计过程
利用粒子群算法对PID控制器的参数进行优化设计,其过程如图14-3所示。
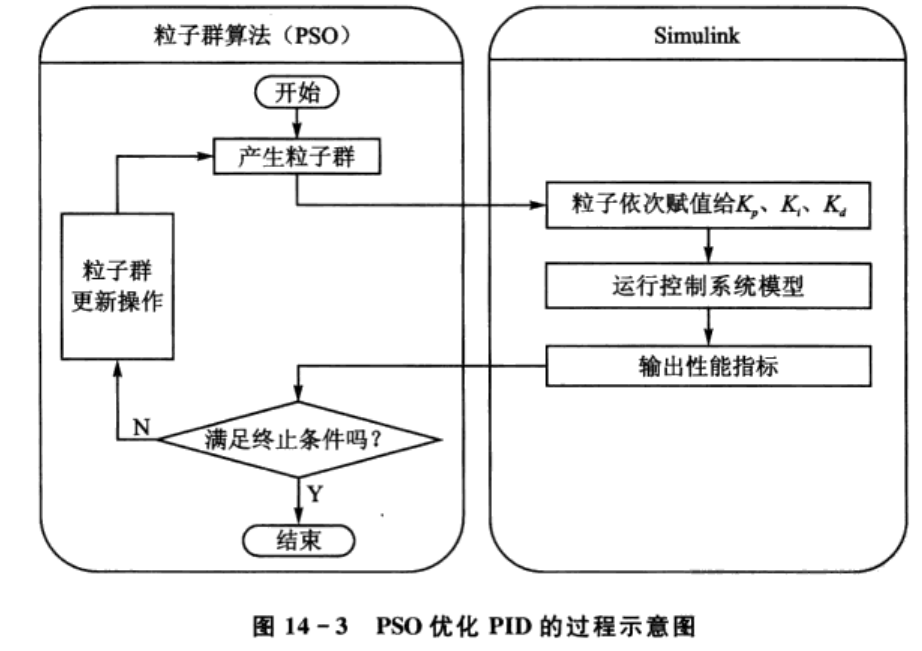
图14-3中,粒子群算法与Simulink模型之间连接的桥梁是粒子(即PID控制器参数)和该粒子对应的适应值(即控制系统的性能指标)。优化过程如下:PSO产生粒子群(可以是初始化粒子群,也可以是更新后的粒子群),将该粒子群中的粒子依次赋值给PID控制器的参数Kp、Ki、Kd,然后运行控制系统的Simulink模型,得到该组参数对应的性能指标,该性能指标传递到PSO中作为该粒子的适应值,最后判断是否可以退出算法。
2.粒子群算法实现
粒子群算法的基本原理在前面已经述及,进一步地,粒子在搜索空间中的速度和位置根据以下公式确定:
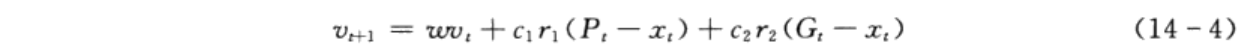

PSO的流程如下:
(1)初始化粒子群,随机产生所有粒子的位置和速度,并确定粒子的Pt和Gt。
(2)对每个粒子,将其适应值与该粒子所经历过的最优位置P,的适应值进行比较,如较好,则将其作为当前的Pt。
(3)对每个粒子,将其适应值与整个粒子群所经历过的最优位置Gt的适应值进行比较,如较好,则将其作为当前的Gt。
(4)按式(14-4)和式(14-5)更新粒子的速度和位置。
(5)如果没有满足终止条件(通常为预设的最大迭代次数和适应值下限值),则返回步骤(2);否则,退出算法,得到最优解。
3 MATLAB程序实现
3.1 Simulink部分的程序实现
图14-3所示的PSO优化PID过程示意图,其右侧的Simulink部分的程序实现如下:
function z=PSO_PID(x)
assignin('base','Kp',x(1));
assignin('base','Ki',x(2));
assignin('base','Kd',x(3));
[t_time,x_state,y_out]=sim('PID_Model',[0,20]);
z=y_out(end,1);
其中,x为PSO中传递过来的粒子,首先,调用函数assignin将x(1)、x(2)、x(3)的值赋值给Workspace中的Kp、Ki、Kd,该语句实现了图14-3中从PSO部分到Simulink部分的参数传递;然后,调用函数sim对图14-2所示的模型进行仿真,其中,PID_Model为Simulink模型的文件名,[0,20]为仿真时间,返回的y_out即为输出端子1的值;最后,将性能指标ITAE赋值给z,以实现图14-3中从Simulink部分到PSO部分的参数传递。
3.2 PSO部分的程序实现
设置PSO的参数为:惯性因子w=0.6,加速常数c?=c?=2,维数为3(有3个待优化参数),粒子群规模为100,待优化函数为14.3.1节中的函数PSO_PID,最大迭代次数为100,最小适应值为0.1,速度范围为[-1,1],3个待优化参数范围均为[0,300]。代码如下:
%% 清空环境
clear
clc
%% 参数设置
w = 0.6; % 惯性因子
c1 = 2; % 加速常数
c2 = 2; % 加速常数
Dim = 3; % 维数
SwarmSize = 100; % 粒子群规模
ObjFun = @PSO_PID; % 待优化函数句柄
MaxIter = 100; % 最大迭代次数
MinFit = 0.1; % 最小适应值
Vmax = 1;
Vmin = -1;
Ub = [300 300 300];
Lb = [0 0 0];
%% 粒子群初始化
Range = ones(SwarmSize,1)*(Ub-Lb);
Swarm = rand(SwarmSize,Dim).*Range + ones(SwarmSize,1)*Lb % 初始化粒子群
VStep = rand(SwarmSize,Dim)*(Vmax-Vmin) + Vmin % 初始化速度
fSwarm = zeros(SwarmSize,1);
for i=1:SwarmSize
fSwarm(i,:) = feval(ObjFun,Swarm(i,:)); % 粒子群的适应值
end
%% 个体极值和群体极值
[bestf bestindex]=min(fSwarm);
zbest=Swarm(bestindex,:); % 全局最佳
gbest=Swarm; % 个体最佳
fgbest=fSwarm; % 个体最佳适应值
fzbest=bestf; % 全局最佳适应值
%% 迭代寻优
iter = 0;
y_fitness = zeros(1,MaxIter); % 预先产生4个空矩阵
K_p = zeros(1,MaxIter);
K_i = zeros(1,MaxIter);
K_d = zeros(1,MaxIter);
while( (iter < MaxIter) && (fzbest > MinFit) )
for j=1:SwarmSize
% 速度更新
VStep(j,:) = w*VStep(j,:) + c1*rand*(gbest(j,:) - Swarm(j,:)) + c2*rand*(zbest - Swarm(j,:));
if VStep(j,:)>Vmax, VStep(j,:)=Vmax; end
if VStep(j,:)<Vmin, VStep(j,:)=Vmin; end
% 位置更新
Swarm(j,:)=Swarm(j,:)+VStep(j,:);
for k=1:Dim
if Swarm(j,k)>Ub(k), Swarm(j,k)=Ub(k); end
if Swarm(j,k)<Lb(k), Swarm(j,k)=Lb(k); end
end
% 适应值
fSwarm(j,:) = feval(ObjFun,Swarm(j,:));
% 个体最优更新
if fSwarm(j) < fgbest(j)
gbest(j,:) = Swarm(j,:);
fgbest(j) = fSwarm(j);
end
% 群体最优更新
if fSwarm(j) < fzbest
zbest = Swarm(j,:);
fzbest = fSwarm(j);
end
end
iter = iter+1; % 迭代次数更新
y_fitness(1,iter) = fzbest; % 为绘图做准备
K_p(1,iter) = zbest(1);
K_i(1,iter) = zbest(2);
K_d(1,iter) = zbest(3);
end
%% 绘图输出
figure(1) % 绘制性能指标ITAE的变化曲线
plot(y_fitness,'LineWidth',2)
title('最优个体适应值','fontsize',18);
xlabel('迭代次数','fontsize',18);ylabel('适应值','fontsize',18);
set(gca,'Fontsize',18);
figure(2) % 绘制PID控制器参数变化曲线
plot(K_p)
hold on
plot(K_i,'k','LineWidth',3)
plot(K_d,'--r')
title('Kp、Ki、Kd 优化曲线','fontsize',18);
xlabel('迭代次数','fontsize',18);ylabel('参数值','fontsize',18);
set(gca,'Fontsize',18);
legend('Kp','Ki','Kd',1);
其中,MaxIter和MinFit即终止条件;Vmax和Vmin分别为速度的上限和下限;Ub(i)和Lb(i)分别为第i个待优化参数的上限和下限。粒子群的初始化采用与遗传算法相似的方法(用函数rand且保证粒子在上下限范围内),迭代过程采用while进行大循环,速度更新和位置更新按照式 (14-4)和式(14-5)进行(且在迭代 更新过程中,若超出了限值,则将其 设为限制)。
3.3 结果分析
运行以上代码,得到优化过程如图14-4和图14-5所示,前者为PID控制器3个参数Ki、Kp、Kd的变化曲线,后者为性能指标ITAE的变化曲线。得到的最优控制器参数及性能指标为
Kp= 33.6469,Ki=0.1662, Kd=38.7990, ITAE =1.0580
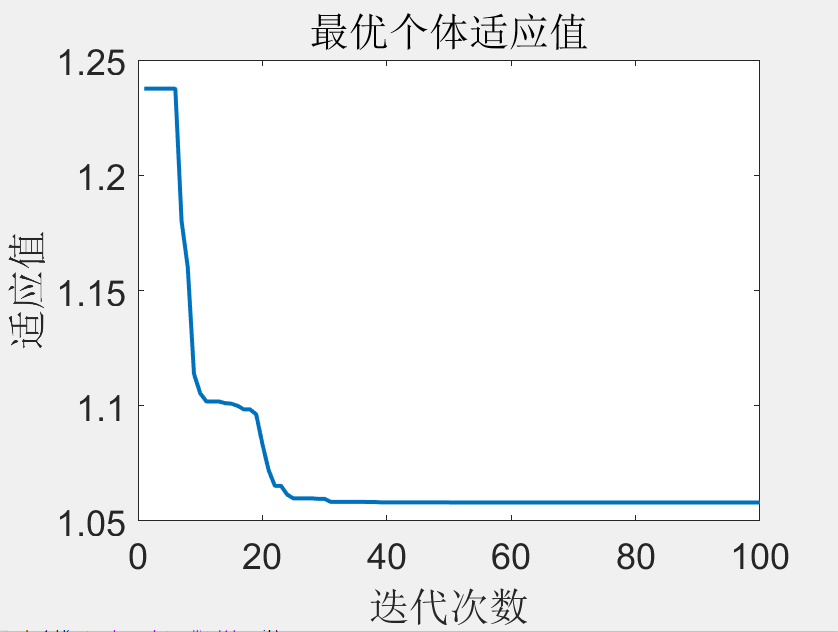
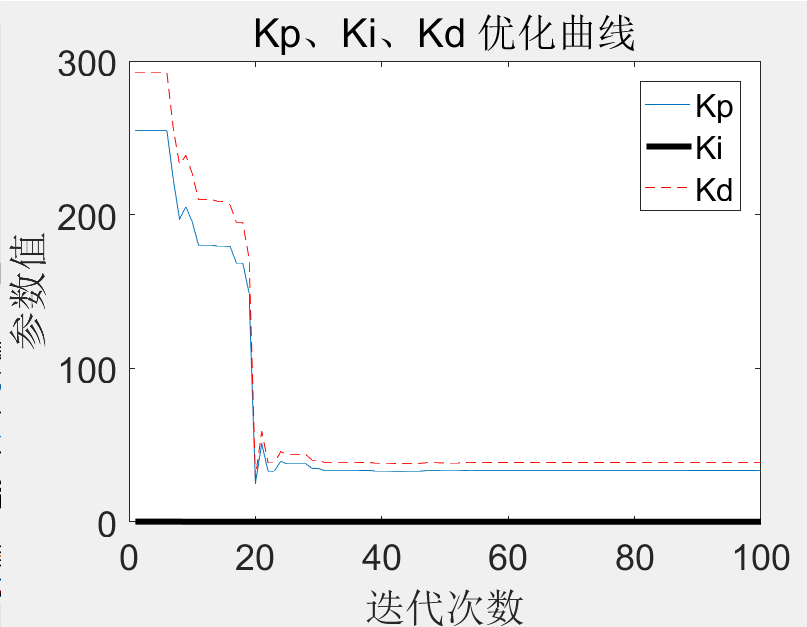
将以上参数代回图14-2所示的模型,得到的单位阶跃响应曲线如图14-6所示。由图14-5可知,算法优化过程中,性能指标ITAE不断减小,PSO不断寻找更优的参数。