作者：CSDN @ _养乐多_

本文将介绍使用python语言绘制广义线性模型（Generalized Additive Model，GAM）非线性回归散点图和拟合曲线。并记录了计算RMSE、ubRMSE、R2、Bias的代码。

---

---

一、GAM非线性回归详解

GAM（Generalized Additive Model）是一种用于非线性回归和分类的灵活的统计模型。它是广义线性模型（GLM）的扩展，可以对各种类型的非线性关系进行建模。

在 GAM 中，目标变量被假设为由一组平滑函数的线性组合和一个可能的链接函数组成。这些平滑函数可以捕捉到自变量与因变量之间的非线性关系。通过将每个自变量与一个或多个平滑函数相关联，GAM 可以灵活地建模各种非线性关系。

GAM 的一般形式可以表示为：

$$y=f1(x1)+f2(x2)+...+fp(xp)+\epsilon$$
其中，y 是目标变量，x1, x2, …, xp 是自变量，f1, f2, …, fp 是平滑函数，ε 是误差项。

在 GAM 中，常用的平滑函数有样条函数（spline function）、自然样条函数（natural spline function）、局部样条函数（local spline function）等。这些平滑函数可以对数据进行光滑处理，从而更好地捕捉变量之间的非线性关系。

GAM 的建模过程通常涉及以下步骤：

1. 准备数据：包括获取自变量和目标变量的数据，并进行必要的数据预处理。

2. 选择平滑函数：根据自变量的特点和非线性关系的假设，选择适当的平滑函数。常用的选择包括样条函数、自然样条函数等。

3. 拟合 GAM 模型：将自变量和平滑函数结合，拟合 GAM 模型。拟合过程可以使用最小二乘估计、广义最小二乘估计等方法进行。

4. 模型评估：评估拟合的 GAM 模型的性能，包括检查模型的拟合优度、残差分析等。

5. 预测和推断：使用训练好的 GAM 模型进行预测，并进行推断分析。

GAM 具有许多优点，包括：

• 灵活性：GAM 可以灵活地建模各种非线性关系，适用于各种复杂的数据模式。

• 可解释性：由于每个自变量与一个平滑函数相关联，GAM 的结果可以很好地解释自变量与目标变量之间的关系。

• 鲁棒性：GAM 对异常值和噪声具有一定的鲁棒性。

• 自动特征选择：GAM 可以通过平滑函数的选择来自动选择与目标变量相关的自变量。

然而，GAM 也存在一些限制和注意事项：

• 平滑函数的选择：选择适当的平滑函数是关键步骤之一，需要根据数据的特点和研究问题进行合理选择。

• 多重比较问题：在使用多个平滑函数进行建模时，需要进行多重比较校正，以避免估计的平滑函数数量过多导致的误差增加。

• 计算复杂度：与线性模型相比，GAM 的计算复杂度较高，特别是在处理大规模数据集时。

总体而言，GAM 是一种强大的非线性建模工具，可以帮助我们更好地理解数据中的非线性关系。通过合理选择平滑函数并进行适当的模型评估，可以在实际问题中应用 GAM 进行预测和推断分析。

二、代码

import numpy as np
import matplotlib.pyplot as plt
from pygam import LinearGAM, s, f


# 生成模拟数据
np.random.seed(42)
n = 100
X = np.linspace(0, 10, n)
y = np.sin(X) + np.random.normal(0, 0.1, n)


# 拟合 GAM 模型
gam = LinearGAM(s(0)).fit(X, y)


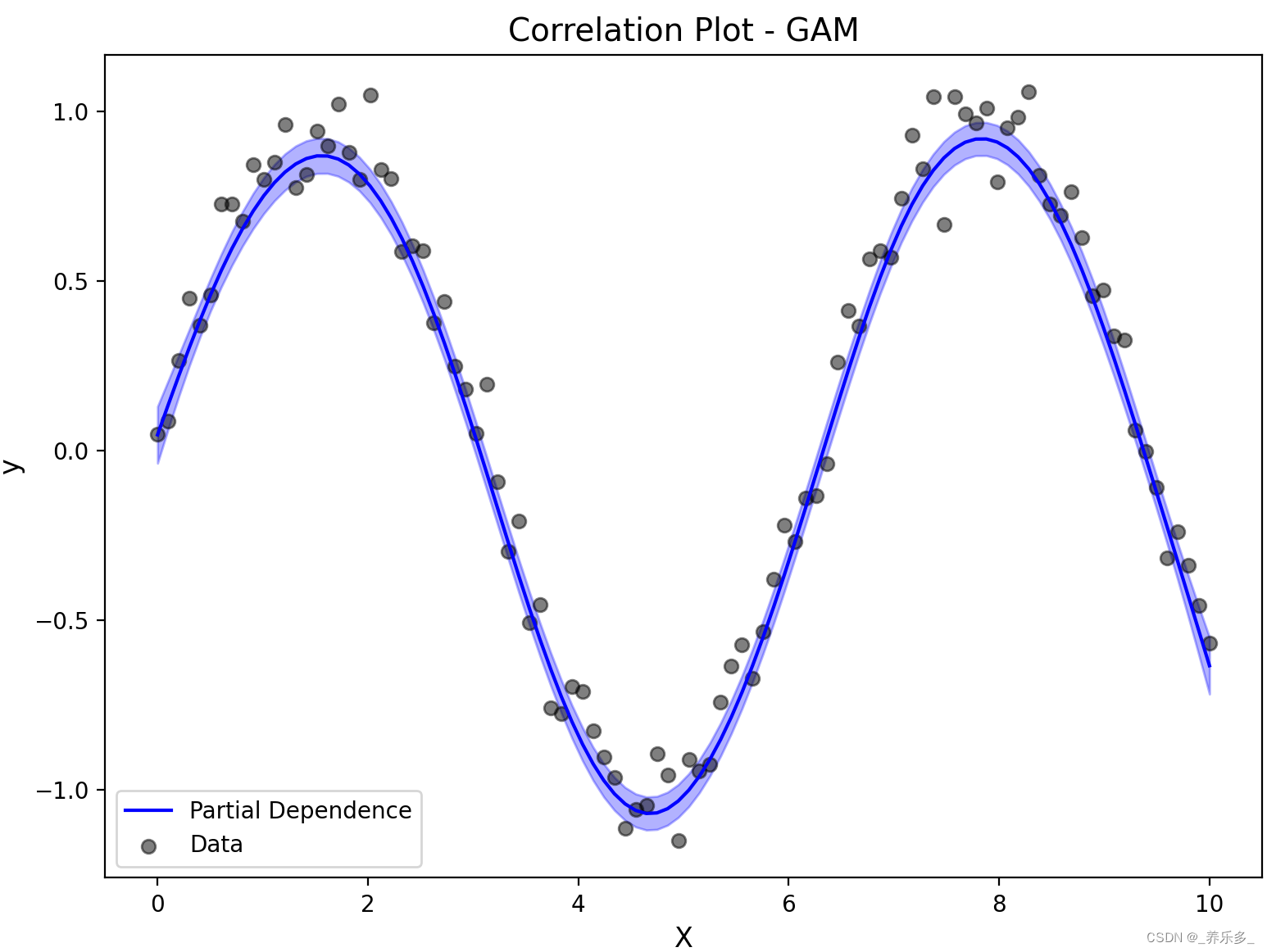
# 绘制相关性图
fig, axs = plt.subplots(1, 1, figsize=(8, 6))
XX = gam.generate_X_grid(term=0, n=100)
pdep, confi = gam.partial_dependence(term=0, X=XX, width=0.95)
axs.plot(XX[:, 0], pdep, color='blue', label='Partial Dependence')
axs.fill_between(XX[:, 0], confi[:, 0], confi[:, 1], color='blue', alpha=0.3)
axs.scatter(X, y, color='black', alpha=0.5, label='Data')
axs.set_xlabel('X', fontsize=12)
axs.set_ylabel('y', fontsize=12)
axs.set_title('Correlation Plot - GAM', fontsize=14)
axs.legend()

plt.tight_layout()
plt.show()

三、计算RMSE、ubRMSE、R2、Bias

import numpy as np
import matplotlib.pyplot as plt
from pygam import LinearGAM, s, f
from sklearn.metrics import mean_squared_error, r2_score
from scipy.stats import linregress


# 生成模拟数据
np.random.seed(42)
n = 100
X = np.linspace(0, 10, n)
y = np.sin(X) + np.random.normal(0, 0.1, n)

# 拟合 GAM 模型
gam = LinearGAM(s(0)).fit(X, y)

# 绘制相关性图
fig, axs = plt.subplots(1, 1, figsize=(8, 6))
XX = gam.generate_X_grid(term=0, n=100).flatten()
print(len(XX))


y_true, y_pred = y, XX
# 计算 RMSE
rmse = np.sqrt(mean_squared_error(y_true, y_pred))

# 计算 R2
r2 = r2_score(y_true, y_pred)

# 计算 Bias
bias = np.mean(y_pred - y_true)

# 计算 ubRMSE
slope, intercept, _, _, _ = linregress(y_pred, y_true)
ubrmse = np.sqrt(np.mean((y_true - (intercept + slope * y_pred))**2))

pdep, confi = gam.partial_dependence(term=0, X=XX, width=0.95)
axs.plot(XX[:], pdep, color='blue', label='Partial Dependence')
axs.fill_between(XX[:], confi[:, 0], confi[:, 1], color='blue', alpha=0.3)
axs.scatter(X, y, color='black', alpha=0.5, label='Data')
axs.set_xlabel('X', fontsize=12)
axs.set_ylabel('y', fontsize=12)
axs.set_title('Correlation Plot - GAM', fontsize=14)
axs.legend()

# 将指标写入图形
textstr = f'RMSE = {rmse:.4f}\nR2 = {r2:.4f}\nBias = {bias:.4f}\nubRMSE = {ubrmse:.4f}'
props = dict(boxstyle='round', facecolor='white', alpha=0.5)
# 'top', 'bottom', 'center', 'baseline', 'center_baseline'
axs.text(0.05, 0.95, textstr, transform=axs.transAxes, fontsize=12,
         verticalalignment='center_baseline', bbox=props)

plt.tight_layout()
plt.show()

声明：
本人作为一名作者，非常重视自己的作品和知识产权。在此声明，本人的所有原创文章均受版权法保护，未经本人授权，任何人不得擅自公开发布。
本人的文章已经在一些知名平台进行了付费发布，希望各位读者能够尊重知识产权，不要进行侵权行为。任何未经本人授权而将付费文章免费或者付费（包含商用）发布在互联网上的行为，都将视为侵犯本人的版权，本人保留追究法律责任的权利。
谢谢各位读者对本人文章的关注和支持！