【力扣周赛】第347场周赛

- 6457. 移除字符串中的尾随零
- - 题目描述
  - 解题思路
- 2711. 对角线上不同值的数量差
- - 题目描述
  - 解题思路
- 6455. 使所有字符相等的最小成本
- - 题目描述
  - 解题思路
- 6456. 矩阵中严格递增的单元格数
- - 题目描述
  - 解题思路

6457. 移除字符串中的尾随零

题目描述

描述：给你一个用字符串表示的正整数 num ，请你以字符串形式返回不含尾随零的整数 num 。

示例 1：

输入：num = "51230100"
输出："512301"
解释：整数 "51230100" 有 2 个尾随零，移除并返回整数 "512301" 。

示例 2：

输入：num = "123"
输出："123"
解释：整数 "123" 不含尾随零，返回整数 "123" 。

提示：

1 <= num.length <= 1000
num 仅由数字 0 到 9 组成
num 不含前导零

解题思路

难度：简单。

思路：最直观的想法是，从后向前遍历字符串，如果当前为0，则将其从字符串删除。

class Solution {
public:
    string removeTrailingZeros(string num) {
        int n=num.size();
        int i=n-1;
        while(i>=0&&num[i]=='0') 
        {
            num.pop_back();
            i--;
        }
        return num;
    }
};

2711. 对角线上不同值的数量差

题目描述

描述：给你一个下标从 0 开始、大小为 m x n 的二维矩阵 grid ，请你求解大小同样为 m x n 的答案矩阵 answer 。

矩阵 answer 中每个单元格 (r, c) 的值可以按下述方式进行计算：

令 topLeft[r][c] 为矩阵 grid 中单元格 (r, c) 左上角对角线上不同值的数量。
令 bottomRight[r][c] 为矩阵 grid 中单元格 (r, c) 右下角对角线上不同值的数量。
然后 answer[r][c] = |topLeft[r][c] - bottomRight[r][c]| 。

返回矩阵 answer 。

矩阵对角线是从最顶行或最左列的某个单元格开始，向右下方向走到矩阵末尾的对角线。

如果单元格 (r1, c1) 和单元格 (r, c) 属于同一条对角线且 r1 < r ，则单元格 (r1, c1) 属于单元格 (r, c) 的左上对角线。类似地，可以定义右下对角线。

示例 1：

在这里插入图片描述

输入：grid = [[1,2,3],[3,1,5],[3,2,1]]
输出：[[1,1,0],[1,0,1],[0,1,1]]
解释：第 1 个图表示最初的矩阵 grid 。 
第 2 个图表示对单元格 (0,0) 计算，其中蓝色单元格是位于右下对角线的单元格。
第 3 个图表示对单元格 (1,2) 计算，其中红色单元格是位于左上对角线的单元格。
第 4 个图表示对单元格 (1,1) 计算，其中蓝色单元格是位于右下对角线的单元格，红色单元格是位于左上对角线的单元格。
- 单元格 (0,0) 的右下对角线包含 [1,1] ，而左上对角线包含 [] 。对应答案是 |1 - 0| = 1 。
- 单元格 (1,2) 的右下对角线包含 [] ，而左上对角线包含 [2] 。对应答案是 |0 - 1| = 1 。
- 单元格 (1,1) 的右下对角线包含 [1] ，而左上对角线包含 [1] 。对应答案是 |1 - 1| = 0 。
其他单元格的对应答案也可以按照这样的流程进行计算。

示例 2：

输入：grid = [[1]]
输出：[[0]]
解释：- 单元格 (0,0) 的右下对角线包含 [] ，左上对角线包含 [] 。对应答案是 |0 - 0| = 0 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n, grid[i][j] <= 50

解题思路

难度：中等。

思路：最直观的想法是，遍历二维矩阵，使用(i,j)表示当前元素坐标，对于每一个元素，使用set集合topleft存储该元素左上角不同值，分别使用(i–,j–)表示当前元素左上角元素坐标，使用set集合bottomright存储该元素右下角不同值，分别使用(i++,j++)表示当前元素右下角元素坐标。

#include<stdlib.h>
class Solution {
public:
    vector<vector<int>> differenceOfDistinctValues(vector<vector<int>>& grid) {
        int m=grid.size();
        int n=grid[0].size();
        vector<vector<int>> res;
        for(int i=0;i<m;i++)
        {
            vector<int> temp;
            for(int j=0;j<n;j++)
            {
                unordered_set<int> topleft;  //左上角不同值
                unordered_set<int> bottomright;  //右下角不同值
                int row=i-1;
                int col=j-1;
                //左上角
                while(row>=0&&col>=0)
                {
                    topleft.insert(grid[row][col]);
                    row--;
                    col--;
                }
                //右下角
                int a=i+1;
                int b=j+1;
                while(a<m&&b<n)
                {
                    bottomright.insert(grid[a][b]);
                    a++;
                    b++;
                }
                int ans=topleft.size()>bottomright.size()?topleft.size()-bottomright.size():bottomright.size()-topleft.size();
                temp.push_back(ans);
            }
            res.push_back(temp);
        }
        return res;
    }
};

6455. 使所有字符相等的最小成本

题目描述

描述：给你一个下标从 0 开始、长度为 n 的二进制字符串 s ，你可以对其执行两种操作：

选中一个下标 i 并且反转从下标 0 到下标 i（包括下标 0 和下标 i ）的所有字符，成本为 i + 1 。
选中一个下标 i 并且反转从下标 i 到下标 n - 1（包括下标 i 和下标 n - 1 ）的所有字符，成本为 n - i 。
返回使字符串内所有字符相等需要的最小成本。

反转字符意味着：如果原来的值是 ‘0’ ，则反转后值变为 ‘1’ ，反之亦然。

示例 1：

输入：s = "0011"
输出：2
解释：执行第二种操作，选中下标 i = 2 ，可以得到 s = "0000" ，成本为 2 。可以证明 2 是使所有字符相等的最小成本。

示例 2：

输入：s = "010101"
输出：9
解释：执行第一种操作，选中下标 i = 2 ，可以得到 s = "101101" ，成本为 3 。
执行第一种操作，选中下标 i = 1 ，可以得到 s = "011101" ，成本为 2 。
执行第一种操作，选中下标 i = 0 ，可以得到 s = "111101" ，成本为 1 。
执行第二种操作，选中下标 i = 4 ，可以得到 s = "111110" ，成本为 2 。
执行第一种操作，选中下标 i = 5 ，可以得到 s = "111111" ，成本为 1 。
使所有字符相等的总成本等于 9 。可以证明 9 是使所有字符相等的最小成本。

提示：

1 <= s.length == n <= 105
s[i] 为 ‘0’ 或 ‘1’

解题思路

使所有字符相等的最小成本：最直观的想法是，从头到尾遍历字符串，如果当前字符和前一个字符不相等则需要翻转，翻转时选择子字符串[0,i-1]或者[i,n-1]两者中成本最小的，这样可以保证[0,i]部分字符全部相等，[i,n-1]部分翻转后仍不相等，故仍然需要从前向后遍历。

long long minimumCost(string s) 
{
    long long ans=0;
    int n=s.length();
    for(int i=1;i<n;i++)
    {
       if(s[i-1]!=s[i])
       	 //翻转[0,i-1]或者[i,n-1]
         ans+=min(i,n-i);
    }
    return ans;
}

总结：妙啊！题目示例具有迷惑性！

6456. 矩阵中严格递增的单元格数

题目描述

描述：给你一个下标从 1 开始、大小为 m x n 的整数矩阵 mat，你可以选择任一单元格作为起始单元格。

从起始单元格出发，你可以移动到同一行或同一列中的任何其他单元格，但前提是目标单元格的值严格大于当前单元格的值。

你可以多次重复这一过程，从一个单元格移动到另一个单元格，直到无法再进行任何移动。

请你找出从某个单元开始访问矩阵所能访问的单元格的最大数量。

返回一个表示可访问单元格最大数量的整数。

示例 1：

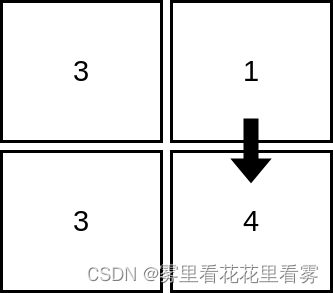
在这里插入图片描述

输入：mat = [[3,1],[3,4]]
输出：2
解释：上图展示了从第 1 行、第 2 列的单元格开始，可以访问 2 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 2 个单元格，因此答案是 2 。

示例 2：

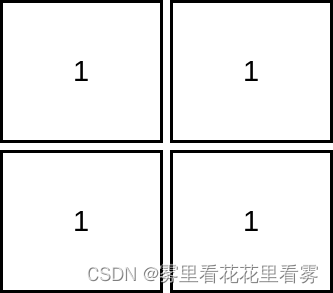
在这里插入图片描述

输入：mat = [[1,1],[1,1]]
输出：1
解释：由于目标单元格必须严格大于当前单元格，在本示例中只能访问 1 个单元格。

示例 3：

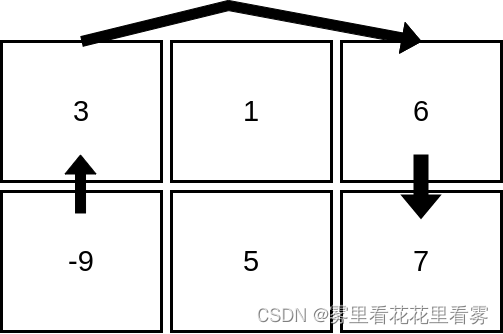
在这里插入图片描述

输入：mat = [[3,1,6],[-9,5,7]]
输出：4
解释：上图展示了从第 2 行、第 1 列的单元格开始，可以访问 4 个单元格。可以证明，无论从哪个单元格开始，最多只能访问 4 个单元格，因此答案是 4 。

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 105
1 <= m * n <= 105
-105 <= mat[i][j] <= 105

解题思路

难度：难。

思路：最直观的想法是，由于目标单元格严格大于当前单元格，即数值从小往大转移，那么可以使用一个map存储(值，坐标集合)，这样得到的集合即为按照数值从小到大排序的集合，其中值相同的为一组。假设dp[i][j]表示到达坐标(i,j)所经过的最大单元格数，那么递推公式为dp[i][j]=max(row_max[i],col_max[j])+1，其中row_max[i]表示第i行最大f值，col_max[j]表示第j列最大f值。遍历map，首先计算同组的dp值，然后更新同组的最大f值，即可。

int maxIncreasingCells(vector<vector<int>>& mat) 
{
   int m=mat.size();
   int n=mat[0].size();
   // 存储结果
   int res=0; 
   // 存储每一行最大f值以及每一列最大f值
   vector<int> row_max(m),col_max(n);
   // <value,[{i1,j1},{i2,j2}...]> 注意 相同值存储在同一组
   map<int,vector<pair<int,int>>> vmap;
   // 注意 相同值存储在同一组
   for(int i=0;i<m;i++)
   {
        for(int j=0;j<n;j++)
        {
           vmap[mat[i][j]].push_back({i,j});
        }
   }
   // map本身有序 故会按照元素值从小到大计算 其中同组的会先计算再更新 比如 3 1 3 4 第一列的两个3计算
   for(auto& [value,pos]:vmap) //&表示可以被改变 []表示接受复杂类型
   {
        vector<int> mx;
        //计算同组的最大f值
        for(auto& [i,j]:pos)
        {
           //dp公式 max(row_max[i],col_max[j])+1 计算当前行与当前列中最大f值 +1表示算当前单元格
           mx.push_back(max(row_max[i],col_max[j])+1);
           res=max(res,mx.back());
        }
        //更新同组的最大f值
        for(int k=0;k<pos.size();k++)
        {
           auto &[i,j]=pos[k];
           row_max[i]=max(row_max[i],mx[k]);
           col_max[j]=max(col_max[j],mx[k]);
           // cout<<"i="<<i<<";j="<<j<<"value="<<value<<";mx["<<k<<"]="<<mx[k]<<";row_max["<<i<<"]="<<row_max[i]<<";col_max["<<j<<"]="<<col_max[j]<<endl;
        }
    }
    return res;
}

错误：一开始，我拿到这个题，感觉比“使所有字符相等的最小成本”那题好想一些，于是琢磨，应该选择从矩阵中最小数值开始出发，然后选择该值所在行或者所在列中尚未访问过的且比该值大的最小值，依次类推，直至不能再移动为止，但是我发现，测试案例[[-1,5,-9],[-2,-5,0]]无法通过，后来一想，那么将选择从矩阵中最小数值开始出发转为从矩阵中任意数值出发，然后统计所有数值出发的所达数量最大值即可，后来发现，测试案例[[3,-8],[8,1],[2,-5]]无法通过，即最后只通过168个测试案例，我就觉得应该是解题思路错误了，不过第一次尝试困难题，第一次能坚持想法写下来，第一次能通过困难题1/3测试案例，我觉得很棒了哈哈哈哈，继续加油啦！

// 一开始的错误写法1 留作纪念
class Solution {
public:
    //寻找最小值所在行或者所在列的相对最小值较大的值
    vector<int> dfs(int& res,vector<vector<int>>& mat,vector<vector<bool>>& visit,int m,int n,int row,int col,int val)
    {
        int minrow=-1;
        int mincol=-1;
        int minval=val;
        map<int,vector<int>> num;
        //行
        for(int i=0;i<n;i++)
        {
            if(!visit[row][i]&&i!=col&&mat[row][i]>val)
            {
                num[mat[row][i]]={row,i};
            }
        }
        //列
        for(int i=0;i<m;i++)
        {
            if(!visit[i][col]&&i!=row&&mat[i][col]>val)
            {
                num[mat[i][col]]={i,col};
            }
        }
        minrow=num.size()?num.begin()->second[0]:-1;
        mincol=num.size()?num.begin()->second[1]:-1;
        minval=num.size()?num.begin()->first:-1;
        if(minrow!=-1&&mincol!=-1)
        {
            visit[minrow][mincol]=true;
            res++;
        }
        return {minrow,mincol,minval};
    }
    int maxIncreasingCells(vector<vector<int>>& mat) {
        int m=mat.size();
        int n=mat[0].size();
        vector<vector<bool>> visit(m,vector<bool>(n,false));
        int res=1; //基础为1
        int minrow=-1;
        int mincol=-1;
        int minval=INT_MAX;
        //寻找最小点作为出发值
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                if(mat[i][j]<minval)
                {
                    minval=mat[i][j];
                    minrow=i;
                    mincol=j;
                }
            }
        }
        //置访问标志
        visit[minrow][mincol]=true;
        while(minrow!=-1&&mincol!=-1)
        {
            vector<int> temp;
            temp = dfs(res,mat,visit,m,n,minrow,mincol,minval);
            for(auto n:temp)
                cout<<n<<endl;
            minrow = temp[0];
            mincol = temp[1];
            minval = temp[2];
        }
        return res;
    }
};

// 一开始的错误写法2 留作纪念
class Solution {
public:
    //寻找最小值所在行或者所在列的相对最小值较大的值
    vector<int> dfs(int& res,vector<vector<int>>& mat,vector<vector<bool>>& visit,int m,int n,int row,int col,int val)
    {
        int minrow=-1;
        int mincol=-1;
        int minval=val;
        map<int,vector<int>> num;
        //行
        for(int i=0;i<n;i++)
        {
            if(!visit[row][i]&&i!=col&&mat[row][i]>val)
            {
                num[mat[row][i]]={row,i};
            }
        }
        //列
        for(int i=0;i<m;i++)
        {
            if(!visit[i][col]&&i!=row&&mat[i][col]>val)
            {
                num[mat[i][col]]={i,col};
            }
        }
        minrow=num.size()?num.begin()->second[0]:-1;
        mincol=num.size()?num.begin()->second[1]:-1;
        minval=num.size()?num.begin()->first:-1;
        if(minrow!=-1&&mincol!=-1)
        {
            visit[minrow][mincol]=true;
            res++;
        }
        return {minrow,mincol,minval};
    }
    int maxIncreasingCells(vector<vector<int>>& mat) {
        int m=mat.size();
        int n=mat[0].size();
        int res=1; //基础为1
        //寻找最小点作为出发值
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                int minrow=i;
                int mincol=j;
                int minval=mat[i][j];
                int ans=1;
                vector<vector<bool>> visit(m,vector<bool>(n,false));
                //置访问标志
                visit[minrow][mincol]=true;
                while(minrow!=-1&&mincol!=-1)
                {
                    vector<int> temp;
                    temp = dfs(ans,mat,visit,m,n,minrow,mincol,minval);
                    minrow = temp[0];
                    mincol = temp[1];
                    minval = temp[2];
                }
                res=max(res,ans);
            }
        }
        return res;
    }
};

总结：有点难，但还好，继续加油！