数的概念与结构

线性表：是一种具有n个相同特性的数据元素的有限序列。线性表逻辑上是线性结构，也就是连成的一条直线，但一条直线上的数据元素并不是一定要物理结构连续的。

讲到二叉树之前，我们要先了解一下什么是树，首先树也是一种数据结构，只不过与栈和队列不同，树并不是线性表的一种，因为树的结构组成并不是直线型的，是有分支的。

 树的概念

树是一种非线性的数据结构，由n（n>=0）有限的节点构成的具有层次关系的结构。而结构十分像一棵倒着的树，节点A就像树根一样（根节点）没有前驱节点，而A下面就类似于一个个树枝（子树）一样，而树枝又会分支，分支又有分支...是否会联想到递归了你。

 注意：树的结构中，子树是不存在交集的（除了根节点，每个节点有且只有一个父节点），否则就不是树的结构

 而以上的三种结构就都不是树结构。

树中的常见名词 

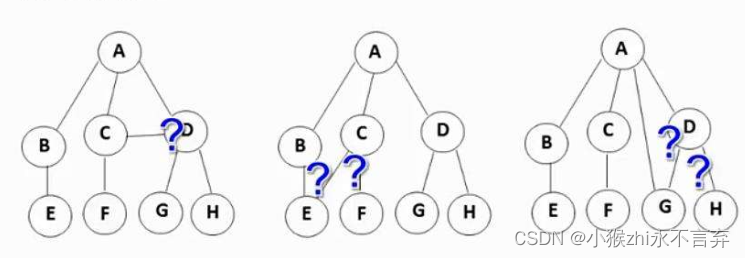
有关树的名词可以联想到家里的亲戚关系 

 节点的度：一个节点含有的子树（分支）的个数称为该节点的度； 如上图：A的度为6
叶节点或终端节点：就像是树叶一样（不再分支），即度为0的节点称为叶节点； 如上图：B、C、H、I 等节点为叶节点（终端节点）
非终端节点或分支节点：与上面相反，有分支的节点，即度不为0的节点； 如上图：D、E、F、G 等节点为分支节点
双亲节点或父节点：若一个树含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点
孩子节点或子节点：与上面相反，一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点
（亲）兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点
树的度：一棵树中，最大的 节点的度 称为树的度； 如上图：树的度为6
节点的层次：从根开始定义起，根为第1层，根的（所有）子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次； 如上图：树的高度为4
堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先，E也是Q的祖先
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙

森林：多棵互不相交的树的集合称为森林（并查集）

树的结构表示 

树的表示方式就不会像单链表一样简单，树中要存放数据，和节点之间的关系，而节点之间的关系并不像单链表一样，因为树并不是线性结构，树的分支并不是一定只有一个，可能没有，也可能有多个，那么我们要创建多个指针吗，如果不知道树的高度呢，就算知道了会不会太复杂呢。所以我们一般会有更加简便的定义方式：孩子兄弟表示法。即创建树的节点存放实际数据，孩子指针，兄弟指针。

typedef int DataType;
struct Node
{
    DataType data; // 结点中的数据域
    struct Node* firstChild1; // 第一个孩子结点
    struct Node* pNextBrother; // 指向其下一个兄弟结点
};

 这样是不是就将每一个节点都串联起来了呢，没有的时候就指向空。

二叉树的概念与结构

概念

1. 二叉树中每个节点的度都小于等于2。

2. 二叉树的子树分左右，次序不能颠倒，所以二叉树称为有序数。

特殊二叉树

满二叉树：二叉树每个节点的度都达到最大值（2），由此可有等比求和计算出节点总数：2^k-1

完全二叉树：除了最后一层。前面节点的度都满了，最后一层可以不满，但是必须从左至右连续，所以满二叉树也是完全二叉树的一种特殊形式，其总结点的范围在：2^(k-1) ~ 2^k-1

二叉树的存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。

顺序存储

顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树的话会有空间的浪费。而一般只有堆才会使用数组来存储，二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

链式存储

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的结点的存储地址 。

二叉树的顺序结构与实现

 二叉树的顺序结构

完全二叉树的形式可以很好的与数组契合，因为节点的连续性，所以用顺序表结构的数组存储完全二叉树是十分合适的，并且可以直接通过数组下标的关系找到对应的子节点和父节点。

 而对于二叉树的其他形式是不适合用数组来存储的，可能会复杂并且存在空间的浪费。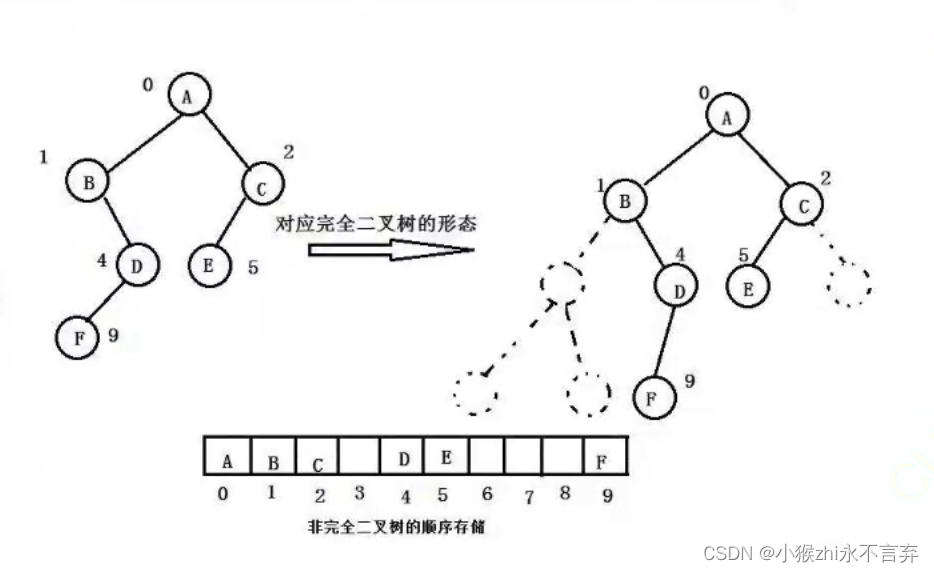

堆的概念与结构 

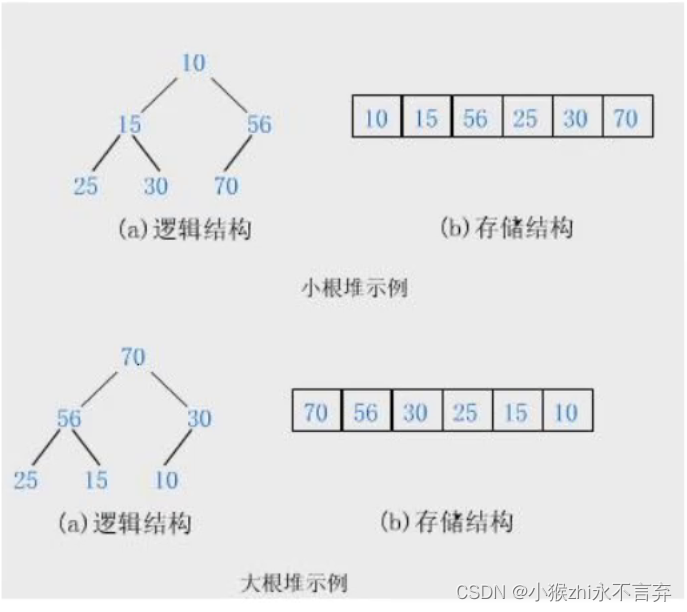
首先我们要知道，堆的结构是完全二叉树，并且推也分为两种：大（根）堆，小（根）堆。

 而堆也只有大堆和小堆两种形式，其他不满足条件的都不属于堆。

大（根）堆：树中的任意一个节点存储的值都小于等于其父节点存储的的值

小（根 ）堆：树中的任意一个节点存储的值都大于等于其父节点存储的的值

堆的基本实现

 堆是可以用顺序表结构的数组来实现的，所以可以借鉴前面栈的实现方法，而下面介绍的是大（根）堆的写法：

需要实现的函数

typedef struct Heap
{
	int sz;
	int capacity;
	int* arr;

}Heap;

void Init(Heap* hp);//初始化堆
void Push(Heap* hp, int x);//增数据
void Pop(Heap* hp);//删数据
int GetTop(Heap* hp);//得到根数据
void Destroy(Heap* hp);//空间释放

void Init(Heap* hp)
{
	hp->arr = (int*)malloc(sizeof(int) * 3);
	hp->capacity = 3;
	hp->sz = 0;//指向实际数据的下一个节点
}

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 =  *p2;
	*p2 = tmp;
}

void Adjust_up(int* arr,int child)
{
	while (child > 0)
	{
		int parent = (child - 1) / 2;//不可以作为while的条件，child==0时
		if (arr[child] > arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			child = parent;
		}
		else
			return;

	}
}
void Push(Heap* hp, int x)
{
	if (hp->sz == hp->capacity)
	{
		hp->capacity *= 2;
		int* tmp = (int*)realloc(hp->arr, sizeof(int) * hp->capacity);
		assert(tmp);
		hp->arr = tmp;
	}
	hp->arr[hp->sz] = x;
	
	hp->sz++;
	//向上调整保证是堆
	Adjust_up(hp->arr,hp->sz-1);
}

void Adjust_down(int* arr,int last)
{
	int parent = 0;
	int child = parent * 2 + 1;//假设较大值是左孩子
	while (child<last)
	{
		if (child + 1 < last && arr[child] < arr[child + 1])//先防止越界，再验证较大值（只有一个左孩子时可能会越界）
			child += 1;

		if (arr[child] > arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			return;
	}
}
void Pop(Heap* hp)//删除根节点的数据
{
	assert(hp->sz);//保证有数据
	//防止改变堆的父子大小关系，保证其他数据的关系不变，则选择尾元素换到头
	hp->arr[0] = hp->arr[hp->sz - 1];
	hp->sz--;

	//向下调整
	Adjust_down(hp->arr,hp->sz);
}

int GetTop(Heap* hp)
{
	assert(hp->sz);
	return hp->arr[0];
}

void Destroy(Heap* hp)
{
	free(hp->arr);
	 
	hp->capacity = hp->sz = 0;
}

这里其实看一下Adjust_down 和 Adjust_up 这两个函数的实现就行了，主要就是插入数据时要用到向上调整数据，而删除根元素时会用到向下调整数据，这两个函数使用之前都要保证原数据的父子关系不会发生改变，即：除了增加或删除的数据，其余子树都是堆的形式。

用堆进行排序 

经过堆的实现，我们知道一个数据按照堆去存放，根节点的值要么是最大值要么就是最小值，所以我们多进行几次不就可以依次得到最大值（最小值）。假如用实现大（根）堆的方式来实现，首先将数组中的数一个个按照向上调整建堆的方式插入进去，这样根就是最大的一个数，此时接下来就有两种途径：1.将剩余的的数继续按照向上调整的方式再次建堆，找第二大的数（这样就改变了其他数之间的父子关系，故要全部重新插入）。2.将最后一个数和根（最大值）进行交换，再运用向下调整（类似于Pop 函数）实现接下来操作（这样不会改变原数据的父子关系，所以子树依旧是大堆的形式）。所以第二种方式就轻松了很多。

---

向上调整建堆法

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void Push(int* arr,int child)
{
	while (child > 0)
	{
		int parent = (child - 1) / 2;
		if (arr[child] > arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			child = parent;
		}
		else
			return;

	}
}
void Pop(int* arr,int len)
{

	int parent = 0;
	int child = parent * 2 + 1;//假设较大值是左孩子
	while (child<len)
	{
		if (child + 1 < len && arr[child] < arr[child + 1])//先防止越界，再验证较大值（只有一个左孩子）
			child += 1;//可能存在越界

		if (arr[child] > arr[parent])
		{
			Swap(&arr[child], &arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			return;
	}
}
int main()
{

	int arr[] = { 6,1,7,0,3,5,8,2,9,4 };
	int len = sizeof(arr) / sizeof(int);
	for (int i = 1; i < len; i++)//向上建堆
	{
		Push(arr, i);//传下标
	}

	while(len>0)
	{
		Swap(&arr[0], &arr[len-1]);//将最大值放到最后面
		Pop(arr, len - 1);//传最后一个数的下一个下标
		printf("%d ", arr[len-1]);
		len--;//每循环一次就排好了一个数
	}

	return 0;
}

有一点要注意的是，每次找到最大的数换到数组的最后，则每向下调整一次就得到当前推中的最大值，数据就会逐渐少一，所以依次进行之后数据就按照升序的方式排列了，即：运用大根堆法实现升序，运用小根堆法实现降序。

向下调整建堆法

上面的堆排序其实是用到了向下调整建堆，向下调整找重建堆找最值。那么可不可以建堆也用向下调整的方式来完成呢，而在一份完整的数据面前我们想用向下调整的条件是：该节点的左右子树都是大堆（小堆）的形式才可以。

假如我们想要建立一个小堆。就以上面代码中的数组为例，我们现在的目的就是找可以向下调整的节点，即：该节点的左右子树都是小堆，而我们从图中可以确定的小堆就是最靠近叶节点的分支节点，因为该分支节点的两个分支是叶节点，故一定是小堆，即图中为3的节点，所以我们就从该位置开始向下调整，并且要逆着继续执行，找前面的分支节点，就依次从后向前，这样就可以保证你任何时候向下调整的节点的左右子树一定是堆。

步骤即：

代码实现

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void Adjust_down(int* arr, int i,int len)
{
	int parent = i;
	int child = i * 2 + 1;

	while (child < len)
	{
		if (child + 1 < len && arr[child] > arr[child + 1])//防止有右孩子不存在的情况
			child++;//找较小的子节点
		if (arr[parent] > arr[child])//如果父节点本来就小，不用换
		{
			Swap(&arr[parent], &arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			return;
	}

}
int main()
{
	int arr[]= { 6,1,7,0,3,5,8,2,9,4 };
	int len = sizeof(arr) / sizeof(int);
	//先向下调整建堆
	for (int i = (len - 1 - 1) / 2; i >= 0; i--)//i指向元素下标而len-1是最后一个元素下标
	{
		Adjust_down(arr, i,len);//len是最后一个元素的下一个下标
	}
	//向下调整找最值
	while (len > 0)
	{
		Swap(&arr[0], &arr[len - 1]);//交换一次就保留一个最小值放到最后面
		Adjust_down(arr, 0, len - 1);//此时最后一个元素就不计算在内
		printf("%d ", arr[len - 1]);//从后向前打印数据
		len--;
	}

	return 0;
}

复杂度分析

向上调整建堆：当层数节点多时，需要调整次数也多。所以数据越多，所执行调整的次数也就越多，时间复杂度也就越高。 

---

向下调整建堆：而相对于向上调整而言，向下调整建堆就明显避开了层数节点多时，需要调整次数也多等问题，恰恰相反，层数节点越多，需要调整的次数越少，时间复杂度是O(n-logn) 即：O(n) 。计算就留给你们了，和上面的方法一样。

---

而上面的方法实现堆排序的时间复杂度是O(n+n*logn)，即：O(n log n)        

堆中的TOP-K问题

我们了解到堆排序相比冒泡排序而言，效率要高得多，而且向下调整建堆又比向上调整建堆效率高，所以我们就引申到堆中的 TOP-K 的问题，即：找所有数中最大（最小）的前 K 个数。

那么直接将这给的所有数据建成堆并向下调整排序不就成了，可是1.如果给的数据过大，空间不够用呢 2.只想要前 K 个最值，这样是不是复杂了？

假如说我们要找所有数据的前5个最大的值：所以我们就想到了建一个只能存放5个数的小堆，然后依次将后面的数与堆顶的值进行比较，如果大于堆顶的数就交换，进行向下调整，重新建堆，然后依次将后面的数进行上面操作就可以完成。

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
void Adjust_down(int* arr, int i, int len)//i是下标，len是堆大小
{
	int parent = i;
	int child = parent * 2 + 1;
	while (child<len)
	{
		if (child + 1 < len && arr[child] > arr[child + 1])
			child += 1;
		if (arr[parent] > arr[child])
		{
			Swap(&arr[parent], &arr[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			return;
	}
}
int main()
{
	srand((unsigned int)time(NULL));
	FILE* pf = fopen("data.txt", "w");
	if (pf == NULL)
	{
		perror("pf=NULL");
		return 1;
	}
	for (int i = 0; i < 1000; i++)
	{
		int x = rand() % 1000;//产生一万个随机数放在文件里
		fprintf(pf, "%d\n", x);
	}
	fclose(pf);//处理完数据之后一定要及时关闭，否则数据可能丢失

	//直接开辟相应大小的空间
	int k = 7;
	int* arr  = (int*)malloc(sizeof(int) * k);
	assert(arr);
	//读取文件中前面7个数据放到数组中
	FILE* po = fopen("data.txt", "r");
	assert(po);
	
	for(int i=0;i<k;i++)
	{
		fscanf(po, "%d", &arr[i]);//将前7个数存到数组里
	}
	for (int i = (k - 2) / 2; i >= 0; i--)//七个数向下调整建小堆
	{
		Adjust_down(arr, i, k);
	}
	//读取文件后面的数据
	int val = 0;
	while (feof(po)==0)
	{
		fscanf(po, "%d", &val);
		if (val > arr[0])
		{
			arr[0] = val;
			Adjust_down(arr, 0, k);//每执行一次，堆顶都是最小值
		}
	}
	for (int i = 0; i < k; i++)
		printf("%d ", arr[i]);

	return 0;
}

而当数据过多时，我们就会把数据存在文件当中，从文件中逐一的读取数据。使用小堆其实就保证了最小值在堆顶的位置，所以我们每次新来一个值就和堆顶（最小值比较），大的话就可以直接换掉最小值，再次调整，现在堆中的最小值又在堆顶....这样就方便了很多。

---

 二叉树的链式结构的实现

前面谈到的是完全二叉树，因为结构特殊，所以我们是通过顺序表的方式存储的，但是对于一般的二叉树是并不适合的，那样会存在空间的大大浪费，并且也不方便。所以我们还是回归自然，用链表来存储二叉树。

typedef struct TreeNode
{
	int val;
	struct TreeNode* left;
	struct TreeNode* right;

}TN;

每一个节点基本的结构就是存放的数据加左右两个子节点，但是二叉树的左右子节点又可以看作是新的二叉树，这样是不是很像递归在自己调用自己呢。

 

二叉树前序中序后序遍历

我们知道完全二叉树是用顺序表来存储的，所以我们遍历顺序表，用下标就可以十分轻松的实现打印二叉树，可是链表又该如何打印数据呢？这里我们就有几种递归实现的方式。

1. 前序遍历(也称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。即：根 左 右
2. 中序遍历——访问根结点的操作发生在遍历其左右子树之中（间）。即：左 根 右
3. 后序遍历——访问根结点的操作发生在遍历其左右子树之后。即：左 右 根

这里的左节点与右节点并不一定是单纯的左右节点，他可能也看作是左子树、右子树。所以我们在不知道二叉树的图形结构式，遍历二叉树就要用到上面的方法。 

二叉树前序遍历

假设我们实现上面结构的二叉树并且想要打印出来：

 

typedef struct TreeNode//创建节点类型
{
	int val;
	struct TreeNode* left;
	struct TreeNode* right;

}TN;
TN* Malloc(int x)//动态开辟节点并初始化
{
	TN* new = (TN*)malloc(sizeof(TN));
	assert(new);
	new->left = new->right = NULL;
	new->val = x;

	return new;
}
void Print(TN* node)//前序遍历
{
	if (node == NULL)
		printf("N ");
	else
	{
		printf("%d ", node->val);
		Print(node->left);
		Print(node->right);
	}
}
int main()
{
	TN* node1 = Malloc(1);
	TN* node2 = Malloc(2);
	TN* node3 = Malloc(3);
	TN* node4 = Malloc(4);
	TN* node5 = Malloc(5);
	TN* node6 = Malloc(6);

	node1->right = node4;
	node1->left = node2;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	Print(node1);//前序打印（根左右）

	return 0;
}

递归部分分析图：

 

二叉树的中序后序遍历

其实二叉树的的中序和后序遍历就是将打印顺序改变一下就行了：

void Print(TN* node)//中序遍历
{
	if (node == NULL)
		printf("N ");
	else
	{
        Print(node->left);
		printf("%d ", node->val);
		Print(node->right);
	}
}

void Print(TN* node)//后序遍历
{
	if (node == NULL)
		printf("N ");
	else
	{
        Print(node->left);
        Print(node->right);
		printf("%d ", node->val);
	
	}
}

 

这里同样是用到递归，而且链式二叉树考的几乎都是递归实现的方式，所以我们就要了解一下递归，递归其实是和函数放到一起的，但是函数就实现一次，而递归是实现多次相同功能的函数，而且想要实现递归的精髓就两点

• 找到递归执行的停止条件（即找到向下创建函数栈帧的最后一次）
• 将问题转换成子问题（即找到等价问题进行转换）

求二叉树节点个数

int GetNodeSize(TN* node)//求节点的个数
{
	if (node==NULL)//结束条件，而且一般二叉树问题都要考虑执行到NULL的情况
		return 0;
	else
		return GetNodeSize(node->left) + GetNodeSize(node->right) + 1;
        //左子树的节点个数+右子树的节点个数+自生的一个节点
}

求二叉树的叶子结点个数

int GetLeafSize(TN* node)//求叶子结点的个数
{
	if (node == NULL)//终止条件
		return 0;
	if (node->left == node->right && node->left == NULL)//是叶子结点
		return 1;
	else
		return GetLeafSize(node->left) + GetLeafSize(node->right);
        //等价成 左子树的叶子结点个数+右子树的叶子结点个数
}

求二叉树的高度

int GetTreeHeight(TN* node)//求二叉树的高度
{
	if (node == NULL)//终止
		return 0;
	
	//return GetTreeHeight(node->left) > GetTreeHeight(node->right) ?
	//	1 + GetTreeHeight(node->left) : 1 + GetTreeHeight(node->right);//这样实现会先判断大小再计算值，导致重复实现递归
	//上述递归调用太多，导致反复调用，成等比增长，所以就会导致花费时间更久

	int left = GetTreeHeight(node->left);//左子树的高度
	int right = GetTreeHeight(node->right);//右子树的高度
	return left > right ? left + 1 : right + 1;//返回更大的高度

}

求二叉树第K层节点个数

int GetKNode(TN* node,int k)
{
	//停止条件
	if (k == 1 && node != NULL)//因为传过来的节点就看作第一层，所以k==1就是所求
		return 1;
	if (node == NULL)
		return 0;
	return GetKNode(node->left, k - 1) + GetKNode(node->right, k - 1);
    //等价转换成 左子树的k-1层节点数+右子树的k-1层节点数
}

查找二叉树中值为x的节点

TN* GetPointNode(TN* node, int x)
{
	if (node == NULL)
		return NULL;
	if (node->val == x)//相同就直接返回节点指针
		return node;

	//if (GetPointNode(node->left, x) != NULL)
	//	return GetPointNode(node->left, x);
	//if (GetPointNode(node->right, x) != NULL)
	//	return GetPointNode(node->right, x);
	//消耗过大
    
    //以下是该节点既不是空也不是指定节点的情况，继续向下找：
	TN* leftnode = GetPointNode(node->left, x);//记录下来
	if (leftnode != NULL)//判断左子树是否存在指定节点
		return leftnode;

	TN* rightnode = GetPointNode(node->right, x);
	if (rightnode != NULL)//右子树
		return rightnode;
	return NULL;//该节点处没找到并且左右节点也不是

}

---

图文解析就不画了，交给你们自己来。