简介
在介绍卷积和相关运算之前,需要先认识一些更加基本的运算
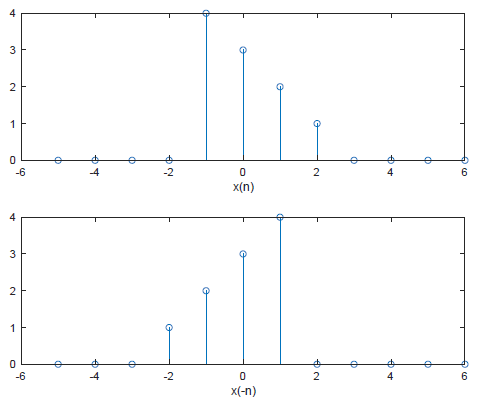
翻折
- 设某一序列x(n),则x(-n)是以n=0的纵轴为对称轴,将x(n)加以翻折得到的
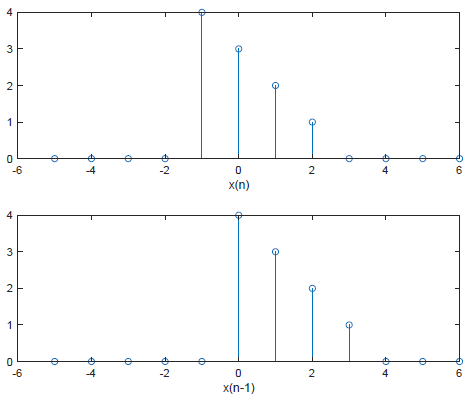
移位
- 设某一序列x(n),m为正整数,x(n-m)表示x(n)逐项依次延时(右移)m位
- 左加右减规则:即x(n-m)表示逐项依次右移,x(n+m)表示逐项依次左移
- 注意:上述说法,当且仅当变量n的系数为1时,才成立。例如:对于序列x(-n-1),需要变换成x(-(n+1)),变换顺序为
x
(
n
)
→
x
(
−
n
)
→
x
(
−
(
n
+
1
)
)
x(n) \rightarrow x(-n) \rightarrow x(-(n+1))
x(n)→x(−n)→x(−(n+1)),即先翻折,再移位
和、积、累加、差分
- 和: z ( n ) = x ( n ) + y ( n ) z(n)=x(n)+y(n) z(n)=x(n)+y(n)
- 积: z ( n ) = x ( n ) ⋅ y ( n ) z(n)=x(n) \cdot y(n) z(n)=x(n)⋅y(n)
- 累加: y ( n ) = ∑ k = − ∞ n x ( k ) y(n)=\sum_{k=-\infty}^{n} x(k) y(n)=∑k=−∞nx(k),历史数据累积求和(Cumulative Sum)
- 差分: y ( n ) = x ( n ) − x ( n − 1 ) y(n)=x(n)-x(n-1) y(n)=x(n)−x(n−1),一阶差分具有高通滤波效果
尺度变换
- 对于序列x(n),形如x(mn)或者 x ( n m ) x(\frac{n}{m}) x(mn)(m为正整数)的序列,为x(n)的尺度变换序列
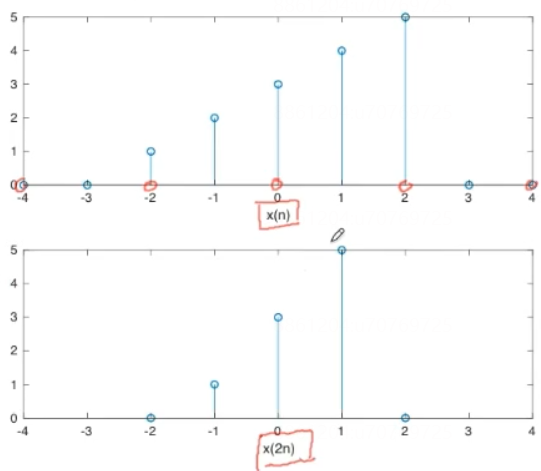
- 例如:当m=2,x(2n)是以低一倍的抽样频率从x(n)中,每隔两点取一点,这种运算也称为抽取,通常表示为
↓
2
\downarrow 2
↓2,实际运行中,通常保持0点对齐,取走奇数点,保留偶数点
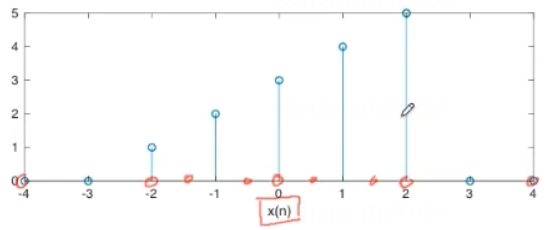
- 类似地,
x
(
n
2
)
x(\frac{n}{2})
x(2n)称为插值,先确定需要插值的位置,然后根据相邻的采样点确定值
线性卷积
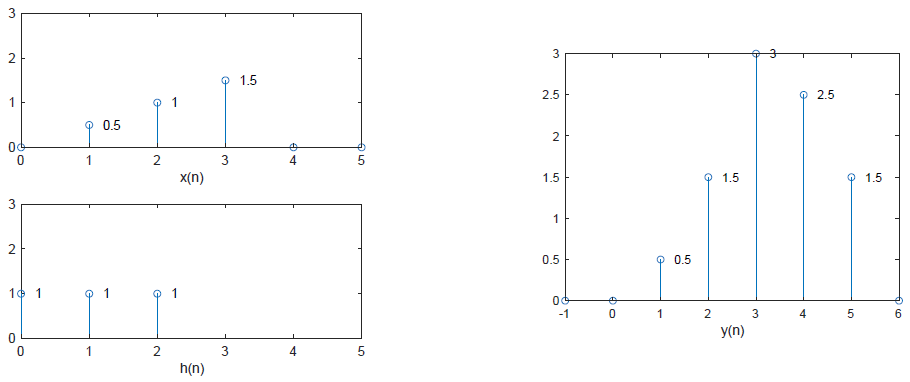
- 定义式: y ( n ) = ∑ m = − ∞ ∞ x ( m ) h ( n − m ) = x ( n ) ∗ h ( n ) y(n)=\sum_{m=-\infty}^{\infty} x(m)h(n-m)=x(n)*h(n) y(n)=∑m=−∞∞x(m)h(n−m)=x(n)∗h(n)
- 根据定义式,可知线性卷积包含四个步骤:翻折、移位、相乘(积)、累加
- 变换顺序 h ( m ) → h ( − m ) → h ( − ( m − n ) ) h(m) \rightarrow h(-m) \rightarrow h(-(m-n)) h(m)→h(−m)→h(−(m−n))
- y(n)的计算
- 当n=0, y ( 0 ) = ∑ m = − ∞ ∞ x ( m ) h ( − m ) = 0 y(0)=\sum_{m=-\infty}^{\infty} x(m)h(-m)=0 y(0)=∑m=−∞∞x(m)h(−m)=0
- 当n=1, y ( 1 ) = ∑ m = − ∞ ∞ x ( m ) h ( − ( m − 1 ) ) = 0.5 y(1)=\sum_{m=-\infty}^{\infty} x(m)h(-(m-1))=0.5 y(1)=∑m=−∞∞x(m)h(−(m−1))=0.5
- 当n=2, y ( 1 ) = ∑ m = − ∞ ∞ x ( m ) h ( − ( m − 2 ) ) = 0.5 + 1 = 1.5 y(1)=\sum_{m=-\infty}^{\infty} x(m)h(-(m-2))=0.5+1=1.5 y(1)=∑m=−∞∞x(m)h(−(m−2))=0.5+1=1.5
- …
-
卷积满足交换律,即 y ( n ) = x ( n ) ∗ h ( n ) = h ( n ) ∗ x ( n ) y(n)=x(n)*h(n)=h(n)*x(n) y(n)=x(n)∗h(n)=h(n)∗x(n)
-
设x(n)的长度为 N 1 N_1 N1,h(n)的长度为 N 2 N_2 N2,则y(n)的长度为 N 1 + N 2 − 1 N_1+N_2-1 N1+N2−1。原因:当 h ( − ( m − n ) ) h(-(m-n)) h(−(m−n))移位至,h(0)与x(4)对齐时(如下图),对应的 y ( N 1 + N 2 − 1 ) = y ( 6 ) y(N_1+N_2-1)=y(6) y(N1+N2−1)=y(6)必为0,因此包括y(6)及往后的值都是无意义的, y ( N 1 + N 2 − 2 ) y(N_1+N_2-2) y(N1+N2−2)是最后一个有意义的值,从而y(n)长度为 N 1 + N 2 − 1 N_1+N_2-1 N1+N2−1
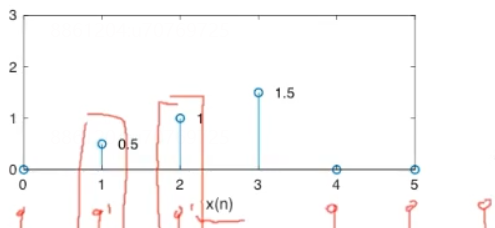
-
线性卷积的另一种理解:线性卷积实际上是一个信号在另一个信号上的加权叠加
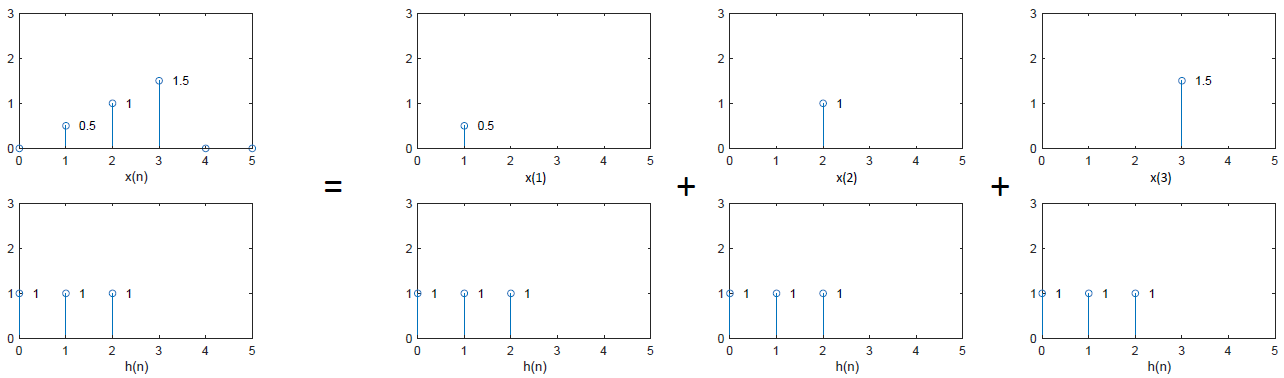
-
线性系统满足可加性和齐次性
- 可加性: x 1 ( n ) + x 2 ( n ) → y 1 ( n ) + y 2 ( n ) x_1(n)+x_2(n) \rightarrow y_1(n)+y_2(n) x1(n)+x2(n)→y1(n)+y2(n)
- 齐次性: α x ( n ) → α y ( n ) \alpha x(n) \rightarrow \alpha y(n) αx(n)→αy(n)
-
时不变系统表示: x ( n − m ) = y ( n − m ) x(n-m)=y(n-m) x(n−m)=y(n−m),即系统的输出信号,与输入信号的施加时刻,没有关系
-
对于线性时不变系统,如果已知系统的单位冲激响应h(n),那么将单位冲激响应与输入信号x(n)求线性卷积,就得到了输出信号y(n)

-
线性卷积的应用:模拟远场数据
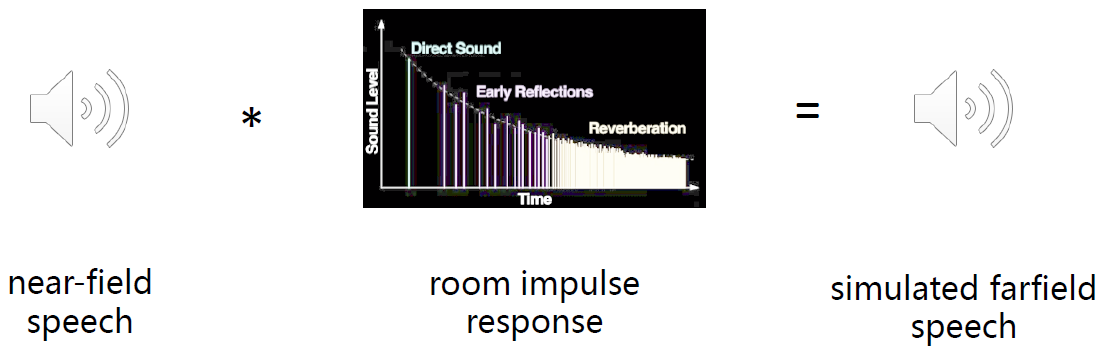
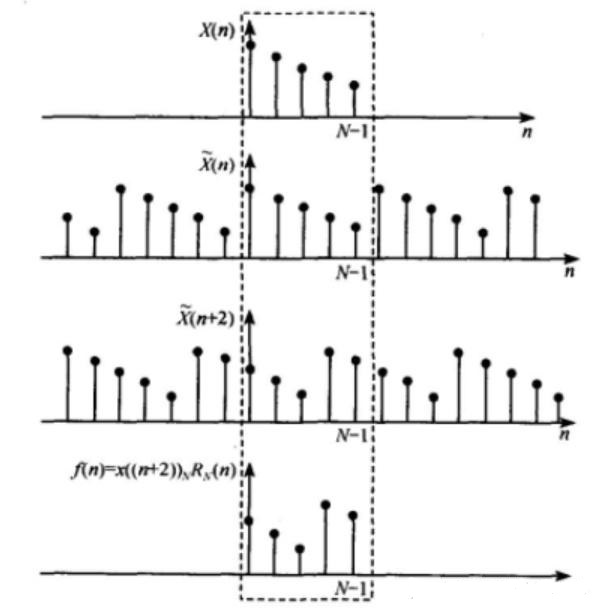
圆周移位
- 定义式: x m ( n ) = x ( ( n + m ) ) N R N ( n ) x_m(n)=x((n+m))_N R_N(n) xm(n)=x((n+m))NRN(n)
- 其中
- x ( ( n + m ) ) N x((n+m))_N x((n+m))N表示x(n)经过周期(N)延拓后的序列,再移位m
-
R
N
(
n
)
R_N(n)
RN(n)表示取主值序列
R N ( n ) = { 1 , 0 ≤ n ≤ N − 1 0 , o t h e r s R_N(n)=\left\{\begin{matrix} &1&,0 \le n \le N-1\\ &0&,others \end{matrix}\right. RN(n)={10,0≤n≤N−1,others
圆周卷积
- 如果
x
1
(
n
)
x_1(n)
x1(n)和
x
2
(
n
)
x_2(n)
x2(n)都是长度为N的有限长序列
并且: D F T [ x 1 ( n ) ] = X 1 ( k ) , D F T [ x 2 ( n ) ] = X 2 ( k ) , Y ( k ) = X 1 ( k ) X 2 ( k ) 则: y ( n ) = I D F T [ Y ( k ) ] = [ ∑ m = 0 N − 1 x 1 ( m ) x 2 ( ( n − m ) ) N ] R N ( n ) = [ ∑ m = 0 N − 1 x 2 ( m ) x 1 ( ( n − m ) ) N ] R N ( n ) 定义为 x 1 ( n ) 和 x 2 ( n ) 的圆周卷积 \begin{aligned} &并且:DFT[x_1(n)]=X_1(k),DFT[x_2(n)]=X_2(k),Y(k)=X_1(k)X_2(k) \\ &则:y(n)=IDFT[Y(k)]=[\sum_{m=0}^{N-1}x_1(m)x_2((n-m))_N]R_N(n)=[\sum_{m=0}^{N-1}x_2(m)x_1((n-m))_N]R_N(n) \\ &定义为x_1(n)和x_2(n)的圆周卷积 \end{aligned} \\ 并且:DFT[x1(n)]=X1(k),DFT[x2(n)]=X2(k),Y(k)=X1(k)X2(k)则:y(n)=IDFT[Y(k)]=[m=0∑N−1x1(m)x2((n−m))N]RN(n)=[m=0∑N−1x2(m)x1((n−m))N]RN(n)定义为x1(n)和x2(n)的圆周卷积 - 注意,与线性卷积相比,圆周卷积多了周期延拓和取主值序列两个步骤,因此必须指定圆周卷积的点数N
- 时域信号的圆周卷积等于,其对应傅里叶变换频域信号的乘积,再傅里叶逆变换为时域信号
线性卷积和圆周卷积的关系
- 给定两个有限长序列
x
1
(
n
)
,
x
2
(
n
)
x_1(n),x_2(n)
x1(n),x2(n),长度分别为
N
1
=
5
,
N
2
=
3
N_1=5,N_2=3
N1=5,N2=3,研究线性卷积和圆周卷积的点数为
N
1
N_1
N1范围内的值
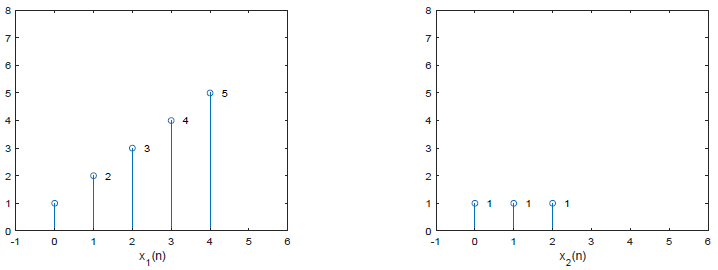
- 这两个序列的线性卷积和圆周卷积结果如下
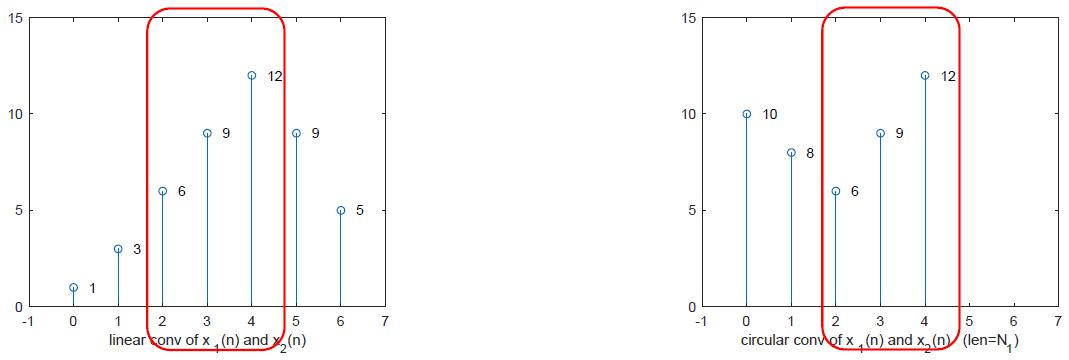
- 一般地,如果两个有限长序列的长度为 N 1 , N 2 N_1,N_2 N1,N2,且满足 N 1 ≥ N 2 N_1 \ge N_2 N1≥N2,则圆周卷积的后 N 1 − N 2 + 1 N_1-N_2+1 N1−N2+1个点,与线性卷积的结果一致。原因:当 x 2 ( n ) x_2(n) x2(n)完全移入 x 1 ( n ) x_1(n) x1(n)后,即移 N 2 − 1 N_2-1 N2−1位后,线性卷积和圆周卷积结果一致,因此剩余的 N 1 − ( N 2 − 1 ) N_1-(N_2-1) N1−(N2−1)位中,线性卷积和圆周卷积结果一致
线性相关
- 定义式: r x y ( m ) = ∑ n = − ∞ ∞ x ( n ) y ∗ ( n − m ) r_{xy}(m)=\sum_{n=-\infty}^{\infty}x(n)y^*(n-m) rxy(m)=∑n=−∞∞x(n)y∗(n−m)
- 注意
- 相关运算没有翻折的步骤
- 当y(n)为复数序列时,需要取共轭
- 不满足交换律
圆周相关
- 如果
x
1
(
n
)
x_1(n)
x1(n)和
x
2
(
n
)
x_2(n)
x2(n)都是长度为N的有限长序列
并且: D F T [ x 1 ( n ) ] = X 1 ( k ) , D F T [ x 2 ( n ) ] = X 2 ( k ) , R x y ( k ) = X 1 ( k ) X 2 ∗ ( k ) 则: r x y ( m ) = I D F T [ R x y ( k ) ] = [ ∑ n = 0 N − 1 x 1 ( n ) x 2 ∗ ( ( n − m ) ) N ] R N ( m ) = [ ∑ n = 0 N − 1 x 2 ∗ ( m ) x 1 ( ( n + m ) ) N ] R N ( m ) 定义为 x 1 ( n ) 和 x 2 ( n ) 的圆周相关 \begin{aligned} &并且:DFT[x_1(n)]=X_1(k),DFT[x_2(n)]=X_2(k),R_{xy}(k)=X_1(k)X_2^*(k) \\ &则:r_{xy}(m)=IDFT[R_{xy}(k)]=[\sum_{n=0}^{N-1}x_1(n)x_2^*((n-m))_N]R_N(m)=[\sum_{n=0}^{N-1}x_2^*(m)x_1((n+m))_N]R_N(m) \\ &定义为x_1(n)和x_2(n)的圆周相关 \end{aligned} \\ 并且:DFT[x1(n)]=X1(k),DFT[x2(n)]=X2(k),Rxy(k)=X1(k)X2∗(k)则:rxy(m)=IDFT[Rxy(k)]=[n=0∑N−1x1(n)x2∗((n−m))N]RN(m)=[n=0∑N−1x2∗(m)x1((n+m))N]RN(m)定义为x1(n)和x2(n)的圆周相关 - 一般地,如果两个有限长序列的长度为 N 1 , N 2 N_1,N_2 N1,N2,且满足 N 1 ≥ N 2 N_1 \ge N_2 N1≥N2,则圆周相关的前 N 1 − N 2 + 1 N_1-N_2+1 N1−N2+1个点,与线性相关的结果一致