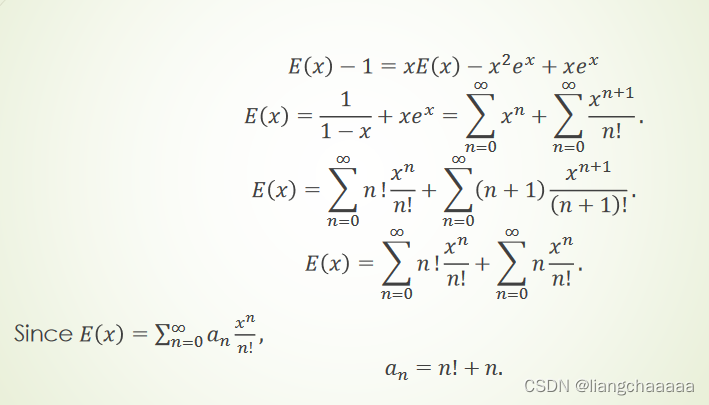一、前言

嵌套是指在一个事物中包含另一个事物，而递归是一种特殊形式的嵌套，其中一个事物包含自身。

递归就是一种嵌套的形式，递归函数解决问题时嵌套调用自身。递归的核心思想是通过反复应用相同的过程来解决问题，每一次调用都在规模上比上一次调用更小，直到达到基本情况从而终止递归。
递归是一种强大而优雅的技术，它能够将复杂的问题分解成更小的子问题来解决，递归和数学归纳法有密切的关系，递归可以被看作是数学归纳法在编程中的一种具体应用。
在这里插入图片描述

二、递归初步理解

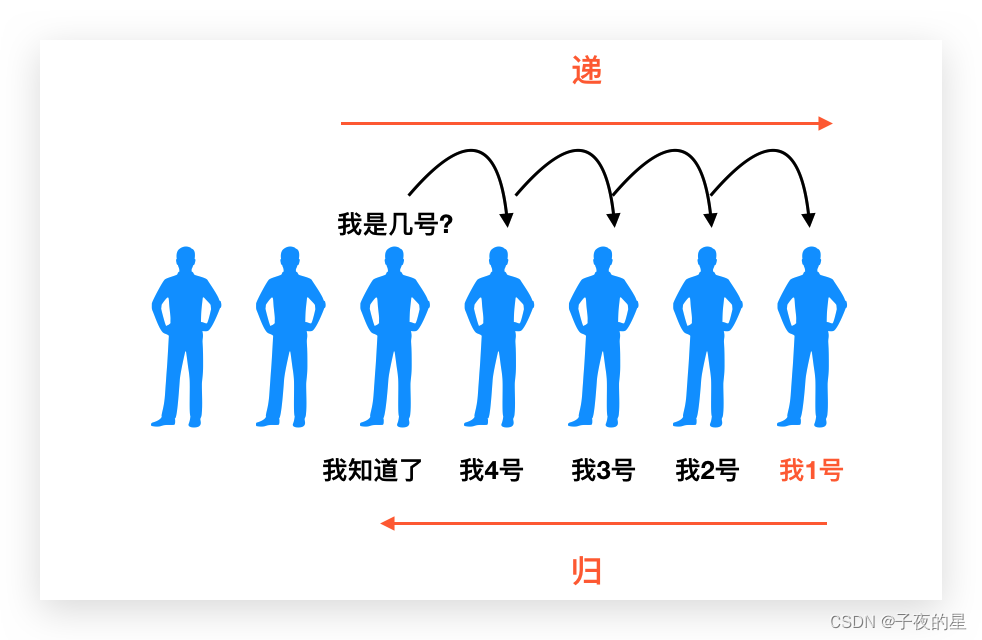
递归 = 递推 + 回归
递归是指函数直接或间接地调用自身的过程。递归函数通常在满足基本条件时停止调用自身，从而避免无限循环。递归的思想是将一个大问题分解成一个或多个相同的较小问题，直到问题简化到可以直接解决为止。
在这里插入图片描述

1、数学归纳法

数学归纳法的核心思想是：如果一个性质对于某个数成立，而且可以证明如果对于任何数n该性质成立就能推导出对于n+1也成立，那么这个性质就对所有正整数成立。

数学归纳法主要包括两个步骤：

基础步骤：首先要证明该性质对于初值（通常是1或0）成立。
归纳步骤：然后要假设性质对于某个数n成立（这被称为归纳假设），并证明这个假设就能推导出该性质对于n+1也成立。

我们可以看如下一个数学归纳法的例子，
$用数学归纳法证明：\sum_{i=1}^{n} i = \frac{n*(n + 1)}{2}。$
用数学归纳法来证明：

先证明对于N=1成立。
再证明N>1时：假设对于N-1成立，那么对于N成立。

2、递归的设计

将上面这个数学归纳法的问题，设计为递归解决，应该怎么解决呢？

int sum(int n){
    if(n==1)
        return 1;	//边界条件：n==1
    else
        return sum(n-1)+n;	//利用sum(n-1)的值，计算sum(n)的值
}

在使用代码解决上面这个问题的时候，我们首先是实现了边界条件，这个对于的不就是数学归纳法中证明N=1的时候成立嘛？

其次， return sum(n-1)+n;这段代码的底层逻辑是假设该递归函数调用的返回值是正确的，而这个假设，就是对应了数学归纳法中的归纳步骤。

在数学归纳法中，我们证明了性质对于一个初始值（通常是1或0）成立。在递归中，我们则定义了一个或多个基本情况，这些情况可以直接解决，无需递归。数学归纳法的归纳步骤和递归的递归步骤都是解决过程的主体部分。在数学归纳法中，我们假设性质对于某个值n成立，然后证明该性质对于n+1也成立。在递归中，假设我们能够解决比当前问题更小的问题，然后通过这些更小的问题来解决当前的问题。

我们可以简单的总结一下递归函数的设计方法：

确定递归函数的参数和返回值：首先，你需要明确递归函数的输入（参数）和输出（返回值）是什么。
确定边界情况：边界情况是递归函数的终止条件。你需要明确当参数满足什么条件时，函数可以直接返回结果，而无需进一步递归。
确定递归情况：递归情况是函数如何调用自身的部分。在这一步，你需要考虑如何将大问题分解成小问题，然后用递归的方式解决这些小问题。

3、递归的练习

Ⅰ、路飞吃桃

题目链接：路飞吃桃

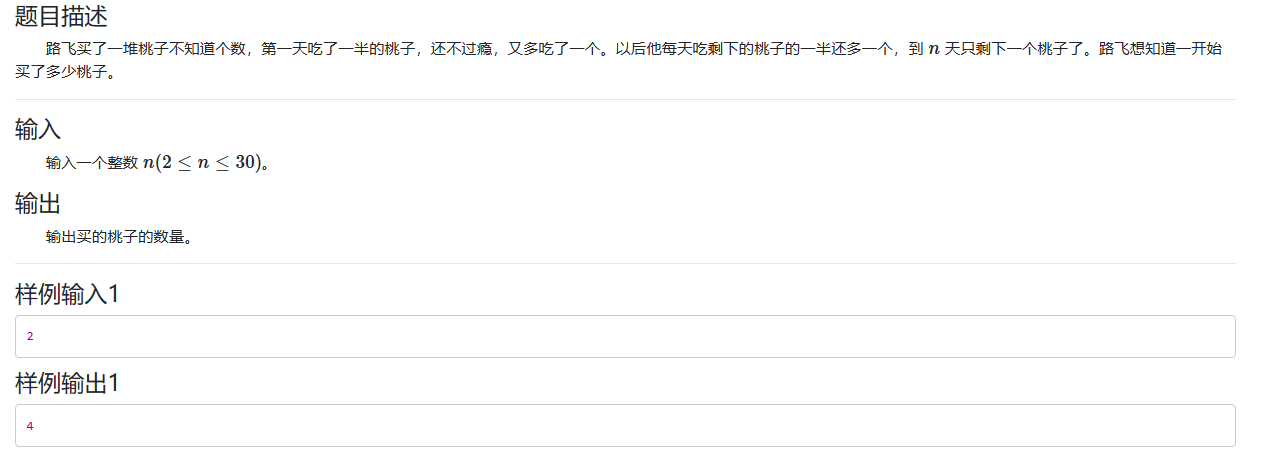
当我们使用递归解决这个问题时，我们可以从第n天开始反向计算。

边界情况：因为题目中已经说明了到第n天时只剩下一个桃子，所以在n=1时，桃子的数量为1。
递归情况：对于第n天，桃子的数量可以根据第n+1天的数量计算。在第n天，桃子的数量是(第n+1天的桃子数量 + 1) * 2。

#include<stdio.h>
int f (int n )  // 确定递归函数的参数和返回值
{
	if(n==1)	//确定边界情况
		return 1; 
	else		//确定递归情况
		return (f(n-1)+1)*2;
}
int main ()
{
	int n = 0;
	scanf("%d",&n);
	printf("%d",f(n));
	return 0;
}

Ⅱ、弹簧版

题目链接：弹簧板

确定递归函数的参数和返回值：递归函数需要接受弹簧板的跳跃能力列表、当前弹簧板的索引和弹簧板的总数作为参数，并返回小球弹跳出去的总次数。
确定基本情况：我们首先需要确定基本情况，即递归函数的终止条件。在这个问题中，如果当前弹簧板超出了弹簧板范围（即当前弹簧板的索引大于等于弹簧板的总数），那么小球无法再继续弹跳，返回0次弹跳。
确定递归情况：在递归情况中，我们将计算从当前弹簧板弹跳出去的总次数。根据题目的描述，我们可以通过当前弹簧板的索引和弹簧板的跳跃能力列表来计算下一次弹跳的弹簧板索引。然后，递归调用函数，并返回1加上从下一个弹簧板开始弹跳出去的总次数。

#include <stdio.h>
int countBounces(int springs[], int currentSpring, int numSprings) {
    // 边界情况：如果当前弹簧板超出范围，返回0次弹跳
    if (currentSpring >= numSprings) {
        return 0;
    }
    // 递归情况：计算从当前弹簧板弹跳出去的次数
    int nextSpring = currentSpring + springs[currentSpring];
    return 1 + countBounces(springs, nextSpring, numSprings);
}
int main() {
    int numSprings;
    scanf("%d", &numSprings);
    int springs[numSprings];
    for (int i = 0; i < numSprings; i++) {
        scanf("%d", &springs[i]);
    }   
    int startSpring = 0;  // 从1号弹簧板开始
    int totalBounces = countBounces(springs, startSpring, numSprings);
    printf("%d\n", totalBounces);
    return 0;
}

Ⅲ、反转链表

题目链接：反转链表

【常规解法】

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
    ListNode new_head,*p = head,*q;
	new_head.next = NULL;
	while(p){
			q = p->next;
			p->next = new_head.next;
            new_head.next = p;
			p=q;
	}
	return new_head.next;
    }
};

【递归解法】

边界情况：如果 head == NULL 或者 head->next == NULL，这表示链表为空或者链表只有一个节点，无需反转，直接返回 head。

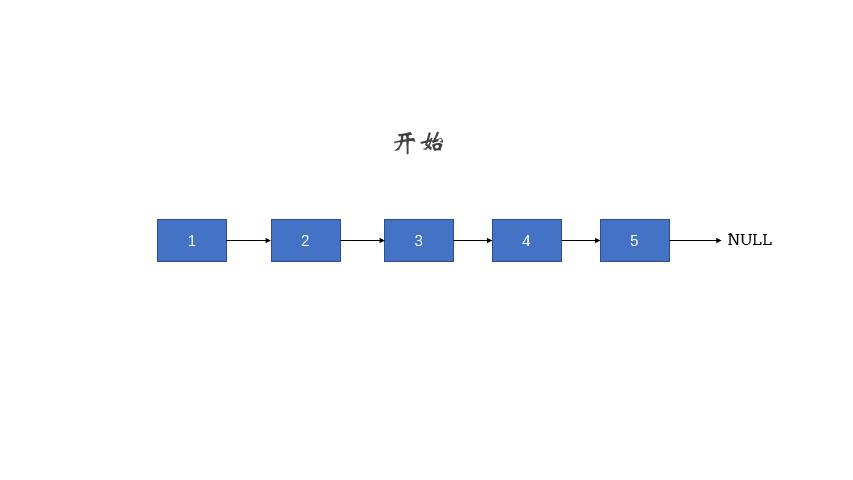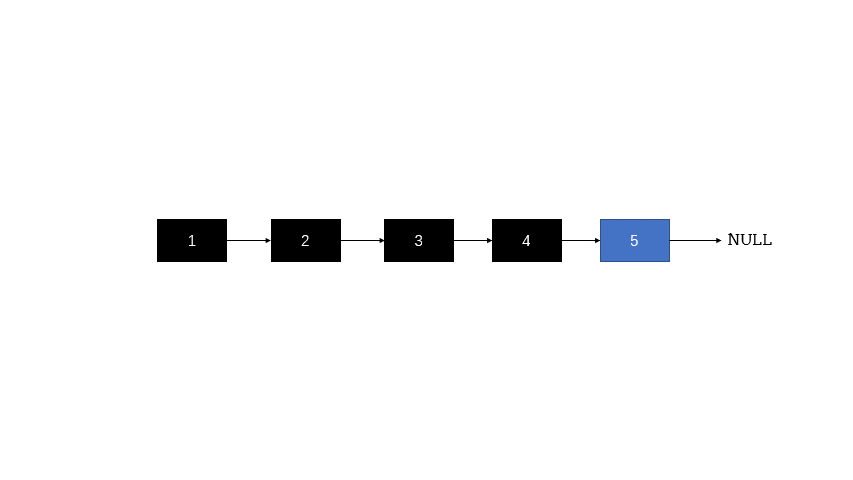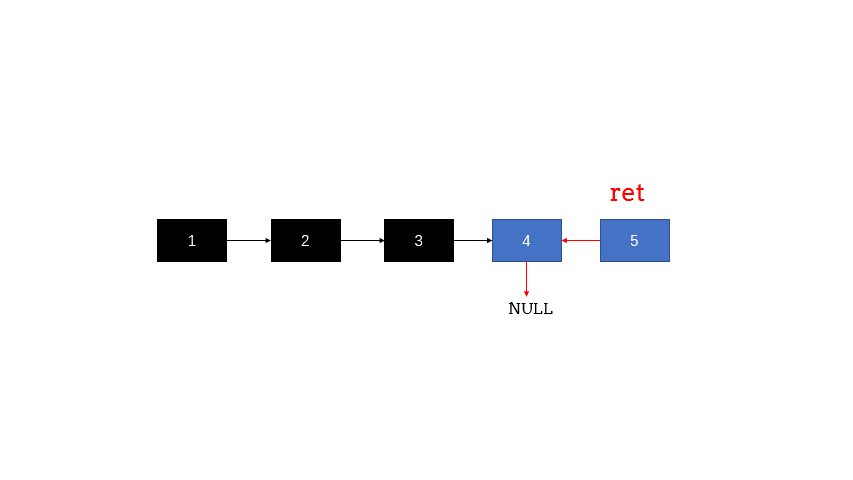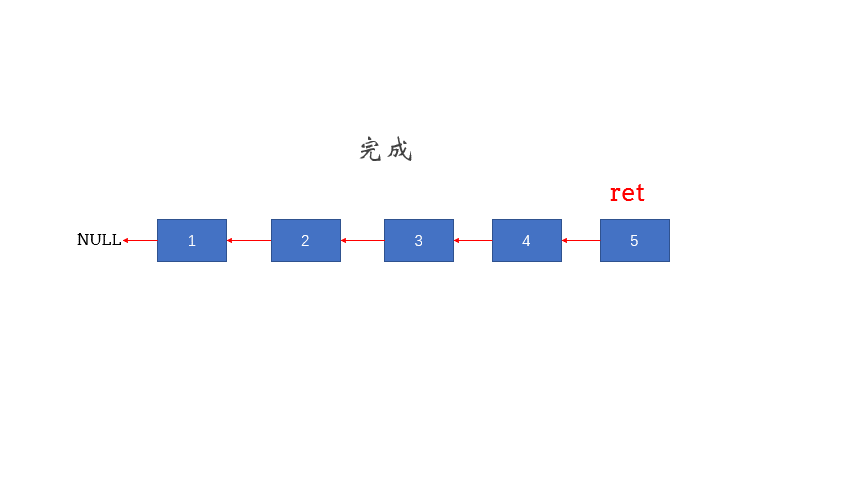
递归步骤：如果链表有多个节点，那么首先通过调用 reverseList(head->next) 进行递归，这个调用会返回反转后的链表头节点（记作 ret）。需要注意的是，此时 head->next 还是指向原链表的下一个节点，这个节点在反转后的链表中是最后一个节点。然后执行 head->next->next = head，这会让 head 的下一个节点的 next 指针指向 head，即实现了局部的反转。最后执行 head->next = NULL，断开原 head 和 head->next 之间的链接，这是因为 head 在反转后的链表中应当是最后一个节点，所以 head->next 应当指向 NULL。最后返回 ret，即反转后的链表的头节点。

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if (head == NULL || head->next == NULL) {
            return head;
        }
        ListNode* ret = reverseList(head->next);
        head->next->next = head;
        head->next = NULL;
        return ret;
    }
};

三、递归的深层理解

1、栈帧结构

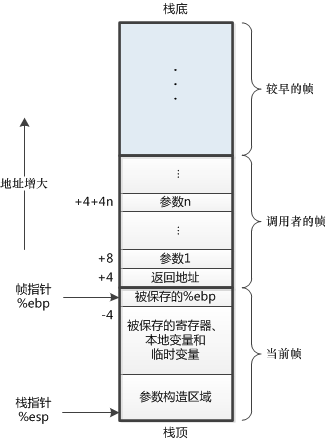
递归允许一个函数直接或间接地调用自己，这种调用方式表现为一种层次结构：每次递归调用都会创建一个新的函数实例，这个新的函数实例处理问题的一部分，并可能进一步调用自身。从底层来看，当一个函数调用自身时，操作系统会为这次函数调用分配一段内存，这段内存称为栈帧。

帧是指为一个函数调用单独分配的那部分栈空间。

比如，当运行中的程序调用另一个函数时，就要进入一个新的栈帧，原来函数的栈帧称为调用者的帧，新的栈帧称为当前帧。被调用的函数运行结束后当前帧全部收缩，回到调用者的帧。

栈帧的创建和销毁是通过栈指针来实现的。栈指针指向当前栈帧的顶部，当一个新的函数调用发生时，栈指针会向下移动，为新的栈帧腾出空间。而当函数执行完毕后，栈指针会向上移动，销毁当前的栈帧。栈帧结构的使用使得函数调用和返回过程可以按照嵌套的方式进行，每个函数都有自己的独立空间来保存参数、局部变量等信息，从而实现了程序的模块化和递归调用。

%ebp是帧指针，它总是指向当前帧的底部；

%esp是栈指针，它总是指向当前帧的顶部。

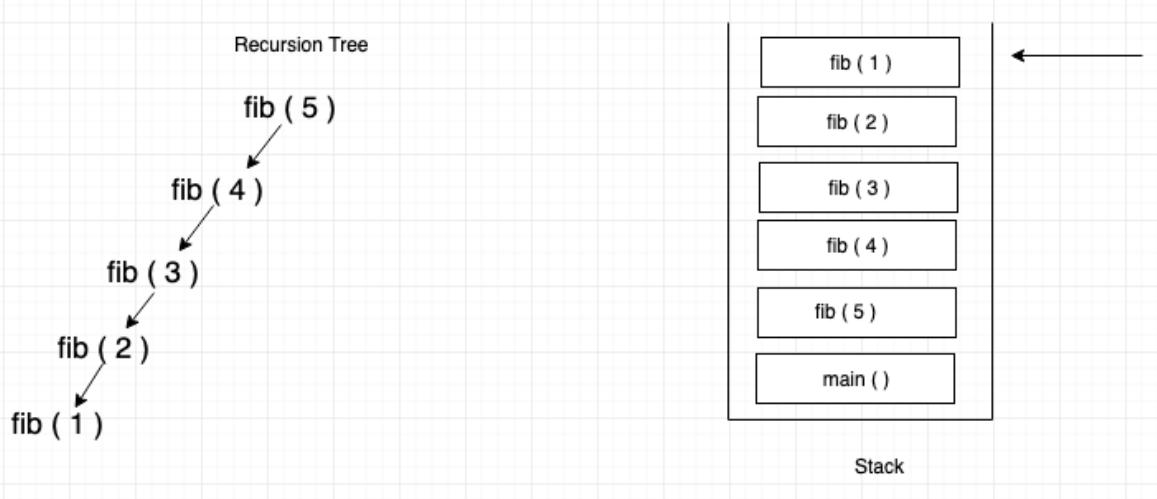
2、递归与栈

递归的底层机制是栈。

这是因为栈在计算机中用于管理函数调用和返回的过程。当一个函数被调用时，会创建一个新的栈帧，栈帧用于存储函数的局部变量、参数和其他相关信息。这个新的栈帧用于存储递归调用的函数的局部变量和参数。每个递归调用都会在调用栈中创建一个新的栈帧，形成一种嵌套的结构。这样，调用栈就能够记录递归调用的顺序和相关的上下文信息。递归的终止条件决定了递归的结束点。