0. 简介

作为路径规划而言，不单单有单个机器人自主路径规划，近年来随着机器人行业的兴起，多机器人自主路径规划也越来越受到关注，对于多智能体寻路(MAPF)。一般的操作会给定一个地图、机器人集群、以及它们的初始位置和目的地，MAPF会最终输出一组没有碰撞的路径，用于控制机器人集群完成运动。《Iterative Refinement for Real-Time Multi-Robot Path Planning》文中认为迭代细化MAPF是可取的，原因有三:1)多智能体优化是棘手的，2)次优解可以立即获得，3)在线场景中需要考虑的时间有限，所以要求MAPF是实时规划的。

文中的方案使用次优MAPF求解器来快速获得初始解，然后迭代两个过程:1)选择代理子集，2)使用最优MAPF求解器来优化所选代理的路径，同时保持其他路径不变。由于单个最优求解器只会优化所选代理机器人的路径，因此该方案可以快速生成足够有效的解决方案，同时提供高可伸缩性。相应的代码也在Github上开源了，可以这么说，这套方法还是很有意义的，

1. 文章贡献

1. 文中提出了一个通用的框架，基于现有求解器的有效组合可以快速的提供anytimeMAPF求解。 文中的框架首先使用次优MAPF求解器快速获得初始可行解，然后使用最优MAPF求解器找到良好的邻域解。精确地说，该框架通过选择一组代理并使用最优求解器来细化它们的路径，同时保持其他路径固定，迭代地细化解决方案。尽管在细化过程使用了最优求解器，但是每次细化都能快速完成，因为它解决的是一个子问题，其大小取决于选择的代理机器人数量，通常比原问题小得多。我们还提出了合理的候选人，用于选择代理子集。
2. 文中研究了在各种基准测试中该方法的有效性，并经验地发现，在小型实例中，该框架在短时间内几乎收敛到最优，并且即使对于非常大的实例（即大环境和/或许多代理）也保持着高效响应。换句话说，它比先前的技术带来了许多实际优势。
3. 从更广泛的角度来看，我们的研究也可以被看作是解决一个非常大规模的邻域搜索[24]。更接近我们的概念，Balyo等人[25]研究了针对独立于领域的规划问题的局部重新规划，以优化最长时间。它重复以下操作：创建一个子问题，通过基于SAT的技术获得一个最优子解，并用新的解决方案替换原来的部分解决方案。
   

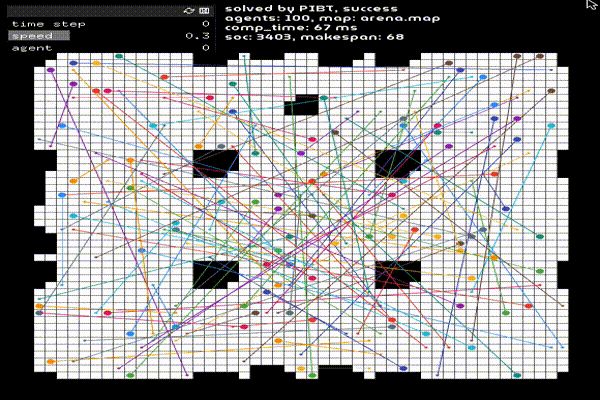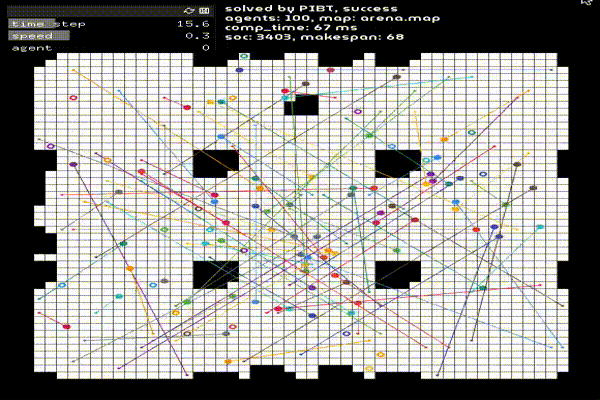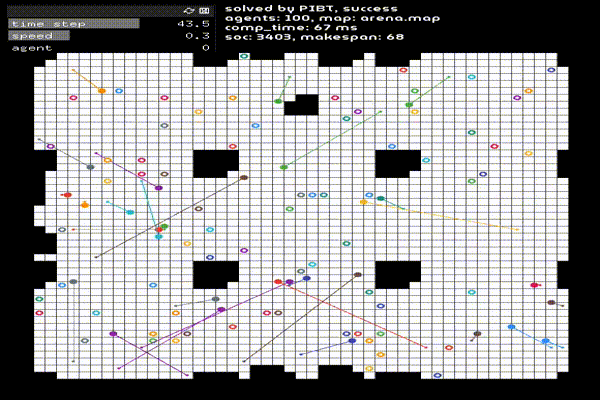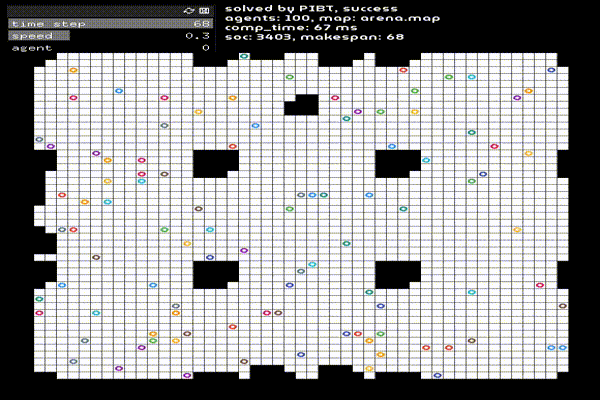
2. 主要框架

该框架首先使用次优MAPF求解器获得初始解决方案，然后迭代地细化解决方案的选定部分，即选定代理子集的路径，使用最优MAPF求解器。我们在算法1中给出了伪代码

下面我们来详细的看一下，第1行输入的是次优求解器快速获得初始可行解决方案。在第二行中，我们称所用的次优MAPF求解器为初始求解器。如果初始求解器未能获得解决方案，则框架以失败告终;否则，开始细化，也就是3-6行里面的内容。细化重复以下两个过程，直到中断:

1. 使用当前解决方案π [第4行]创建修改集M ⊆ A。
2. 使用最优MAPF求解器[第5行]改变M中代理的路径来细化当前解决方案π。我们称这个求解器为细化求解器。细化求解器只改变M中代理的路径；M中代理以外的路径不变。细化继续进行直到中断，例如超时、达到预定迭代次数、不再有改进时、用户中断等。
   最终，框架返回最终解决方案[第7行]。

上文中提到的初始求解器可以是任何次优MAPF求解器，只要它能提供可行解即可。作为细化求解器，最好使用从最优求解器改编的版本。改编很简单；让它为M中的代理规划路径，并将其他代理视为动态障碍。例如，对于CBS算法，只为M中的代理求解MAPF，同时禁止低级别搜索使用M中代理以外的所有空间时间对。确切地说，细化求解器并不局限于最优MAPF求解器（可以使用单机器人的求解器）。要求是细化解决方案从原始解决方案不变差。考虑到M中代理以外的路径成本不变，要求是M中代理的路径成本在细化之前和之后都不会增加。

3. 细化求解器性质与要求

下面有一些性质显然是由对细化求解器的要求所设定的。

3.1 定理1(单调性)：

对于算法1中的每次迭代，解决方案成本都是不增加的。
一个关键点是细化求解器重新计算所选子集M（一部分机器人）中代理的路径，而不是所有代理的集合A（所有机器人）。与直接使用最优求解器解决原问题相比，细化求解器在每次迭代中解决的问题明显小得多，确保框架即使对于大量代理也是可扩展的。同时下面有几种方法来有效的降低计算的时间。

A.提前终止（早停）
即使细化求解器解决的子问题与原问题相比计算量已经是较小的了，但是如果本身的$|M|$仍然太大，细化仍然可能需要很长时间。在这种情况下，最好通过返回当前解决方案来中止当前细化，然后使用新的集合$M$开始新的迭代。标准可以是超时或使用细化求解器中搜索树大小的阈值。

B.局限性
作为一个限制，该框架可能具有局部最小值，并且没有来自最优解的次优性界限。
命题1(没有次优性界限)：考虑最优成本$c^{\ast }$。在算法1中，总是$c\le w{c}^{\ast }$，除非将$A$本身选为修改集$M$，其中$c$是每次迭代中的解决方案成本。
证明：考虑图1中的一个例子。假设初始解决方案将$a_1$分配给顺时针路径(成本：$k$)和$a_2$分配给逆时针路径(成本：1)。当k≥6时，这就不是最优的模型了，因为$a_1$可以采取逆时针路径，并经过$a_2$来移动到目标处（总成本：6）。除非$M\ne A$，否则细化的解决方案不变。假设$w\ge 1$，使得$c\le w{c}^{\ast }$。我们可以取任意$k$，与$w$的存在相矛盾。

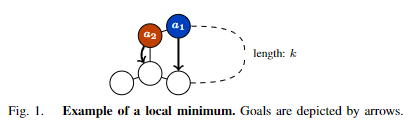
3.2 定理2（局部最小值存在）

根据初始解决方案，除非将A本身选为M，否则可能无法达到最优解。

注意，当$M=A$时，细化求解器必须能够解决原始MAPF问题。

4. 修改集选择

我们从上面可以看到在优化的时候，修改集的选择会影响到整个系统的性能，而如何有效的选择修改集这个就非常重要了。修改集是框架的重要组成部分，其设计会影响计算时间和解决方案质量等性能。本节定义了几个选择规则，以提供合理的候选修改集。

4.1 随机的

一个天真的方法是随机挑选一个代理子集。然后，修改集的大小$M$就是一个用户指定的参数。需要注意的是，大的$M$修改有机会在一次迭代中很大程度上降低成本，但由于子问题变得具有挑战性，因此需要花费时间进行细化。

4.2 单一代理

这个规则总是选择一个单一的代理，因为$M$可以被视为前一个规则（随机）的一个特例。即使只有一个代理，成本也可能因细化而降低。在这种情况下，细化只是一个单一代理的路径寻找问题，可以在没有$MAPF$求解器的情况下有效地计算出来，例如，通过$A^{\ast }$来计算即可，可以简化为一个机器人在其余障碍物（机器人）中规划出来的最优路径。

4.3 着重目标

考虑图2中的一个例子。假设当前的解决方案是$\pi 1=(v2,v3,v6,v3,v3)$ 和$\pi 2=(v1,v2,v3,v4,v5)$ 。代理人$a_1$不能实现更短的路径，因为代理人$a_2$在第2个时间步长(第三个值)使用了$a_1$的目标（即v3）。一般来说，对于$a_i$来说，理想成本$dist({\pi }_i[0],g_i)$和实际成本成本$(a_i,\pi )$之间存在差距的一个原因可能是另一个代理人$a_j$在时间步骤$t\ge dist({\pi }_i[0],g_i)$时使用了$a_i$的目标（即$g_i$）。至少在$t$之前，$a_i$不能到达$g_i$并留在那里。在这种情况下，需要联合完善$a_i$和$a_j$的路径。这一观察促使我们创建了一个简单的规则，将当前的解决方案$\pi$和一个代理$a_i$作为输入。

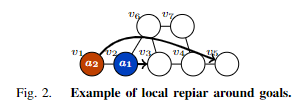
4.4 围绕目标的局部修复

这是上一条规则（关注目标）的一个特例。再次假设图2的例子；$\pi 1=(v2,v3,v6,v3,v3)$，$\pi 2=(v1,v2,v3,v4,v5)$。在聚焦目标（focus-at-goals）中，$a_1$的$M$是 { a 1 , a 2 } \{a_1, a_2\} {a1​,a2​}，因此，细化求解器必须用两个代理解决一个子问题；然而，这种努力可以减少。考虑为$a_1$获得一个更好的路径，忽略${\pi }_2$。在这个例子中，通过目标周围的局部修复获得一条新的路径，不需要搜索；$(v2,v3,v3,v3,v3)$。接下来，为$a_2$计算一条路径，同时避免与这条新路径和其他代理的路径发生碰撞。如果两条新路径的成本之和小于原始路径，就用新路径替换${\pi }_1$和${\pi }_2$。由于搜索工作量减少，预计细化工作会更快完成。一般来说，当${\pi }_i=（...，g_i，v，g_i，...，g_i）$，其中$v\ne g_i$，而另一个代理$a_j$在该时间步长使用$g_i$时，可以应用这一规则。

4.5 使用MDD

给定一个单一的路径成本$c$，从${\pi }_i[0]$到$g_i$的一组路径可以紧凑地表示为一个多值决策图（MMDD）[35]；一个有向无环图，其中一个顶点是一对位置$v\in V$和一个时间步长$t\in N$。

1. 在该时间段从起点出发的可达位置；
2. 从该时间段到目标的可达位置。
   让MDDc i是一个成本为$c$的$a_i$的MDD，图3显示了两个例子。$MD{D}_1^2$和$MD{D}_1^3$。MDD在MAPF求解器中经常使用[28], [36]。

…详情请参照古月居