📷10.2 图的术语和几种特殊的图
- 1. 基本术语
- 1.1 邻接(相邻)
- 1.2 邻居
- 1.3 顶点的度
- 1.4 孤立点
- 1.5 悬挂点
- 例题
- 2. 握手定理
- 3. 握手定理的推论
- 4. 带有有向边的图的术语
- 4.1 邻接
- 4.2 度——出度 和 入度
- 4.3 例题:
- 5. 定理:入度的和 = 出度的和 = 边数
- 6. 几种特殊的图
- 6.1 完全图 K~n~
- 6.2 圈图 C~n~
- 6.3 轮图 W~n~
- 6.4 n立方体图 Q~n~
- 7. 二分图
- 7.1 判断一个图是否为二分图的定理
- 例题:
- 7.2 完全二分图
本节介绍图论的一些基本词汇。在本节后面部分,当解决许多不同类型的问题时,会使用这些词汇。
1. 基本术语
首先给出描述无向图的顶点和边的一些术语
1.1 邻接(相邻)
若u和v是无向图G中的一条边 e 的端点,则称两个顶点u和v在G里邻接(或相邻)。
这样的边e称为关联顶点u和v,也可以说边e 连接 u 和 v。
1.2 邻居
图G =(V,E)中,顶点v 的所有相邻顶点的集合称为顶点v的邻居,记作N(v)。
若A是V的子集,我们用N(A)表示图G中至少和A中一个顶点相邻的所有顶点的集合。所以N(A)=∪N(v),v∈𝐴
1.3 顶点的度
在无向图中,顶点的度是与该顶点相关联的边的数目。顶点上的环为顶点的度做出双倍贡献,也就是说一个顶点增加一个环,度增加2。
顶点v 的度记成deg(v)
1.4 孤立点
把度为0的顶点称为孤立点。
因此孤立点不与任何顶点相邻。
1.5 悬挂点
顶点是悬挂点,当且仅当它的度是1。
因此悬挂点恰与1个其他顶点相邻。
例题
如图1所示,图G和图H的顶点的度、顶点的邻居是什么? 哪些点是孤立点,哪些点是悬挂点?
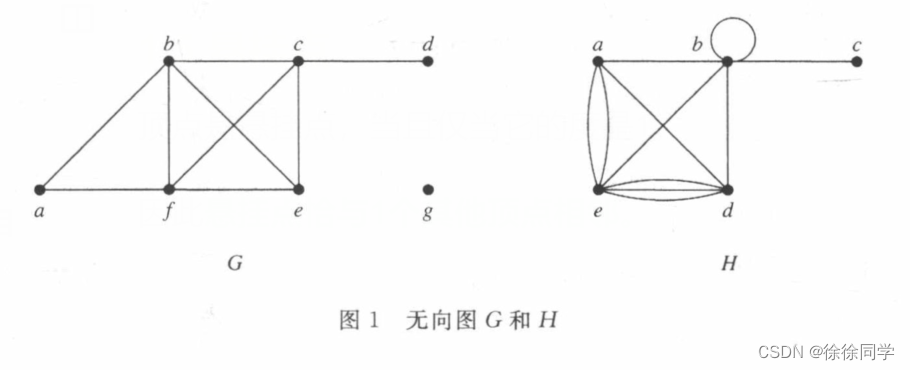
🔴解:
图G:
deg(a)=2,deg( b )=deg( c ) =deg( f )=4,deg( d )=1,deg( e )=3,deg( g )=0
这些顶点的邻居是N( a )={b,f},N ( b )={a,c,e,f),N( c )={b,d,e,f),N( d )={ c },N( e )={b,c,f),N( f )={a,b,c,e} 和N( g )= ∅
图G的顶点g是孤立点,顶点d是悬挂点
图H:
deg( a )=4,deg( b )=deg( e )=6,deg( c )=1,deg( d )=5。
这些顶点的邻居是N( a )={b,d,e},N( b )={a,b,c,d,e},N( c )={b},N( d )={a,b,e}和N( e )={a,b,d}。
图H的顶点c是悬挂点,没有孤立点
2. 握手定理

例题:
一个具有10个顶点且每个顶点的度都为6的图,有多少条边?
🔴解:
因为顶点的度之和是6·10=60,所以2m=60,其中m是边的条数。因此m=30
3. 握手定理的推论
定理:无向图有偶数个度为奇数的顶点。( 偶数包含0 )
4. 带有有向边的图的术语
带有有向边的图的术语反映出有向图中的边是有方向性的
4.1 邻接
定义:当(u,v)是带有有向边的图G的边时,我们称u邻接到v,而且说v从u邻接。
顶点u称为 (u, v) 的起点,v称为 (u, v) 的终点。
注意,环的起点和终点是相同的。
4.2 度——出度 和 入度
因为带有有向边的图 的边是有序对,所以这时顶点度的定义细化成把这个顶点作为起点和作为终点的不同的边数。
入度定义:在带有有向边的图里,顶点v的入度,记作deg-(v),是以v作为终点的边数。
出度定义:顶点v的出度,记作deg+(v),是以v作为起点的边数
注意,顶点上的环对这个顶点的入度和出度的贡献都是1。
4.3 例题:
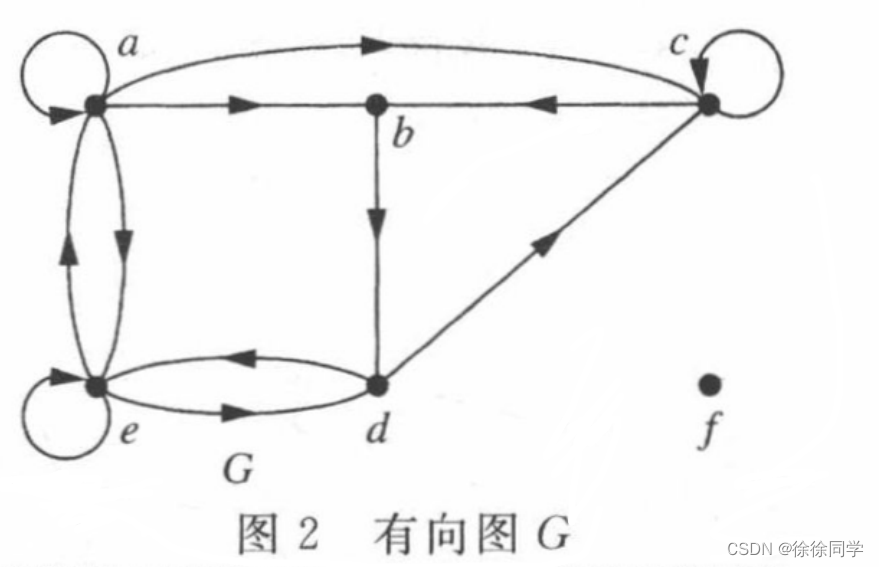
例4:求出图2所示带有向边的图G中每个顶点的入度和出度
🔴解:
在图G中,
入度是:deg-(a) = 2, deg-(b) = 2,deg-( c) = 3,deg- (d) = 2,deg-(e) = 3,deg-(f) = 0。
出度是:deg+(a) = 4,deg+ (b)=1,deg+( c) = 2,deg+ (d) = 2,deg+(e) = 3,deg+ (f) = 0。
因为每条边都有一个起点和一个终点,所以在带有向边的图中,所有顶点的入度之和与所有顶点的出度之和相同。这两个和都等于图中的边数。把这个结果表述成下面的定理。
5. 定理:入度的和 = 出度的和 = 边数
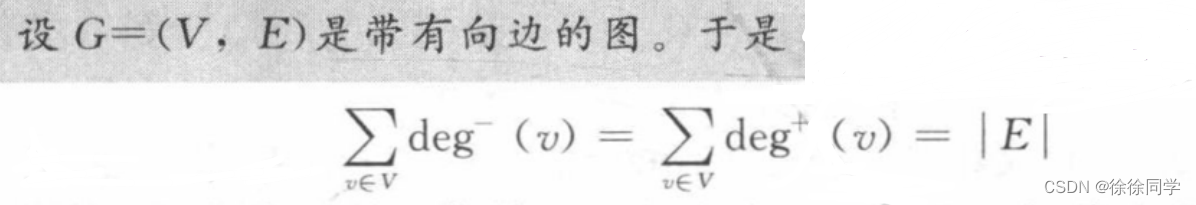 带有向边的图有许多性质是不依赖于边的方向的。
带有向边的图有许多性质是不依赖于边的方向的。
因此,忽略这些方向经常是有用处的。忽略边的方向后得到的无向图称为基本无向图。带有向边的图与它的基本无向图有相同的边数。
6. 几种特殊的图
6.1 完全图 Kn
完全图:n个顶点的完全图记作Kn,是在每对不同顶点之间都恰有一条边的简单图
非完全图:至少有一对不同的顶点不存在边相连的简单图
含n个顶点的完全图的边数:n · (n - 1)/2,即C2n
为什么K~n~表示完全图呢? 一些消息来源称,这个符号中的字母K代表德语单词komplett,但完全图的德文名称vollständigerGraph不包含字母K,其他来源则表示符号表示KazimierzKuratowski图论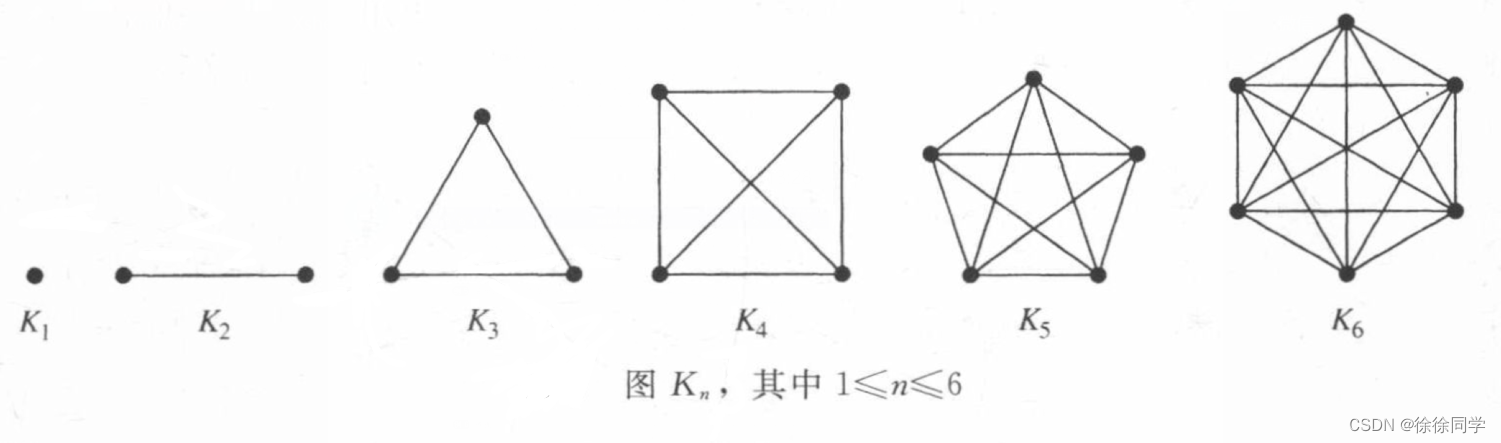
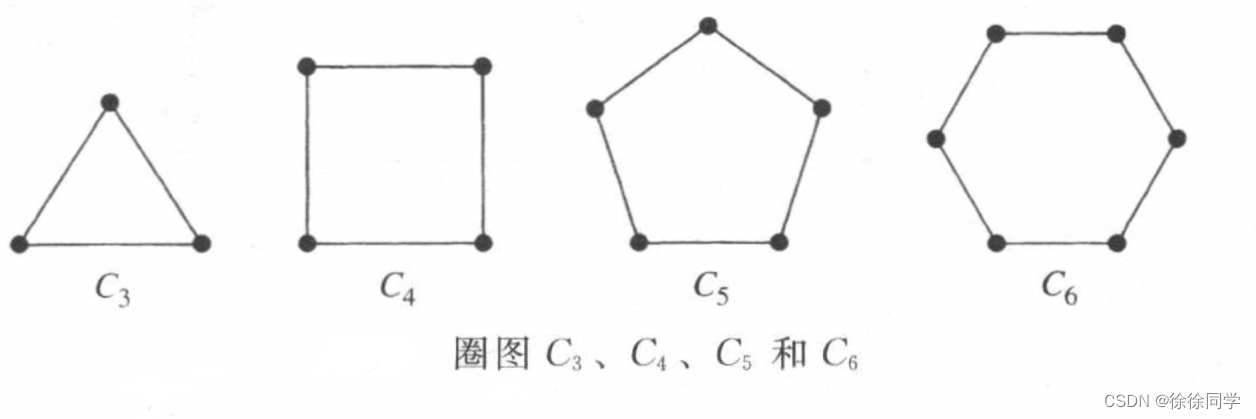
6.2 圈图 Cn
圈图:圈图Cn(n ≥3 )是由n个顶点v1,v2,···,vn以及边{v1,v2},{v2,v3},···,{vn-1,vn},{vn,v1}组成的
Cn,C表示circle嘛
含n个顶点的圈图的边数:n
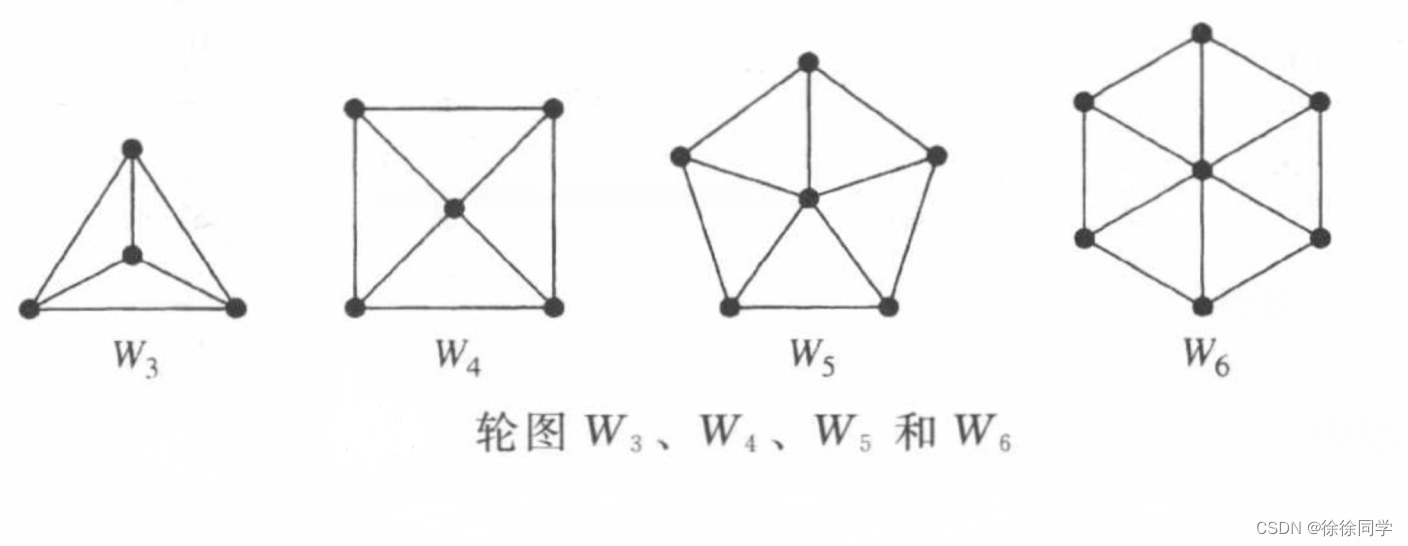
6.3 轮图 Wn
轮图:当给圈图Cn(n ≥3 ),添加另一个顶点,并把这个新顶点与Cn中的n个顶点逐个连接时,就得到轮图Wn
注意,轮图Wn的下标n是轮圈上的顶点数,不是总顶点数(总顶点数是n+1,加上中心的那个顶点)
Wn,W表示wheel(轮)嘛
含n个顶点的轮图的边数:2 ·(n - 1)
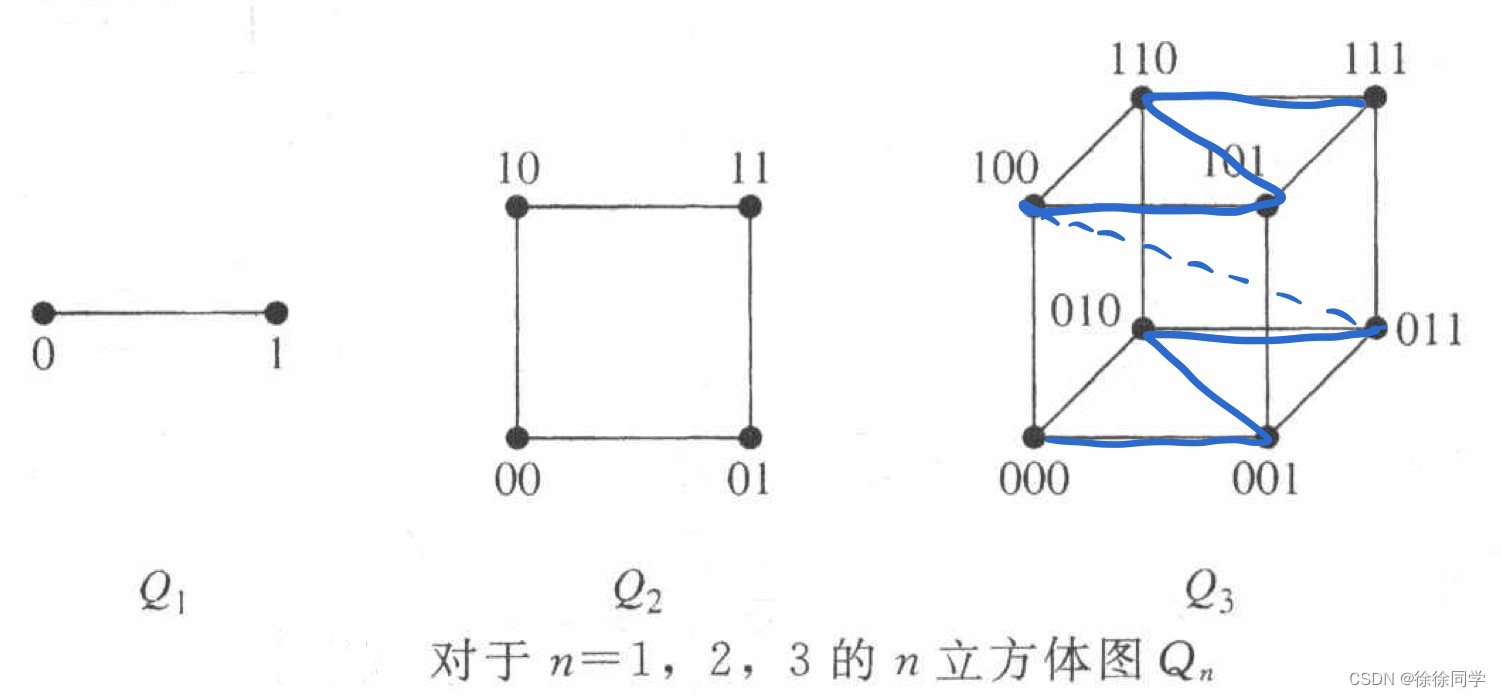
6.4 n立方体图 Qn
n立方体图:n立方体图记作Qn,是用顶点表示2n个长度为n 的比特串的图。
注意,两个顶点相邻 iff 它们所表示的比特串恰恰有一位不同。
含n个顶点的n立方体图的边数:2n
7. 二分图
定义:若把简单图G的顶点集分成两个不相交的非空集合V1和 V2, 使得图中的每一条边都连接V1中一个顶点和V2中的一个顶点(因此G中没有一条边会连接V1中两个顶点或V2中两个顶点),则G称为二分图。
当此条件成立时称(V1,V2)为G的顶点集的一个二部划分。
7.1 判断一个图是否为二分图的定理
定理:一个简单图是二分图 iff 能够对图中的每个顶点赋予两种不同的颜色,并使得没有两个相邻的顶点被赋予相同的颜色。
例题:
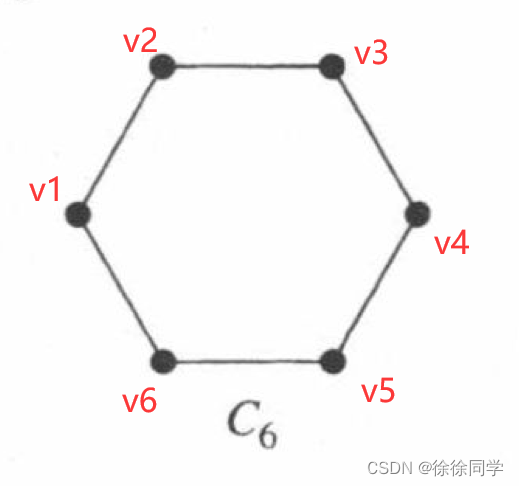
例1:说明C6是二分图
🔴解:
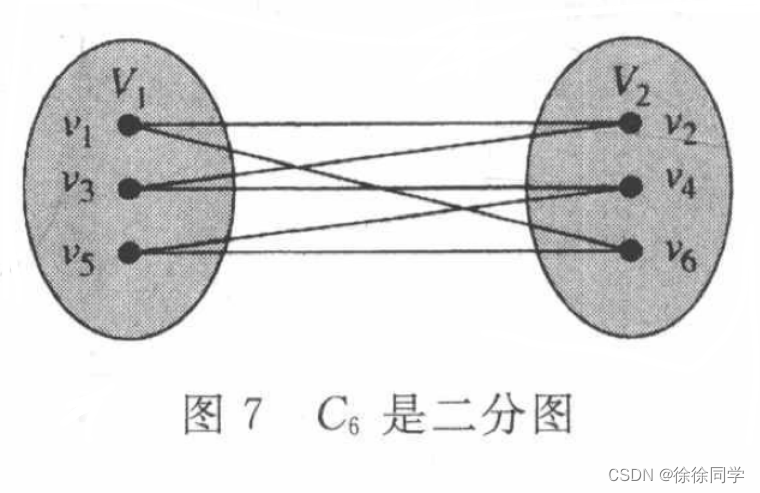
C6是二分图,因为它的顶点集被分成两个集合V1 = { v1, v3, v5}和V1 = { v2, v4, v6},C6的每一条边都连接V1中的一个顶点和V2中的一个顶点
例2:说明K3不是二分图
🔴解:
若把K3内顶点集分成两个不相交的集合,则两个集合之一必然包含两个顶点。假如这个图是二分图,那么这两个顶点就不能用边连接,但是在K3中每一个顶点都有边连接到其他每个顶点。
上面这两个例题当然也可以直接用染色法,很容易判断
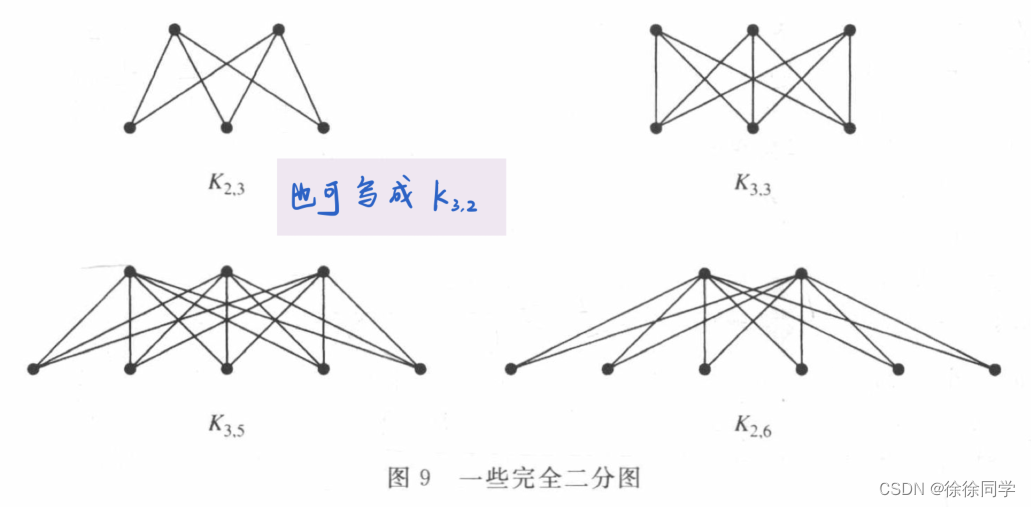
7.2 完全二分图
完全二分图 Km,n 是顶点集划分成分别含有 m 和 n 个顶点的两个子集的图,并且两个顶点之间有边 iff 一个顶点属于第一个子集,而另一个顶点属于第二个子集。