1. 关联式容器 在初阶阶段，我们已经接触过STL中的部分容器，比如：vector、list、deque、 forward_list(C++11)等，这些容器统称为序列式容器，因为其底层为线性序列的数据结构，里面 存储的是元素本身。那什么是关联式容器？它与序列式容器有什么区别？
关联式容器也是用来存储数据的，与序列式容器不同的是，其里面存储的是结构的键值对，在数据检索时比序列式容器效率更高。
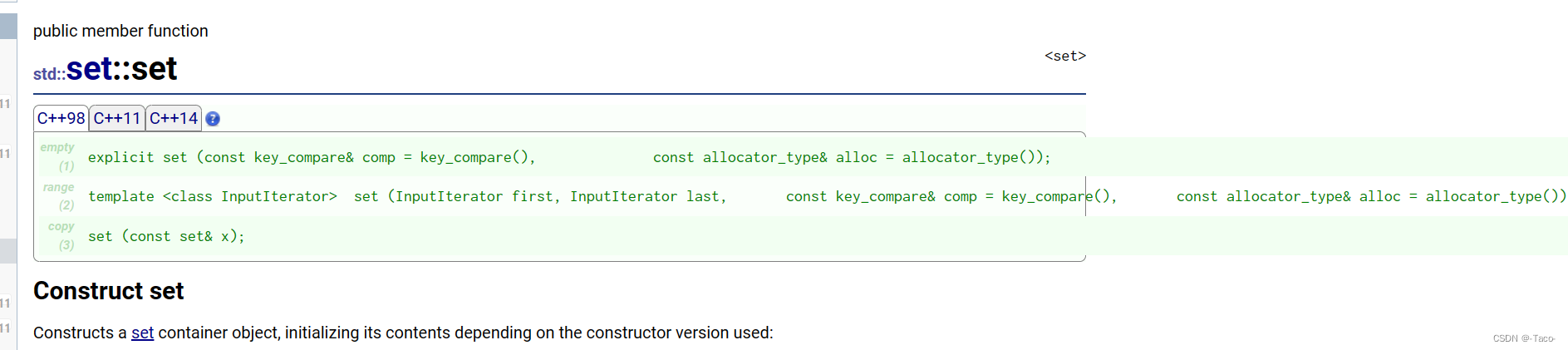
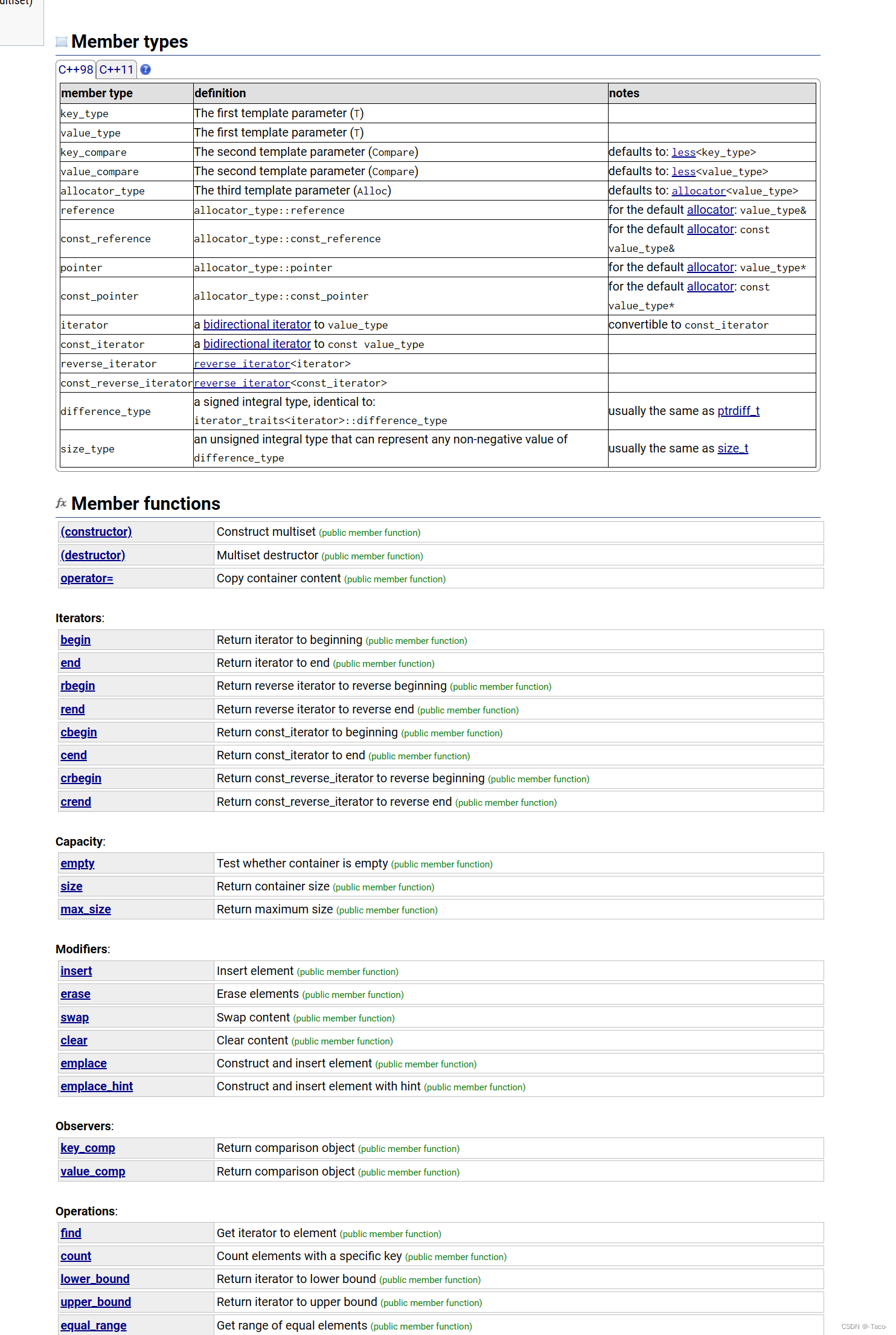
set的介绍:
1. set是按照一定次序存储元素的容器
2. 在set中，元素的value也标识它(value就是key，类型为T)，并且每个value必须是唯一的。 set中的元素不能在容器中修改(元素总是const)，但是可以从容器中插入或删除它们。
3. 在内部，set中的元素总是按照其内部比较对象(类型比较)所指示的特定严格弱排序准则进行 排序。
4. set容器通过key访问单个元素的速度通常比unordered_set容器慢，但它们允许根据顺序对 子集进行直接迭代。
5. set在底层是用二叉搜索树(红黑树)实现的。
set的构造：
set的容量：
bool empty ( ) const 检测set是否为空，空返回true，否则返回true
size_type size() const 返回set中有效元素的个数
5. set修改操作：
pair<iterator, bool> insert(const value_type& x)在set中插入元素x，实际插入的是<x, x>构成的
键值对，如果插入成功，返回<该元素在set中的位置，true>, 如果插入失败，说明x在set中已经
存在，返回<x在set中的位置，false>
void erase(iterator position) 删除set中position位置上的元素
size_type erase(constkey_type& x) 删除set中值为x的元素，返回删除的元素的个数
void erase(iterator first,iterator last) 删除set中[first, last)区间中的元素
void swap(set<Key, Compare, Allocator>&st);
交换set中的元素
void clear() 将set中的元素清空
iterator find(const key_type& x) const 返回set中值为x的元素的位置
size_type count(const key_type& x) const 返回set中值为x的元素的个数
使用实例：
void test_set_01()
{
//set<int> s;
/*s.insert(4);
s.insert(6);
s.insert(9);
s.insert(15);*/
//插入支持一段迭代器区间，可以使用一个数组传入
vector<int> a = { 1,2,3,6,7,8,9 };
set<int>s(a.begin(), a.end());
/*
* int a[]={1,2,3,5,7,44,67};
* set<int>s(a,a+sizeof(a)/sizeof(int));
*/
//vector,list...也可以这样初始化：
//set<int> s = { 1,2,3,5,8,9,10 };
}
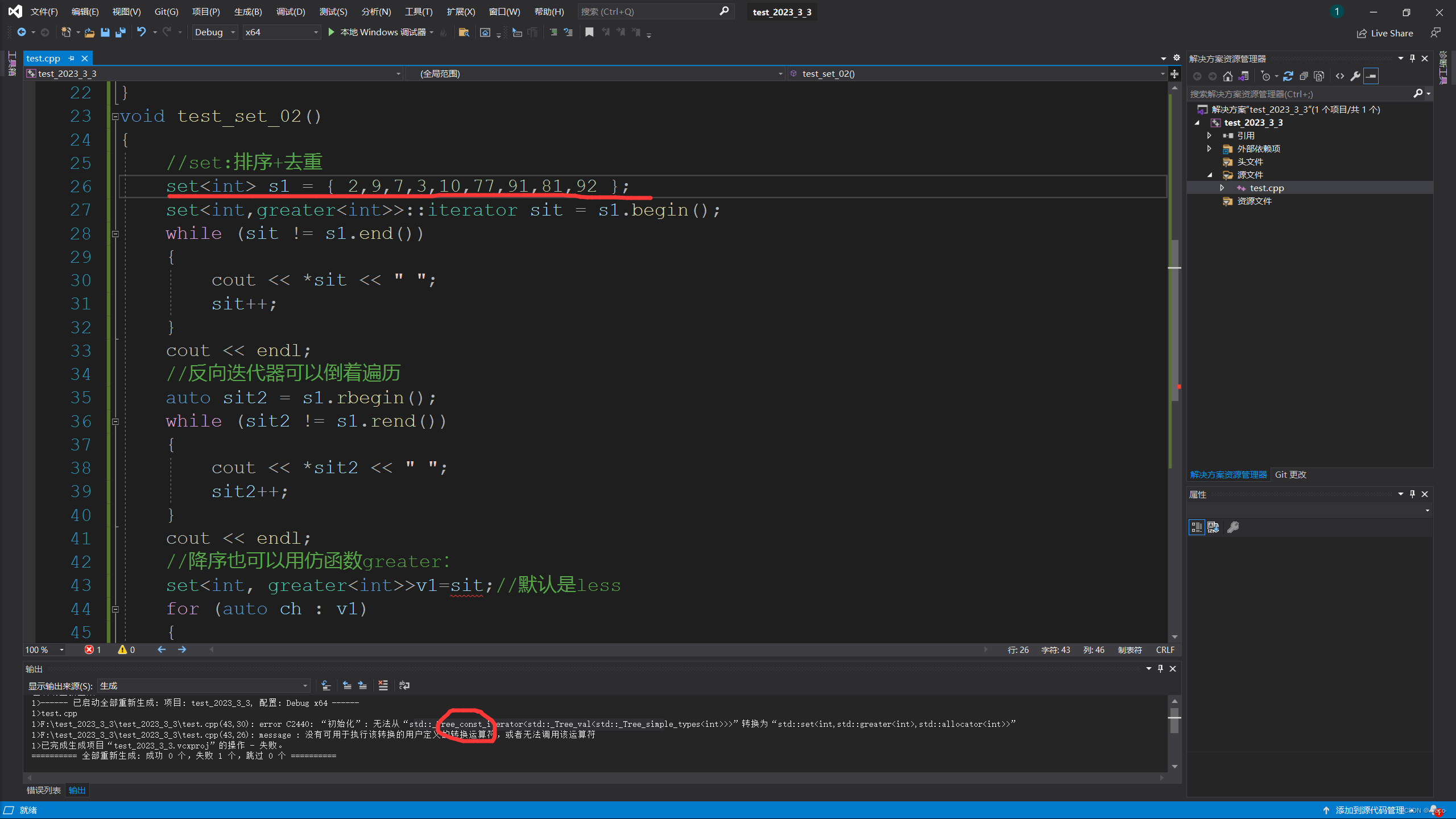
void test_set_02()
{
//set:排序+去重
set<int> s1 = { 2,9,7,3,10,77,91,81,92 };
set<int,greater<int>>::iterator sit = s1.begin();
while (sit != s1.end())
{
cout << *sit << " ";
sit++;
}
cout << endl;
//反向迭代器可以倒着遍历
auto sit2 = s1.rbegin();
while (sit2 != s1.rend())
{
cout << *sit2 << " ";
sit2++;
}
cout << endl;
//降序也可以用仿函数greater：
set<int, greater<int>> v1 = { 1,2,3,44,4,4,5 };//默认是less
for (auto ch : v1)
{
cout << ch << " ";
}
}
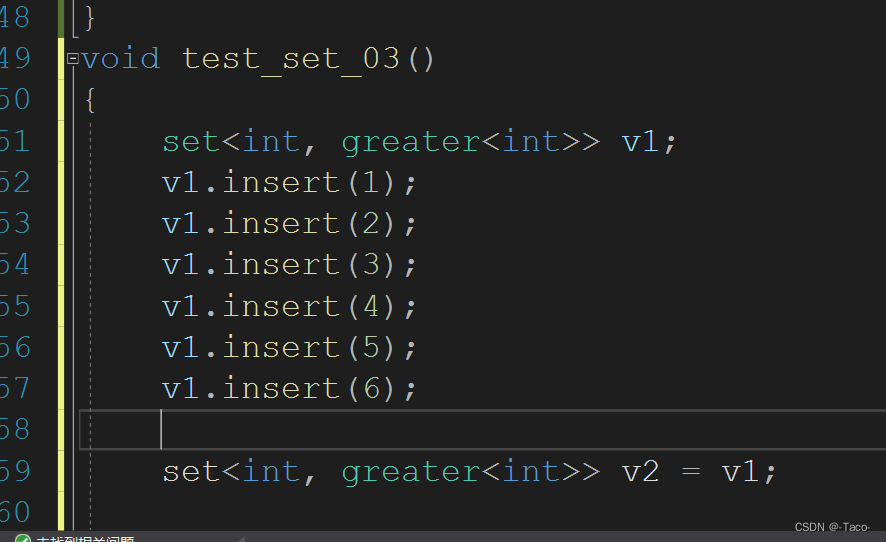
void test_set_03()
{
set<int, greater<int>> v1;
v1.insert(1);
v1.insert(2);
v1.insert(3);
v1.insert(4);
v1.insert(5);
v1.insert(6);
set<int, greater<int>> v2 = v1;
}
void test()
{
set<int, greater<int>>st1;
st1.insert(1);
st1.insert(2);
st1.insert(1);
st1.insert(3);
st1.insert(4);
for (auto ch : st1)
{
cout << ch << " ";
}
cout << endl;
set<int, greater<int>>::iterator s1 = st1.begin();
cout << *s1 << endl;
}
void test_set_04()
{
set<int, greater<int>> s1 = { 1,2,3,4,5,6,7 };
auto f = s1.find(3);
s1.erase(f);
for (auto ch : s1)
{
cout << ch << " ";
}
cout << endl;
}
void test_set_05()
{
set<int> st1 = { 1,23,22,35,33,54,74 };
cout << st1.count(23);
cout << endl;
cout << st1.count(3);
//count可以看这个数是否在树内，如果在输出1，不在输出0；
}
void test_set_06()
{
std::set<int> myset;
std::set<int>::iterator itlow, itup;
for (int i = 1; i < 10; i++) myset.insert(i * 10); // 10 20 30 40 50 60 70 80 90
itlow = myset.lower_bound(35); // ^
itup = myset.upper_bound(60); // ^
cout << "[" << *itlow << "," << *itup << "]" << endl;
myset.erase(itlow, itup); // 10 20 70 80 90
std::cout << "myset contains:";
for (std::set<int>::iterator it = myset.begin(); it != myset.end(); ++it)
std::cout << ' ' << *it;
std::cout << '\n';
//lower_bound返回的是大于等于这个值；
//upper_bound返回的是大于value的值;
}
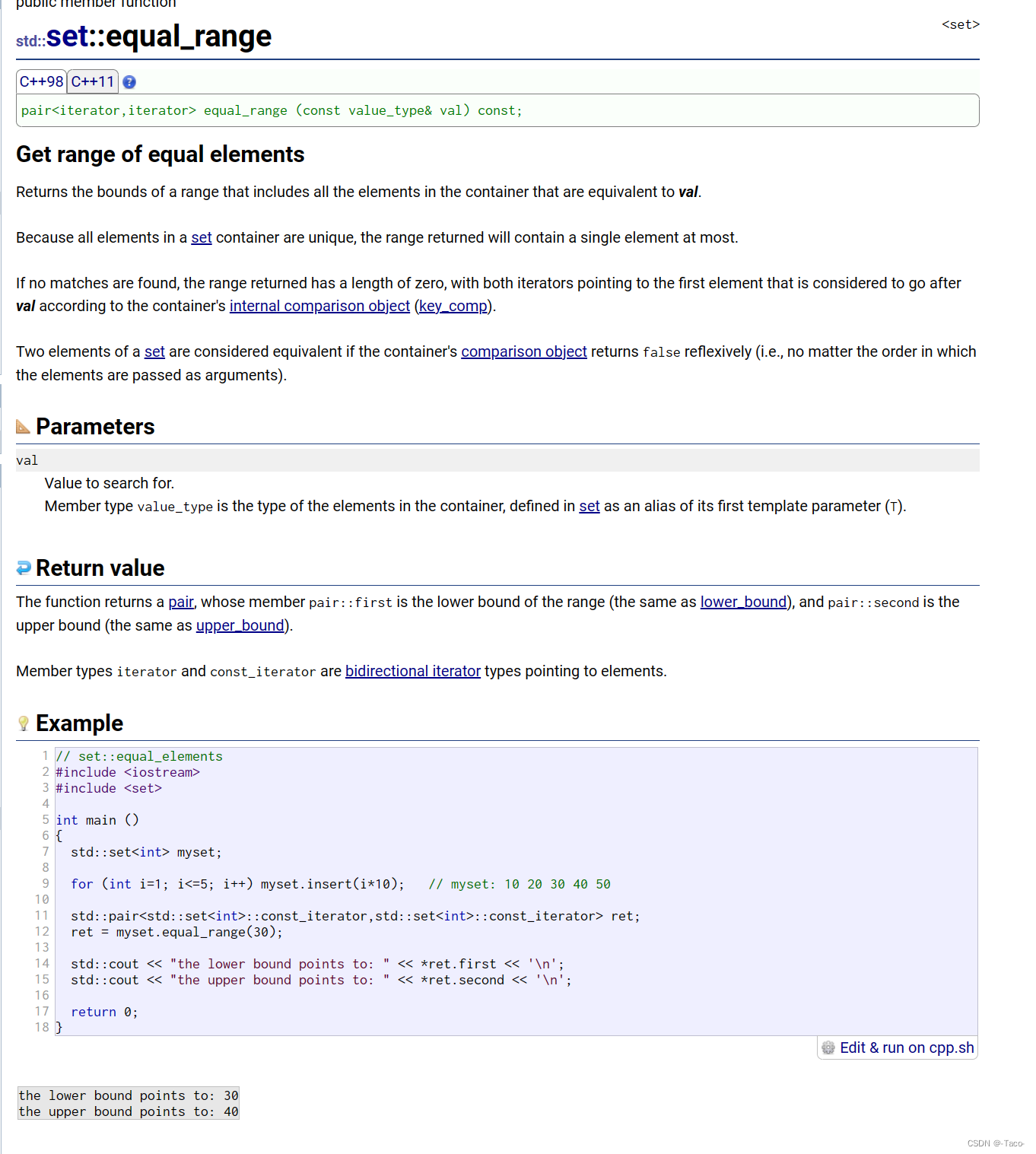
void test_set_07()
{
std::set<int> myset;
for (int i = 1; i <= 5; i++) myset.insert(i * 10); // myset: 10 20 30 40 50
std::pair<std::set<int>::const_iterator, std::set<int>::const_iterator> ret;
ret = myset.equal_range(35);// xx<=val<yy,找满足左闭右开的一组值
std::cout << "the lower bound points to: " << *ret.first << '\n';
std::cout << "the upper bound points to: " << *ret.second << '\n';
}
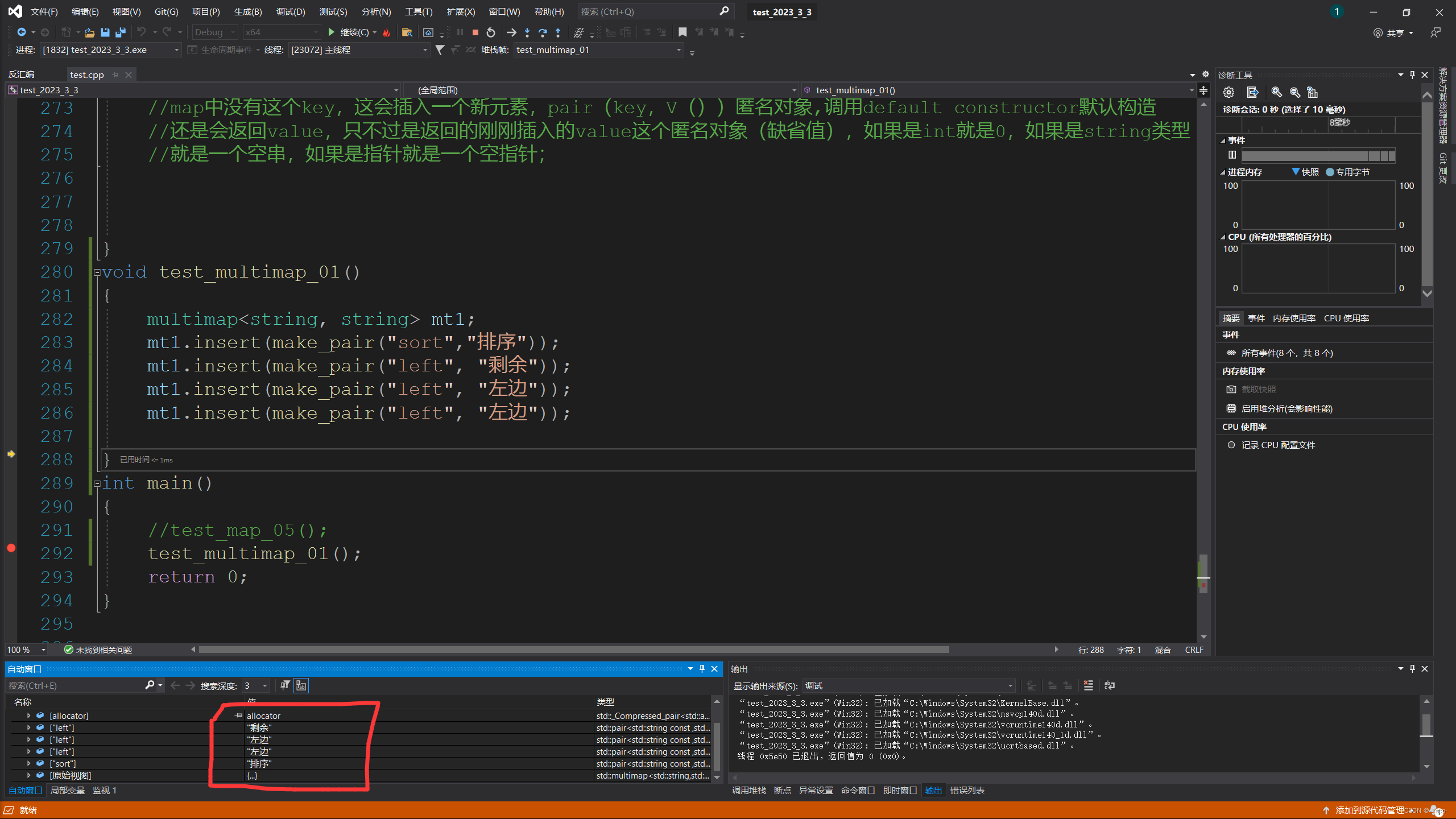
增删查没有改，搜索树是不允许修改；
如果直接定义好set的里面的值这时是const类型的，无法拷贝给正常定义的。
这里的pair是什么？
库里面给的一个函数，主要是给map用的
下来我们看multiset
它根set本质用法没有什么区别，唯一的区别就是允许建值冗余;
它的特点遍历的适合有序，这里的count还可以顺带查到值的个数，还有就是find 的区别，set的find 是有和无的区别，multiset的find如果有多个值是返回哪个？ --返回中序的第一个;这里如果调用erase是删所有的相同的值，要不逻辑会出现问题，给迭代器位置的话就指定这个位置的数；如果想删中序的下一个同样的数，++就可以，++之前是中序，之后会走下一个，++是函数调用；
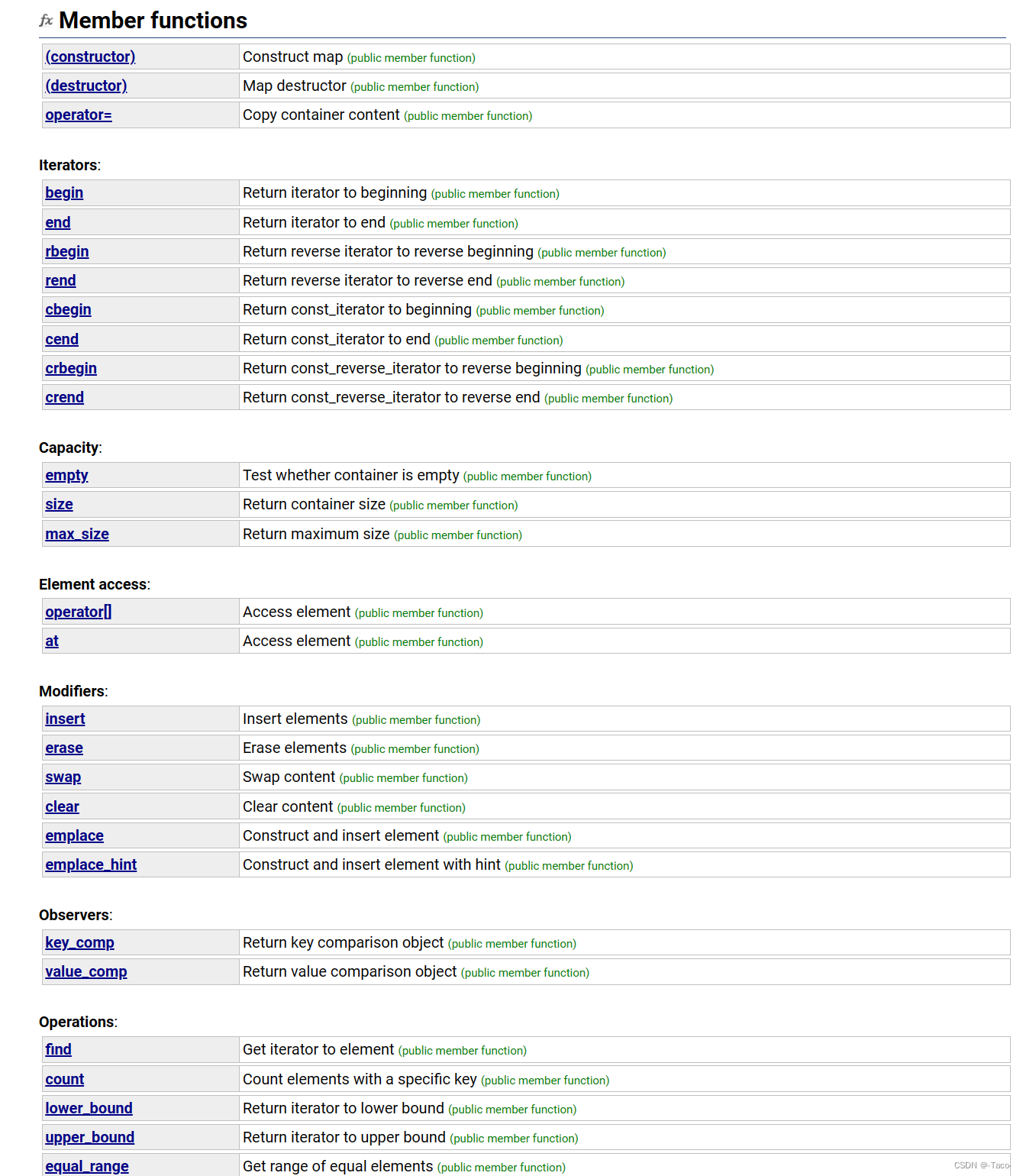
map
1. map是关联容器，它按照特定的次序(按照key来比较)存储由键值key和值value组合而成的元 素。
2. 在map中，键值key通常用于排序和惟一地标识元素，而值value中存储与此键值key关联的 内容。键值key和值value的类型可能不同，并且在map的内部，key与value通过成员类型 value_type绑定在一起，为其取别名称为pair: typedef pair value_type;
3. 在内部，map中的元素总是按照键值key进行比较排序的。
4. map中通过键值访问单个元素的速度通常比unordered_map容器慢，但map允许根据顺序 对元素进行直接迭代(即对map中的元素进行迭代时，可以得到一个有序的序列)。
5. map支持下标访问符，即在[]中放入key，就可以找到与key对应的value。
6. map通常被实现为二叉搜索树(更准确的说：平衡二叉搜索树(红黑树))。
key: 键值对中key的类型 T： 键值对中value的类型 Compare: 比较器的类型，map中的元素是按照key来比较的，缺省情况下按照小于来比 较，一般情况下(内置类型元素)该参数不需要传递，如果无法比较时(自定义类型)，需要用户 自己显式传递比较规则(一般情况下按照函数指针或者仿函数来传递) Alloc：通过空间配置器来申请底层空间，不需要用户传递，除非用户不想使用标准库提供的 空间配置器 注意：在使用map时，需要包含头文件。
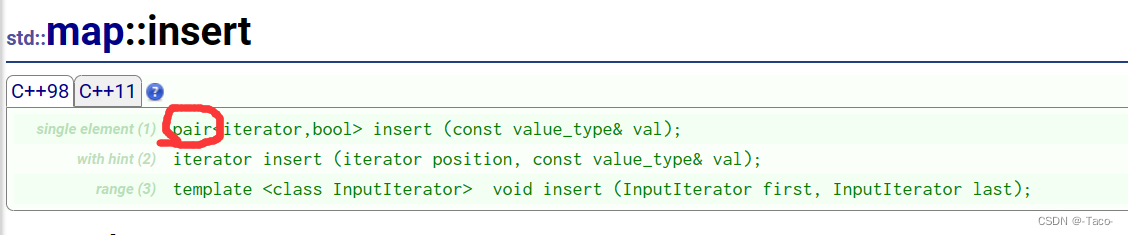
map在插入的时候是插入pair这个结构体；
template <class T1, class T2>
struct pair
{
typedef T1 first_type;
typedef T2 second_type;
T1 first;
T2 second;
pair(): first(T1()), second(T2())
{}
pair(const T1& a, const T2& b): first(a), second(b)
{}
};
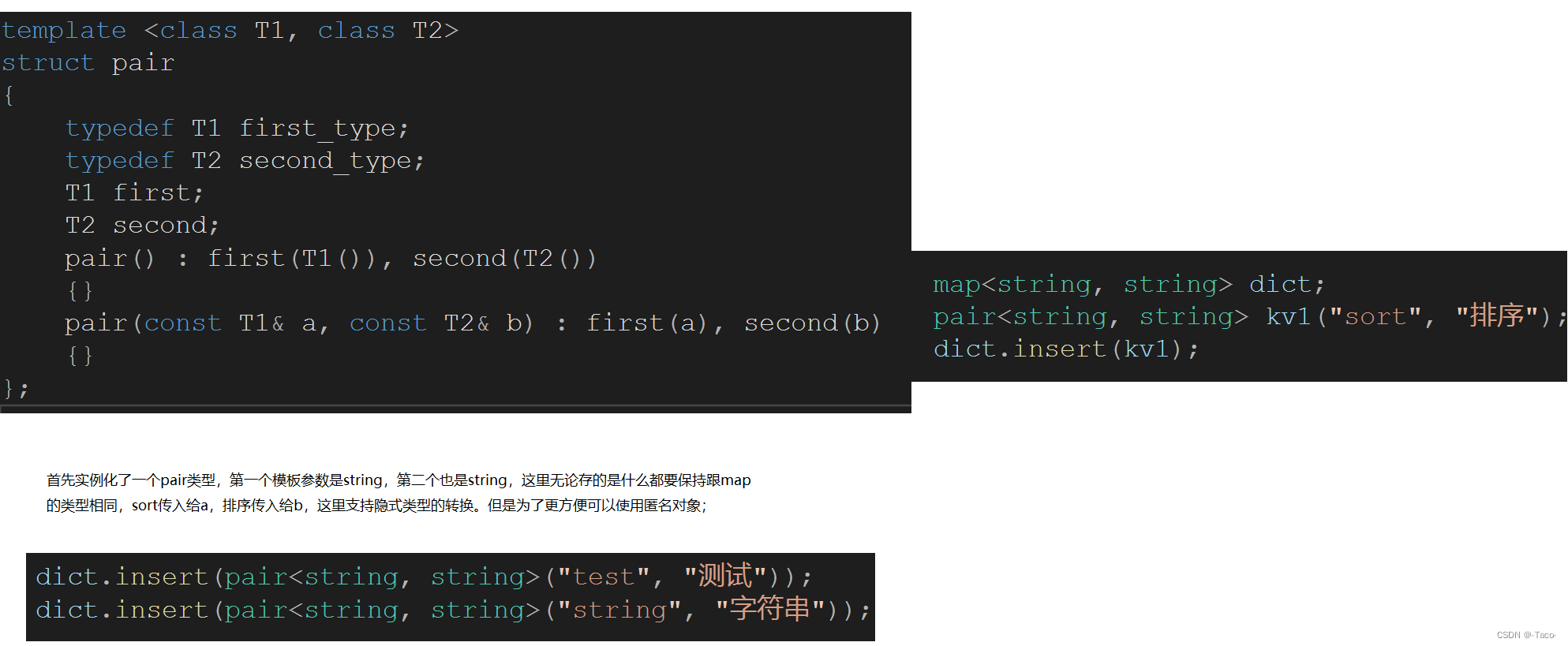
这里不能用auto，auto是左边推导右边，这里太复杂无法判断出auto，可以用typedef；
插入不能插相同的值，判断的时候是判断value值，
自动推导，不用显示的去写模板参数；这个make_pair的函数的时候会被写成inline；
写这map的时候不写pair的头文件也不会报错，因为pair的头文件被间接放在map里。
这里遍历的话，不能像之前一样遍历，因为key_value会返回两个值，c/c++没有函数可以接收返回两个值。 所以这里要用kv的键值对；
下面写统计次数的案例：
void test_map_03()
//统计次数
{
string arr[] = { "苹果","西瓜","苹果","西瓜","苹果","香蕉","苹果","香蕉","西瓜" };
map<string, int>countMap;
for (auto& str : arr)
{
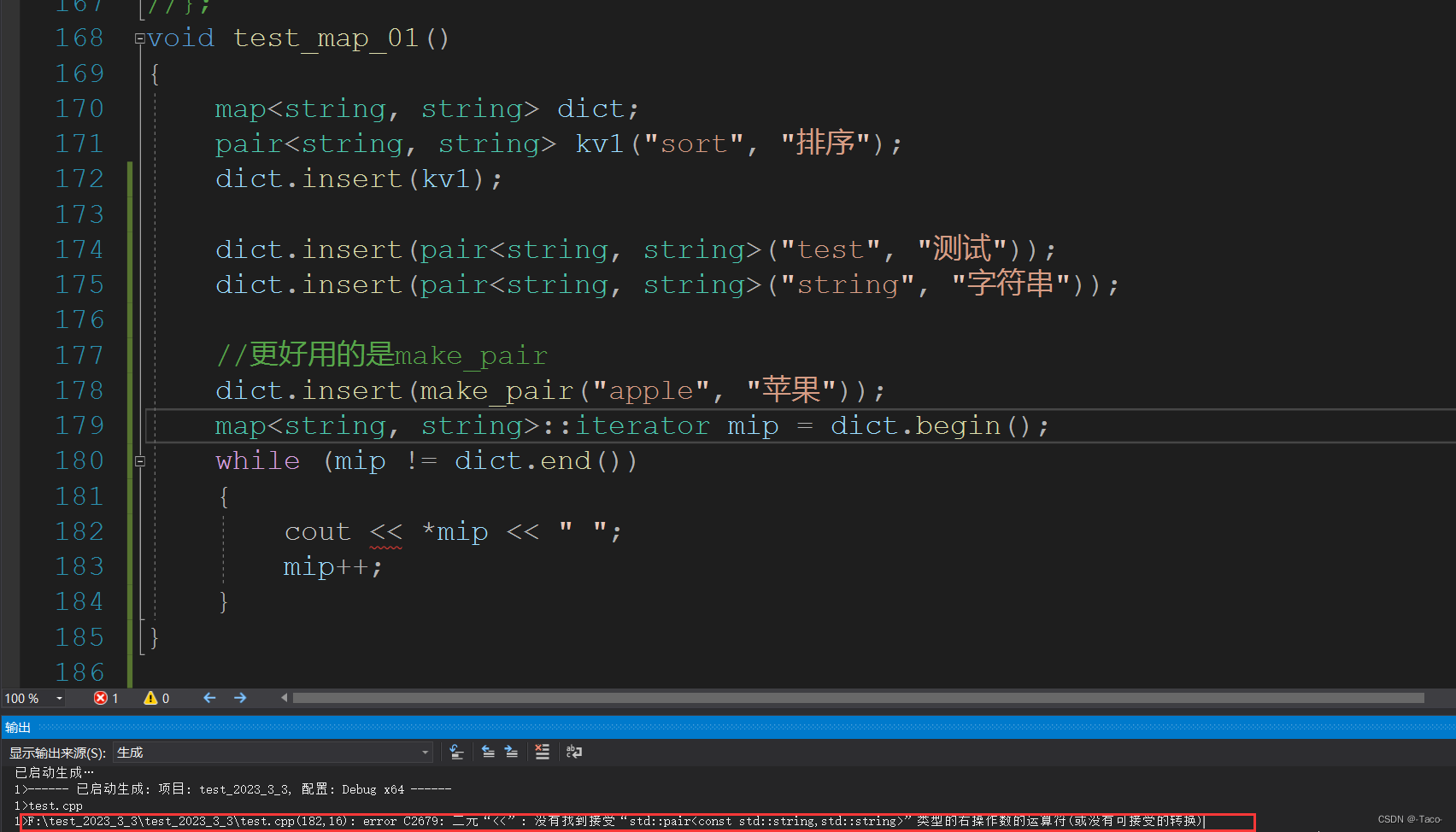
map<string, int>::iterator it = countMap.find(str);
if (it != countMap.end())
{
//1.(*it).second++;//想访问里面的数据，先调用operator*，解引用取出里面的数据，但是map里面的数据
//是一个结构，这个结构是pair，这里为什么不像我们之前自己写的搜索树里面存一个key和一个value呢？
//如果这样写，这里operator*无法同时返回两个值，还要修改，要返回两个值的引用，这里也不能临时
//组建一个结构体，因为临时对象不能使用引用返回；这里不习惯用这样的结构来调用
//迭代器是一个类指针的东西，有两种调用方式一种是.一种是->
//结构体指针就使用->,operator ->返回结构体里面数据的指针
//it->//返回的是pair*,之后要再加一个->，才能表示pair，但是为了美观，编译器优化，只需一个；
it->second++;
}
else
{
countMap.insert(make_pair(str, 1));
}
}
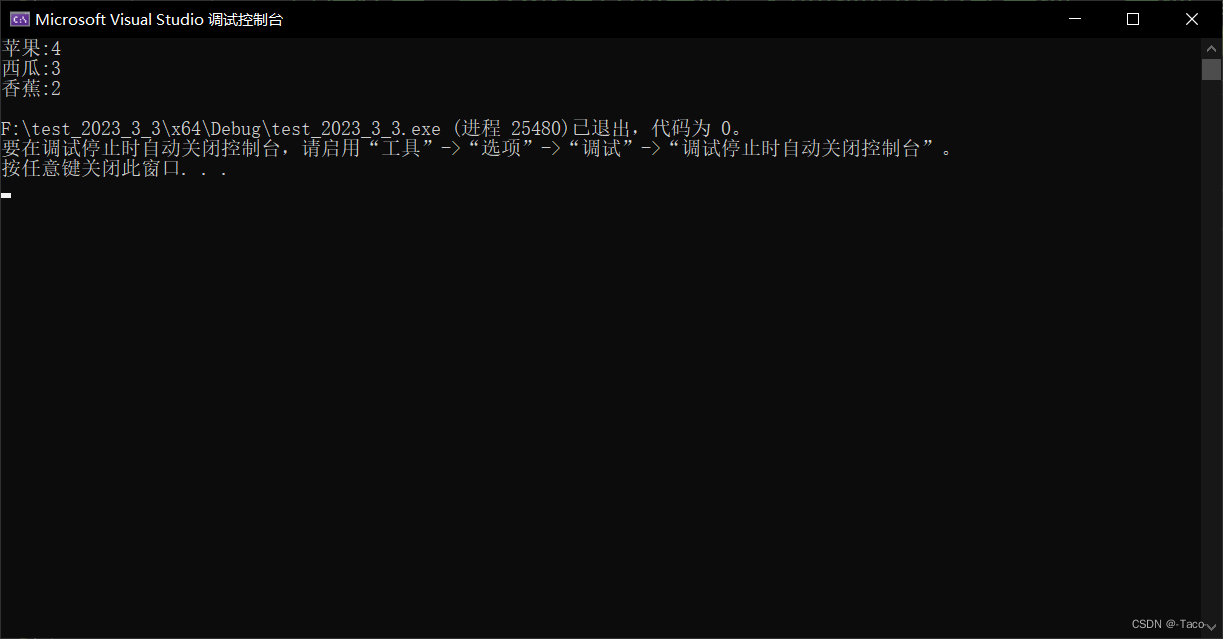
map<string, int>::iterator it = countMap.begin();
while (it != countMap.end())
{
cout << it->first << ":" << it->second << endl;
it++;
}
}
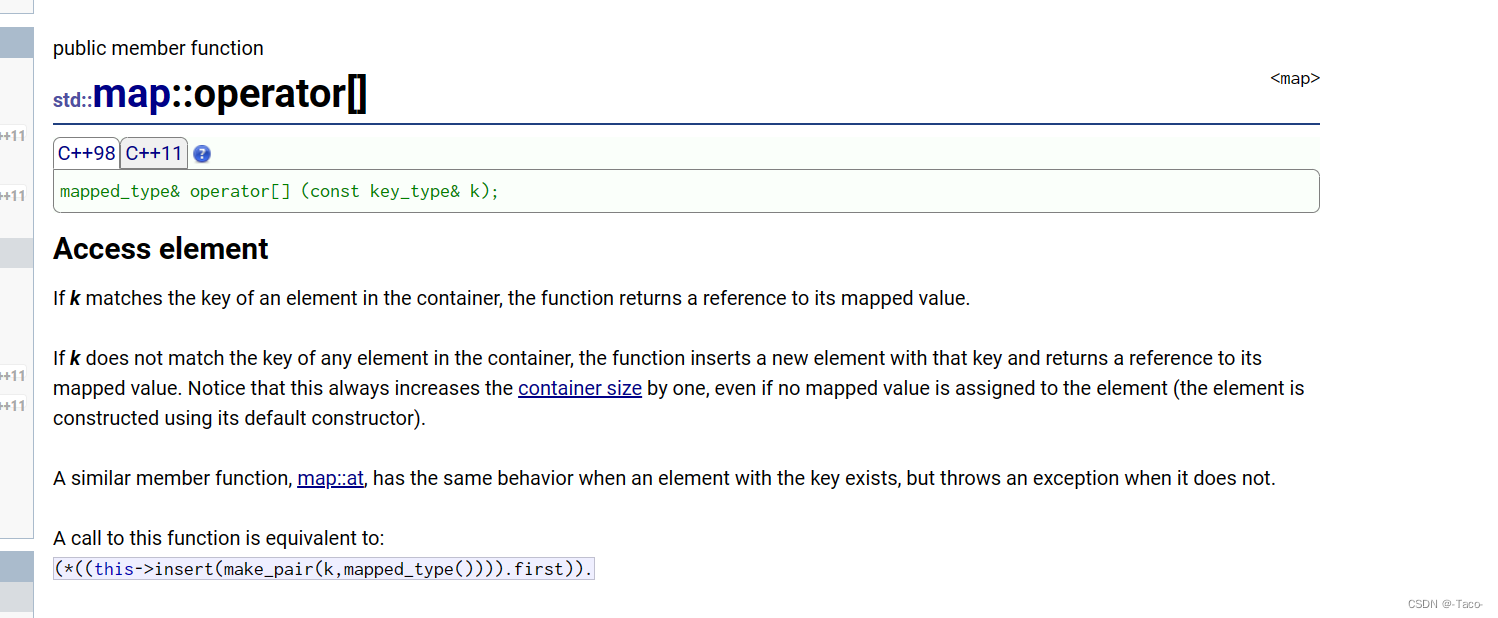
之前的[]是用于数组，下标访问，现在是树形结构，肯定不是下标访问，通过文档我们看出，是给一个key返回一个value是引用，对于统计次数，key是string，value是int，刚好我们可以加以利用；
void test_map_04()
{
map<string, int>countMap;
string arr[] = { "苹果","西瓜","苹果","西瓜","苹果","香蕉","苹果","香蕉","西瓜" };
//上面方法较复杂，更推荐[]
for (auto& e : arr)
{
countMap[e]++;
}
map<string, int>::iterator it = countMap.begin();
while (it != countMap.end())
{
cout << it->first << ":" << it->second << endl;
it++;
}
}
下面是对[]功能的详细解释；
这时候insert有就用insert后面的”插入“输入进去对应到insert；
这里完成了查找+修改的步骤；
[]插入属于插入+修改；功能非常的强大，at只是查找跟修改，如果在就返回一个引用，如果不在就抛出一个异常；
pair（str，int（））；int（）调用默认构造默认的值是0，再++就得到1；
str在countMap中，返回value的次数的引用，然后次数++； 在的话就是修改，不在的话就是插入+修改；
[]的实现：
这里调用的太过复杂，我们先来看insert
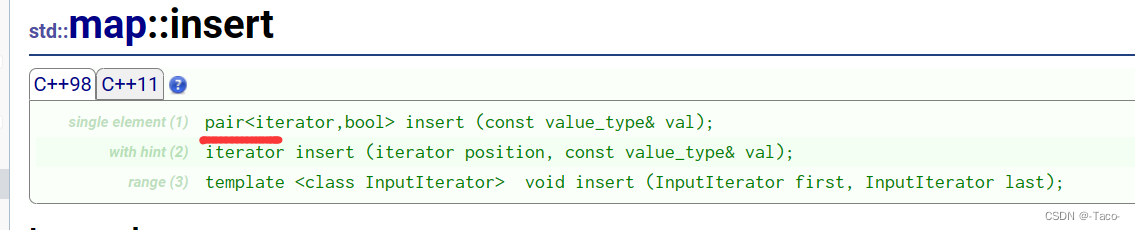
返回的是一个pair
上面的value_type 是一个pair，pair<K<V>插入的时候只看k
如果key已经在map中返回pair<key_iterator,false>;如果key存在返回key所在的迭代器，这里存false；
如果key不在map中返回pair<new_key_iterator,true>返回新插入的元素的迭代器；
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
//key两种可能性，一种是key不在，插入成功，返回value的引用，迭代器是新插入的元素的迭代器
//key在的话，插入失败，返回的是已经存在的元素的迭代器
//迭代器插入成功还是失败都是返回的是这个key所在的，如果是已经有了这里V（）的缺省值就没起任何作用；
return ret.first->second;
//返回key所对的这个value
//ret.first就是这个迭代器，迭代器->就是pair*，再加->就是取pair的first和second了
}
这样就把return（*（（this->insert(make_pair(k,mapped_tyoe()))).first)）.second;给拆散成上面两步；insert的返回值就是pair，调用了pair的first就是迭代器，之后迭代器就代表无论是新插入的还是旧的，之后迭代器解引用得到pair，再取pair的second；
有两个pair，一个是insert的pair，一个是迭代器的pair
insert的返回是pair的意义就在此，[] 的实现，如果没有pair就得find 再找一边，就得走两次树；
multimap
跟multiset一样，允许建值的冗余，就没有[] 的功能了，multimap就不能帮我们统计次数了；
1. Multimaps
是关联式容器，它按照特定的顺序，存储由
key
和
value
映射成的键值对
<key,
value>
，其中多个键值对之间的
key
是可以重复的。
2.
在
multimap
中，通常按照
key
排序和惟一地标识元素，而映射的
value
存储与
key
关联的内
容。
key
和
value
的类型可能不同，通过
multimap
内部的成员类型
value_type
组合在一起，
value_type
是组合
key
和
value
的键值对
:
typedef pair<const Key, T> value_type
;
3.
在内部，
multimap
中的元素总是通过其内部比较对象，按照指定的特定严格弱排序标准对
key
进行排序的。
4. multimap
通过
key
访问单个元素的速度通常比
unordered_multimap
容器慢，但是使用迭代
器直接遍历
multimap
中的元素可以得到关于
key
有序的序列。
5. multimap
在底层用二叉搜索树
(
红黑树
)
来实现。
注意：
multimap
和
map
的唯一不同就是：
map
中的
key
是唯一的，而
multimap
中
key
是可以
重复的
。
3.4.2 multimap
的使用
multimap
中的接口可以参考
map
，功能都是类似的。
注意：
multimap
中的
key
是可以重复的。
multimap
中的元素默认将
key
按照小于来比较
使用时与map
包含的头文件相同：
mutimap的简单应用：
下面是综合应用：
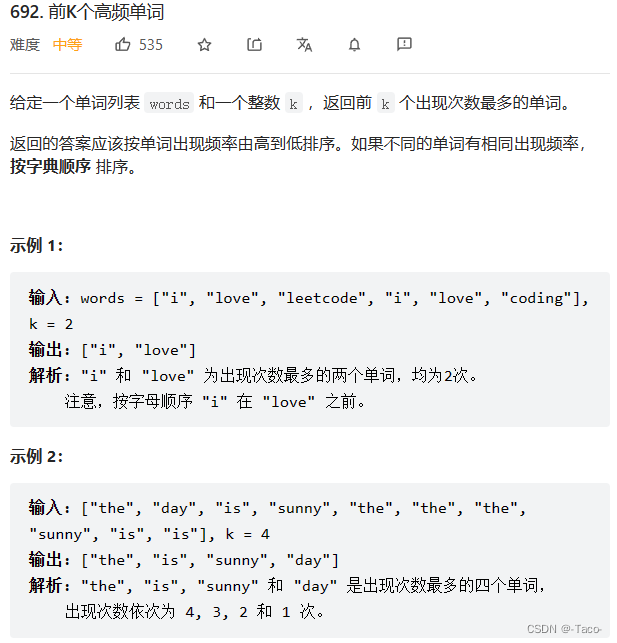
class Solution {
public:
vector<string> topKFrequent(vector<string>& words, int k) {
map<string,int>countMap;
for(auto&str:words)
{
//[]返回是value的引用，value是int，整体++用来计数
countMap[str]++;
}
//对计数完之后的进行排序（不能去重，防止次数一致的被去除掉）
//需要用greater，不能用反向迭代器去取
//如果出现类似 i：2，l：2次，如果按反向迭代器去
//遍历的话是 l：2，i：2，但是次数相同要按照字典
//顺序，应该是i在前，所以不能用反向迭代器，用仿函数
multimap<int,string,greater<int>> SortMap;
for(auto&kv:countMap)
{
SortMap.insert(make_pair(kv.second,kv.first));
}
vector<string>v;
multimap<int,string>::iterator it=SortMap.begin();
for(size_t i=0;i<k;i++)
{
v.push_back(it->second);
it++;
}
return v;
}
};
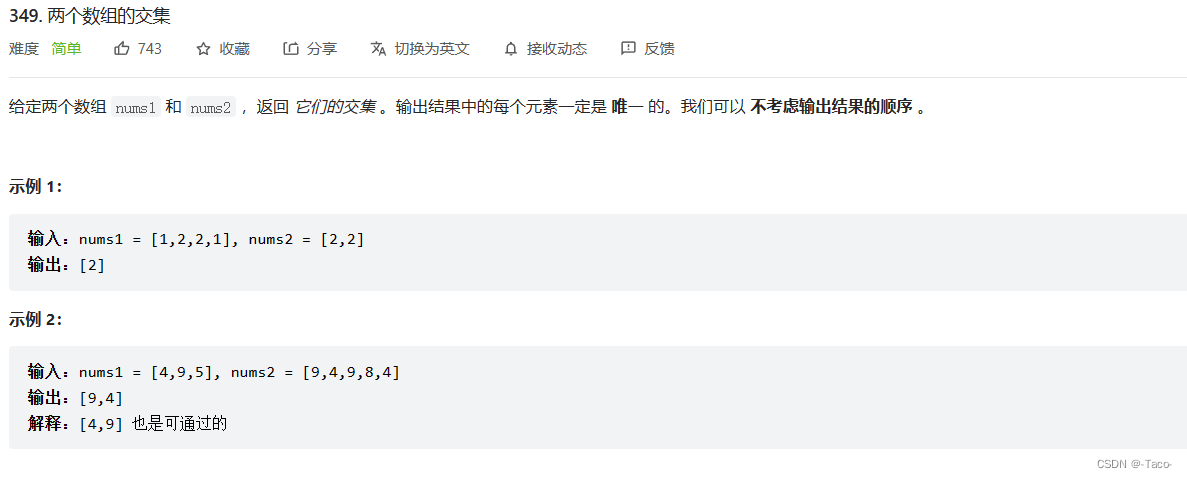
思路1双循环加vector的迭代器构造法；
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
set<int> s1;
for (size_t i = 0; i < nums1.size(); i++)
{
for (size_t j = 0; j < nums2.size(); j++)
{
if (nums1[i] == nums2[j])
{
s1.insert(nums1[i]);
}
}
}
vector<int>v1(s1.begin(), s1.end());
return v1;
}
};思路2：先有序，最后走双指针，开头更小的序列先走，如果两个数相等就是交集，同时++；
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
// 先去重
set<int> s1;
for(auto e : nums1)
{
s1.insert(e);
}
set<int> s2;
for(auto e : nums2)
{
s2.insert(e);
}
// set排过序，依次比较，小的一定不是交集，相等的是交集
auto it1 = s1.begin();
auto it2 = s2.begin();
vector<int> ret;
while(it1 != s1.end() && it2 != s2.end())
{
if(*it1 < *it2)
{
it1++;
}
else if(*it2 < *it1)
{
it2++;
}
else
{
ret.push_back(*it1);
it1++;
it2++;
}
}
return ret;
}
};
4.
底层结构
前面对
map/multimap/set/multiset
进行了简单的介绍，在其文档介绍中发现，这几个容器有个
共同点是：
其底层都是按照二叉搜索树来实现的
，但是二叉搜索树有其自身的缺陷，假如往树中
插入的元素有序或者接近有序，二叉搜索树就会退化成单支树，时间复杂度会退化成
O(N)
，因此
map
、
set
等关联式容器的底层结构是对二叉树进行了平衡处理，即采用平衡树来实现。
AVL 树 ---
也叫高度平衡二叉搜索树；
map和set最终用的是红黑树，这里avl树只是一个过渡；
AVL
树的概念
二叉搜索树虽可以缩短查找的效率，但
如果数据有序或接近有序二叉搜索树将退化为单支树，查
找元素相当于在顺序表中搜索元素，效率低下
。因此，两位俄罗斯的数学家
G.M.Adelson-Velskii
和
E.M.Landis
在
1962
年
发明了一种解决上述问题的方法：
当向二叉搜索树中插入新结点后，如果能保证每个结点的左右
子树高度之差的绝对值不超过
1(
需要对树中的结点进行调整
)
，即可降低树的高度，从而减少平均
搜索长度。
一棵
AVL
树或者是空树，或者是具有以下性质的二叉搜索树：
它的左右子树都是
AVL
树
左右子树高度之差
(
简称平衡因子
)
的绝对值不超过
1(-1/0/1）
（非必须）
平衡因子：右子树的高度-左子树的高度；
非必须的意思是也可以不要，我们这么用是为了方便实现；
为什么要保证左右高度差不超过1，为什么不是0？
因为树形结构的节点插入之后一个可以做到为0，但是两个节点插入进去之后无法保证高度差为0，两个节点必定有高低之分，所以确保不超过1即可，做不到为0；
所以这颗树任意一个子树它的左右高度差都不超过1
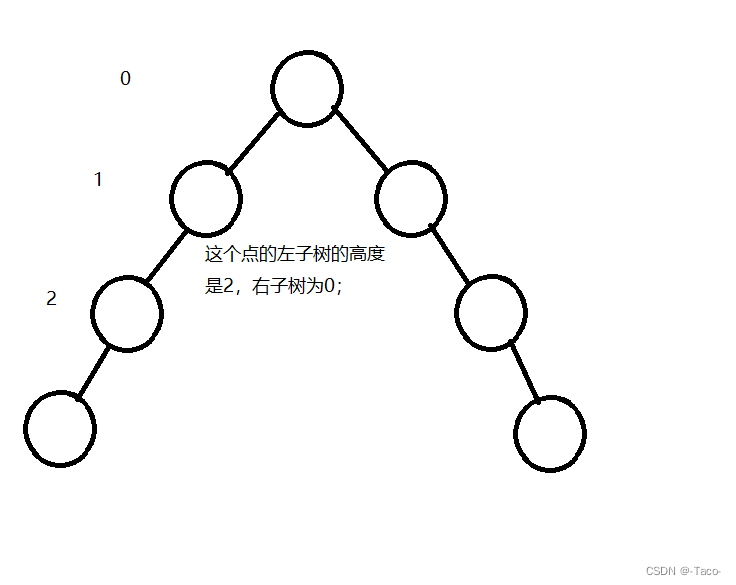
这种结构就不是AVL树；
最后一定是类似完全二叉树了，高度基本控制在logN，最后一层或者两层可能不满，
增删查改的效率及其高
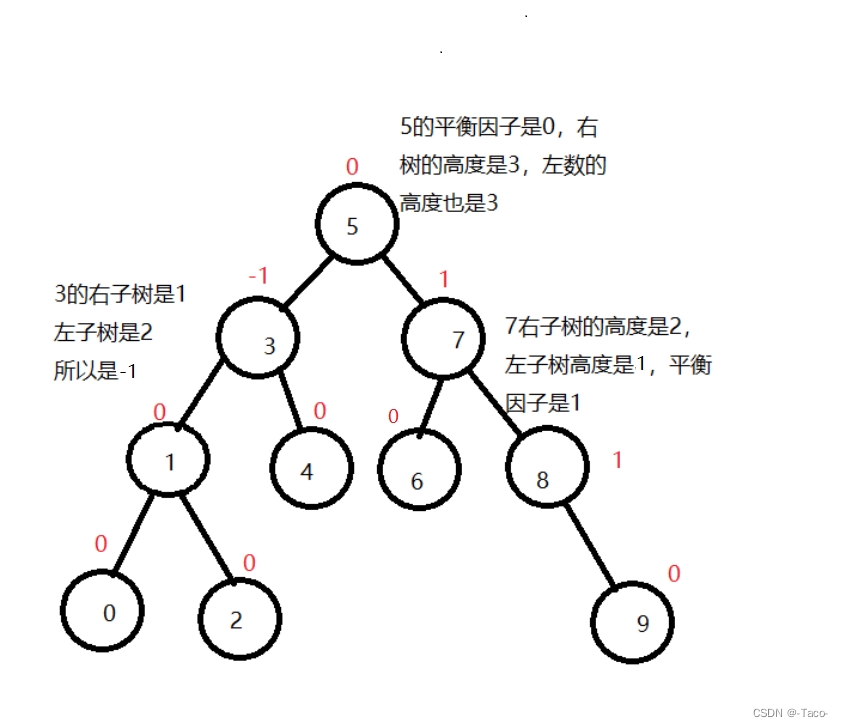
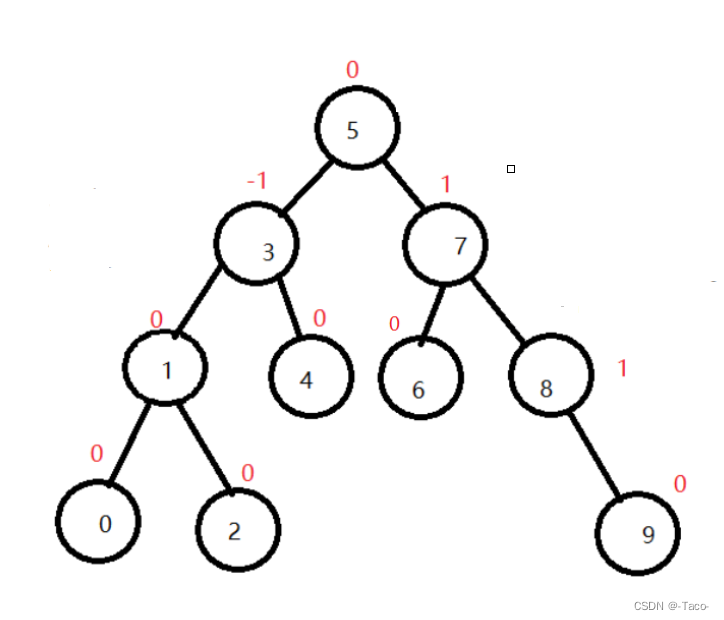
有平衡因子就是有一个量化的值，平衡因子对树就是对的，出问题的话就得做旋转，平衡因子是方便我们去实现树；
哈夫曼树在实际中没有很大的应用价值，它严格来说不是一个存储型的数据结构，哈夫曼树是功能性树，可以用于哈夫曼编码，用作文件压缩；
平衡因子是子树的高度差，插入节点是影响上面的祖先，要去更新它的祖先路径，
先来介绍一下三叉链表
在二叉链表的存储方式下，从某结点出发可以直接访问到它的孩子结点，但要找到某个结点的父节点需要从根节点开始搜索，最坏情况下，需要遍历整个二叉链表。
而三叉链表，在二叉链表的基础上加了一个指向父结点的指针域，使得即便于查找孩子结点，又便于查找父结点，但相对二叉链表而言，加大了空间开销。
首先先构建一个node的节点：
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
pair<K, V>_kv;
int _bf;//balance factor:平衡因子(设计时非必须）
};
之后像我们之前写搜索二叉树一样的步骤，使用非递归的方式写入节点的插入：
template<class K,class V>
struct AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
//先插入之后再平衡
//写的时候能用非递归就尽量用非递归；
bool Insert(const pair<K,V>&kv)//插入的时候本质上还是跟搜索树是一样的；(大就往右走，小就往左走）
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)//让cur走到空的位置，parent指向cur
{
if (cur->_kv.first < kv.first)//插入的值比这个大走右边
{
parent = cur;
cur = cur->_right;
}
else if(cur->_kv.first>kv.first)//插入的值比要比较的值小，就走左边
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//这里就该插入了：
cur = new Node(kv);
if (parent->_kv.first < kv.first)//插入的值比这个值要大就链接在右边
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//parent是怎么连接的，插入第一个节点不需要考虑parent；
cur->_parent = parent;//三叉链
return true;
}
private:
Node* _root;
};
这里只是多了一步：用cur的parent去链接它的parent，达到三叉链的效果，为了后面引入平衡因子
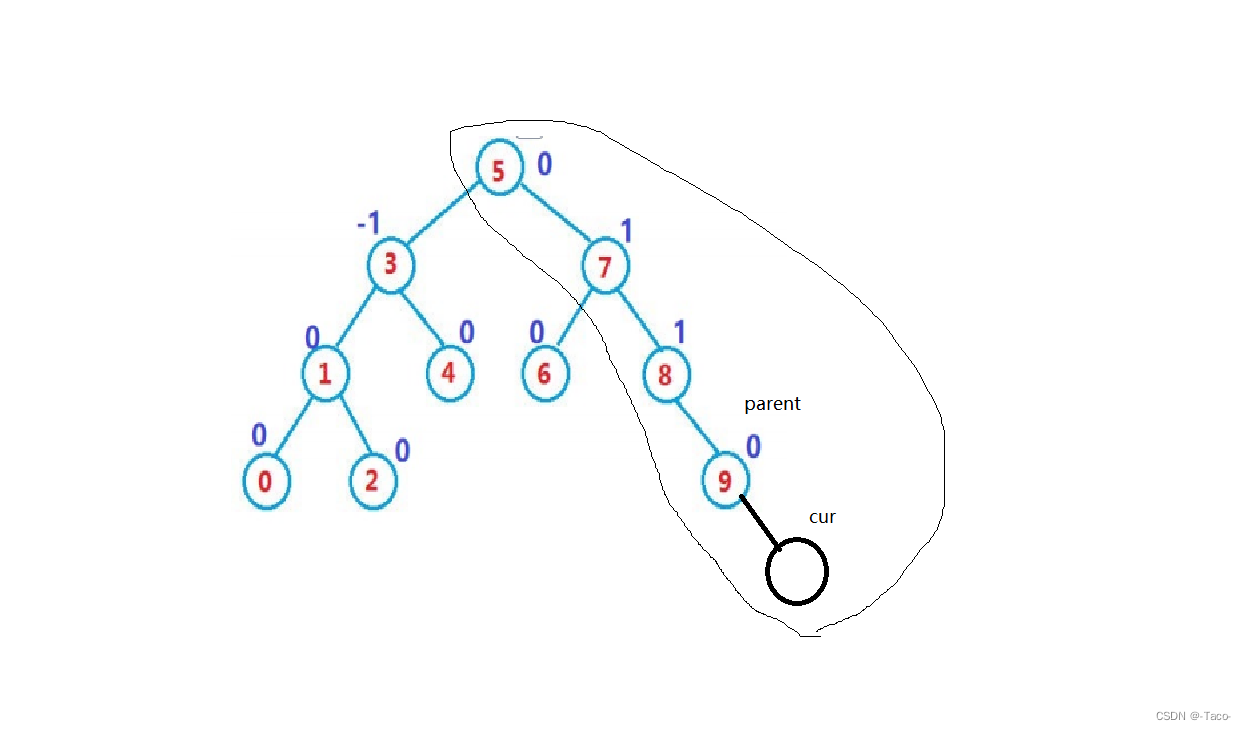
node插入这里，不会影响左树，至多影响画出来的，也就是它的祖先；
沿着自己的三叉链一路往上更新，也不需要更新到root，分情况讨论：
插入一个节点平衡因子一定为0；
怎么更新？
->如果新插入的cur是parent的右边，cur的parent的平衡因子要怎么更新？
新增是让高度+1，它的parent+1，在左边这个parent-1；
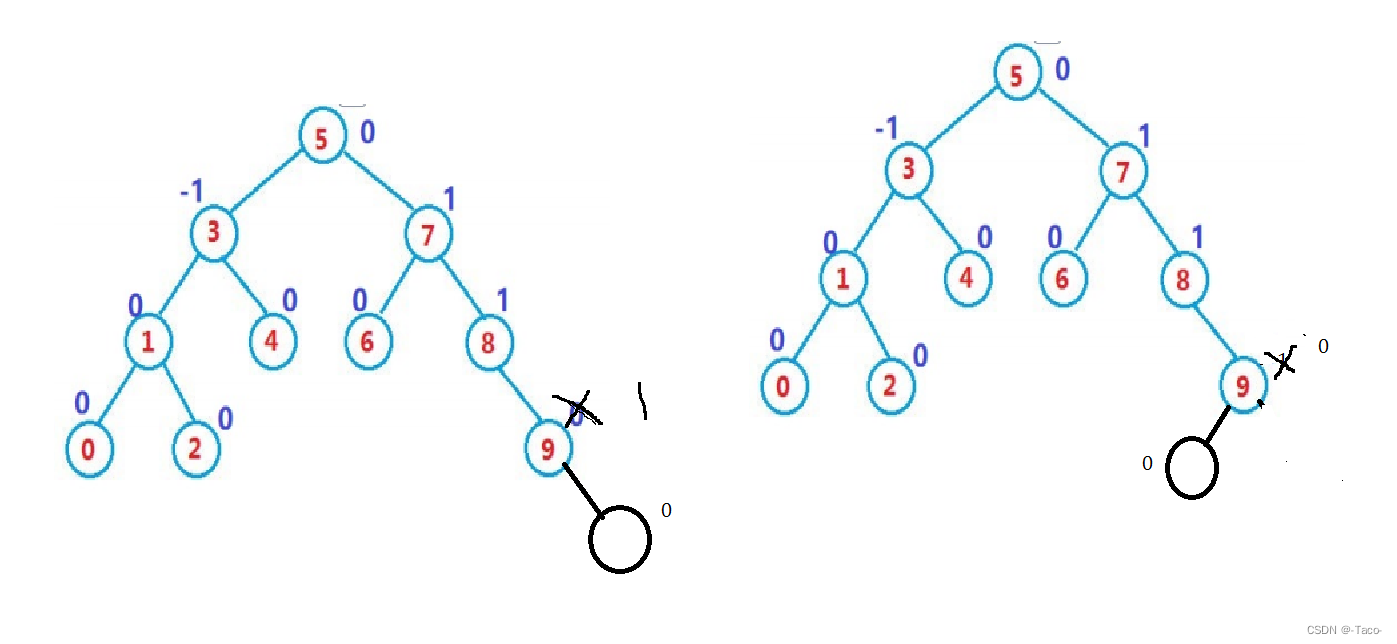
更新平衡因子的规则：（平衡因子就是左右子树一样高就是0，左高右低为-1，左低右高为+1)
1.新增在右边，parent的平衡因子++，新增在左，parent的平衡因子--；
2.更新后parent的平衡因子等于1或者-1，（1代表右边高，-1代表左边高）如果变了继续更新即可，如果高度没有变化就不继续更新，变成1/-1，证明了parent插入前的平衡因子肯定是0；说明左右子树高度相等，现在变成有-1左边高，1右边高这种情况，parent的高度变了，需要继续往上更新，因为它对上一层有影响；
3.如果更新后平衡因子是0，就不用往上更新了，说明更新之前是-1/1，说明左右子树一边高一边低，说明插入填入了矮的那一边，插入之后两边一样高，parent所在的子树高度不变；
4.如果更新之后平衡因子是-2或者2，证明之前是1、-1，已经是平和的临界值（有一边已经高了），说明已经打破平衡，parent所在的子树，需要旋转处理；
5.更新后parent会不会变成大于2或小于-2的值，如果存在，只能说明插入前不是AVL树，需要检查之前的插入过程；
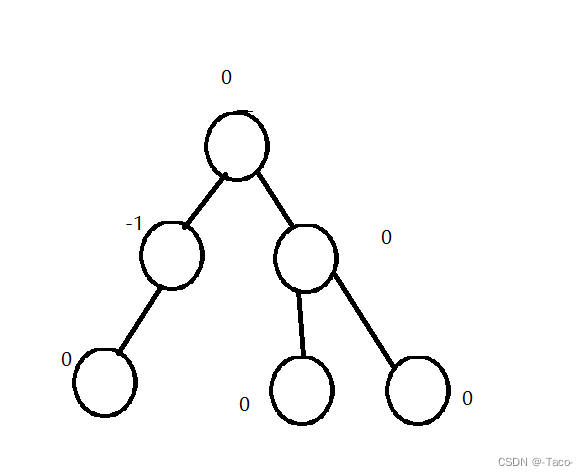
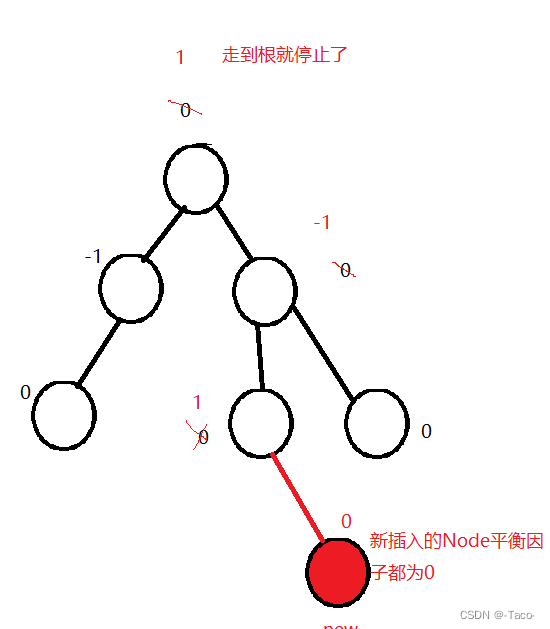
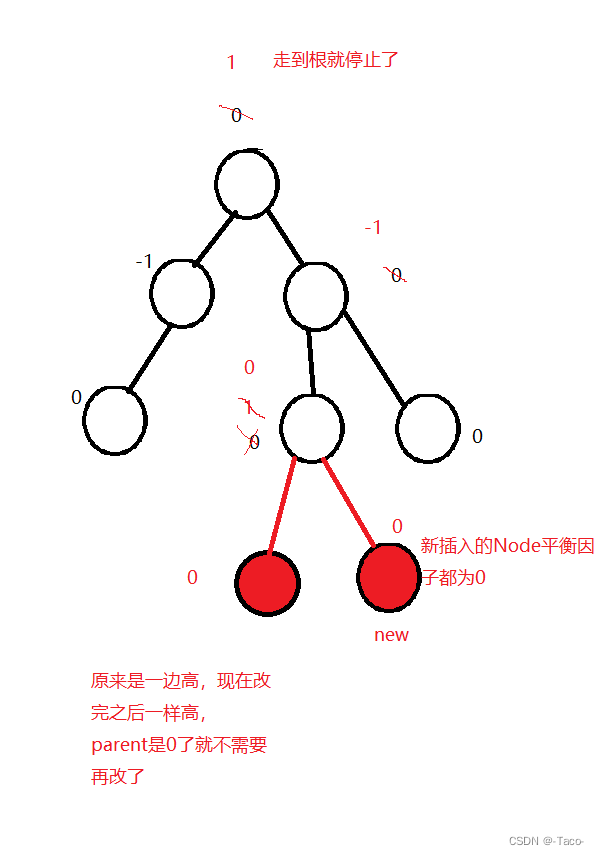
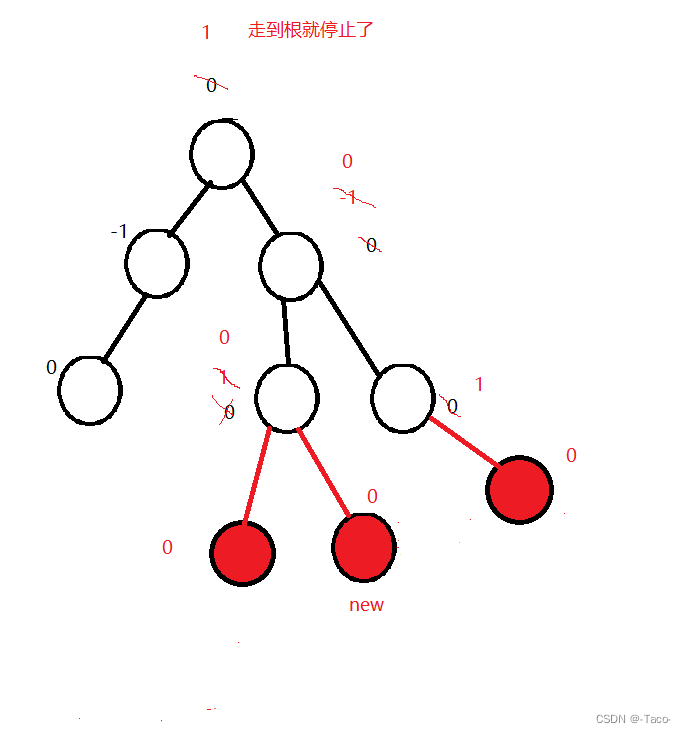
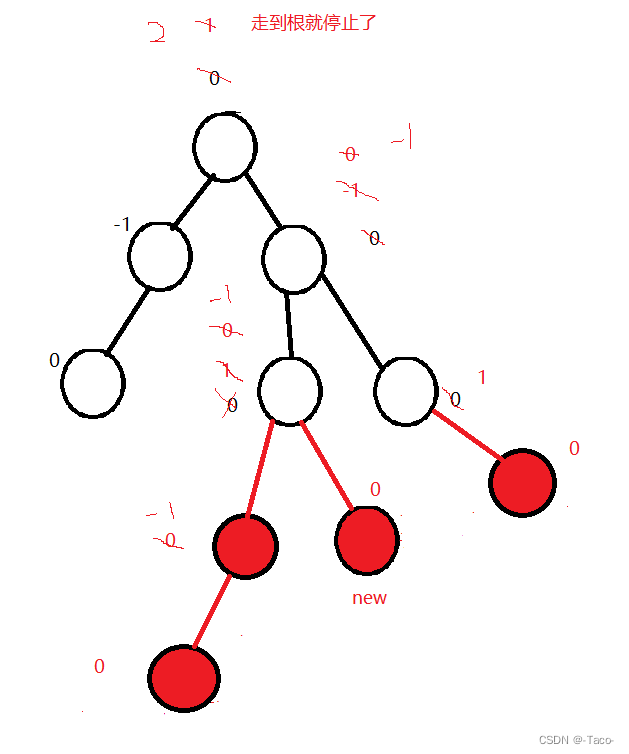
将我们上述图的规则用代码实现出来：
//控制平衡（有可能插入的时候已经平衡了，有可能也没平衡）
//新插入节点的平衡因子肯定是0，之后沿着这个节点往上去更新平衡因子;
//1.更新平衡因子
while (parent != nullptr)//最坏的情况有可能更新到根节点；（只有根节点的父亲为null）
{
if (cur == parent->_right)
{
parent->_bf++;
}
else
{
parent->_bf--;
}
if (parent->_bf == 0)
{
break;
}
else if (parent->_bf == -1 || parent->_bf == 1)
{
//继续更新，三叉链；
parent = parent->_parent;
cur = cur->_parent;
}
else if (abs(parent->_bf == 2))//绝对值，求出来bf为±2；
{
//说明parent所在的子树已经不平衡了，需要旋转处理；
}
else
{
//parent是大于2的，说明插入之前是出现问题的，
assert(false);//报错；
}
}这会儿右边的高度是4，左边的是2，已经失衡了，就需要旋转；
AVL
树的旋转（前提的到2，才会需要旋转）
处理的原则：
1.旋转成平衡树 2.保持搜索树规则
共性：出问题的都是parent
右边高，可以想办法让它朝左边走；
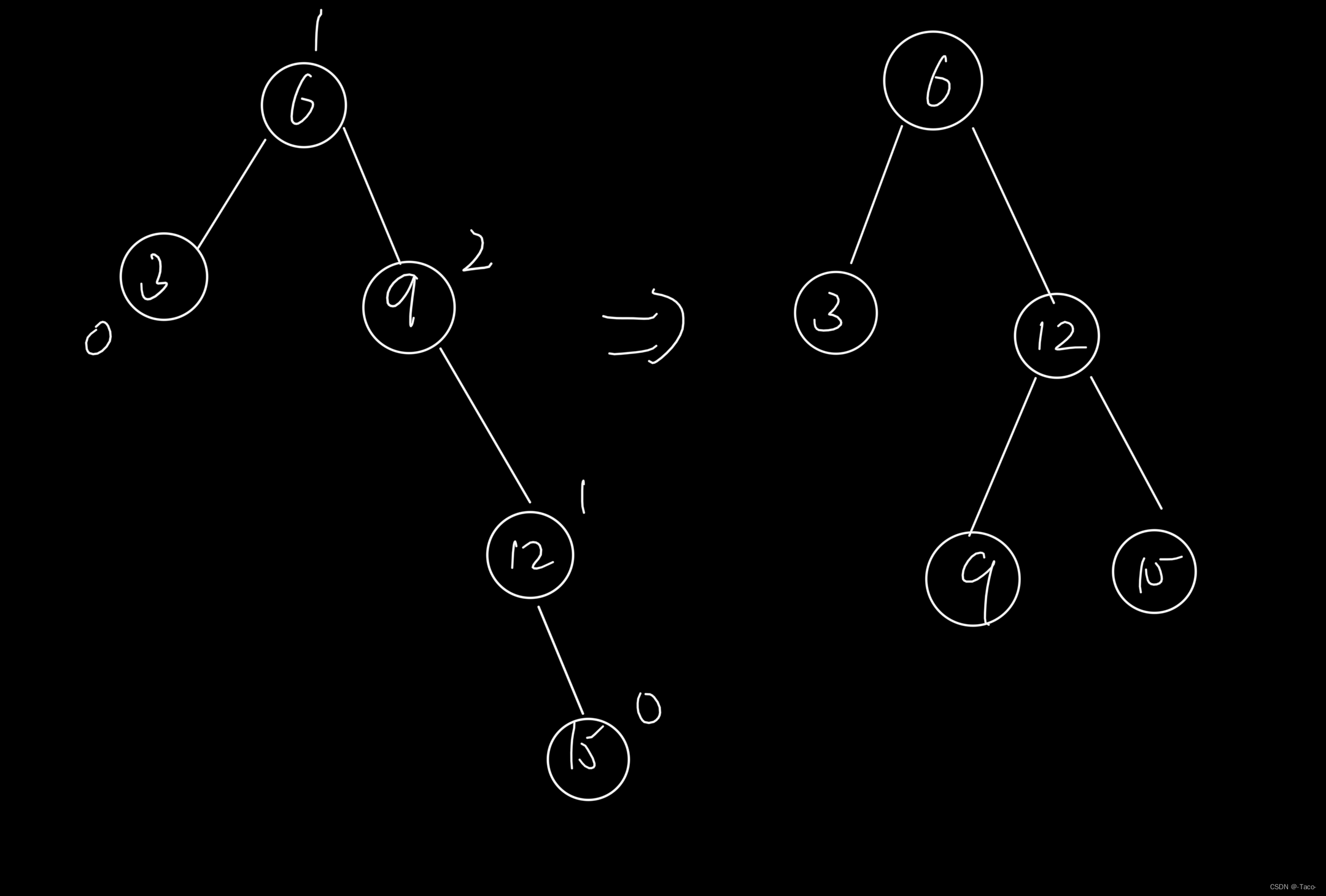
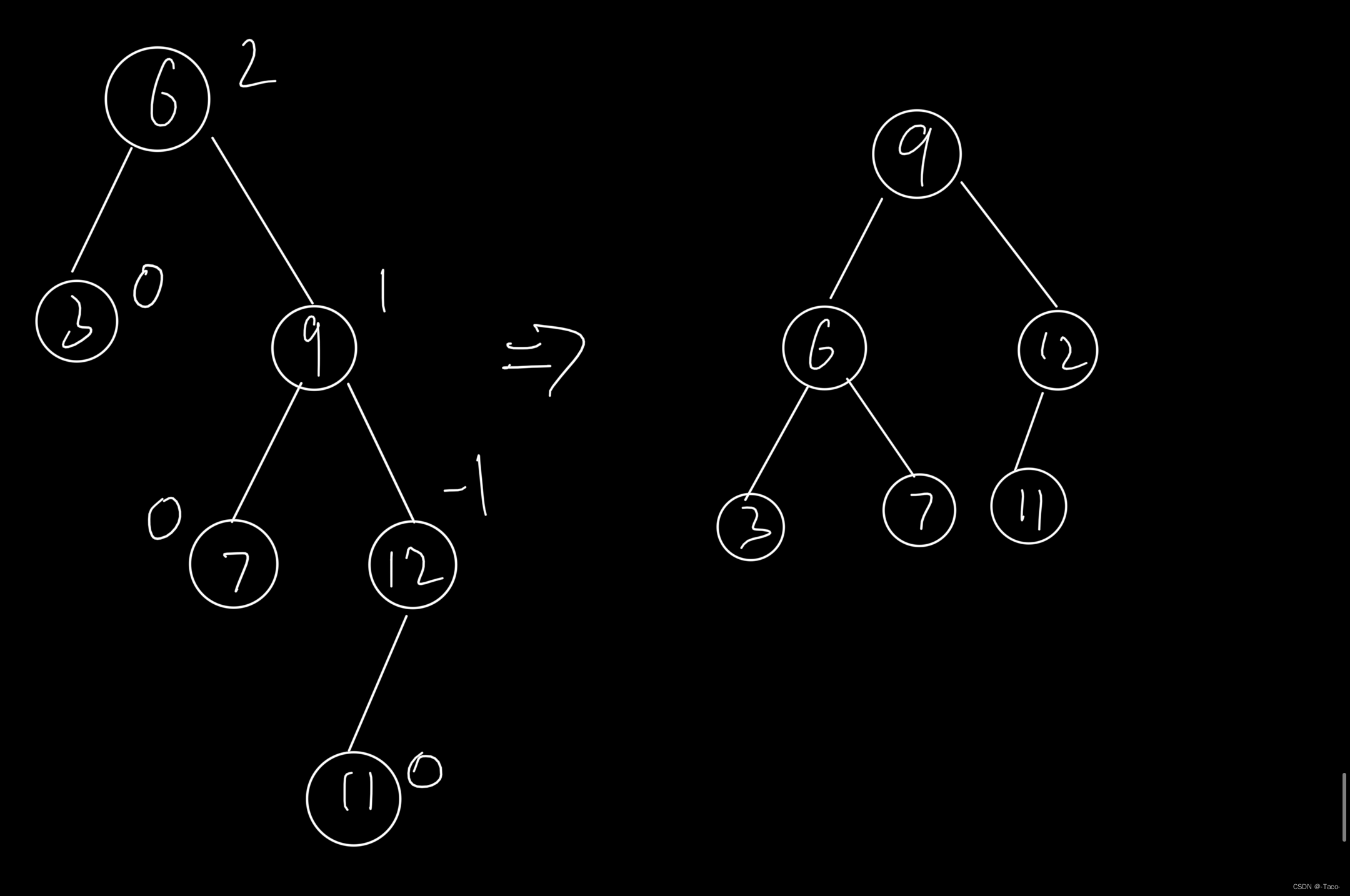
面对这些情况，有归类去解决；
如果在一棵原本是平衡的
AVL
树中插入一个新节点，可能造成不平衡，此时必须调整树的结构，
使之平衡化。根据节点插入位置的不同，
AVL
树的旋转分为四种：
1.
新节点插入较高右子树的右侧
---
右右：左单旋
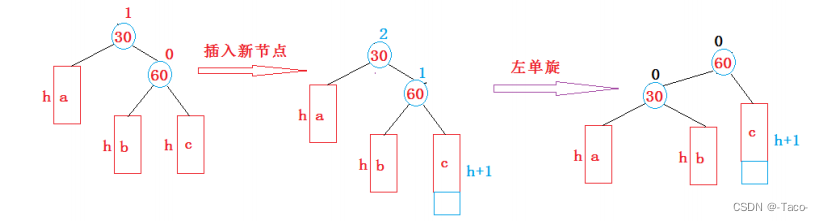
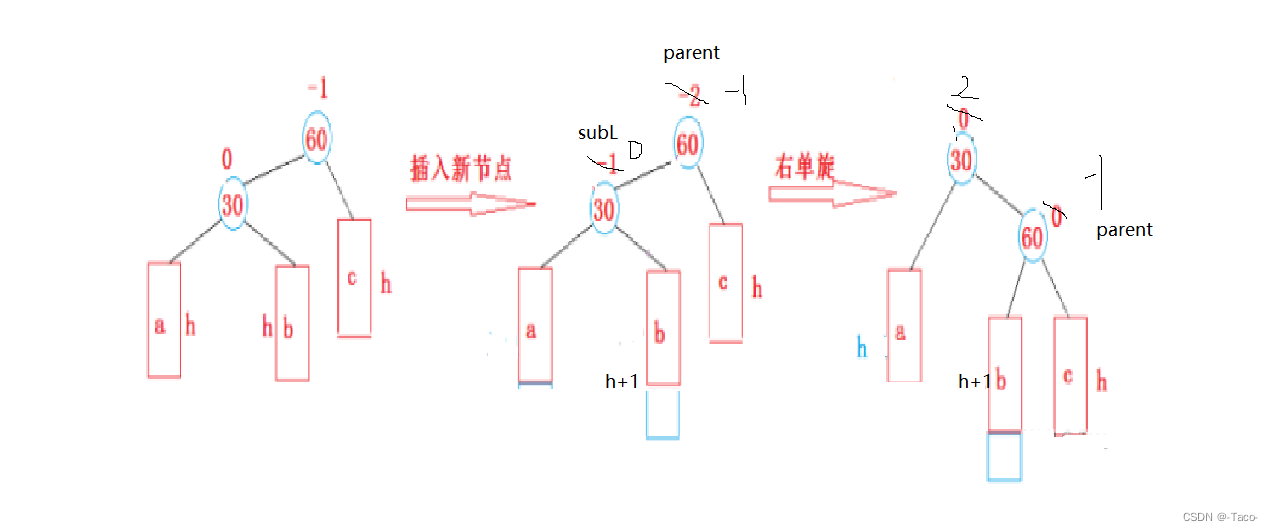
c从h变成h+1，60的平衡因子就变成1了，继续更新，30就变成2，当30==2的时候就说明需要旋转了，右边高，这时候30右边的高度就变成h+2；左旋转，把30压下去，做60的左边，60的左边有b，当60的左b做30的右；这时候就达到平衡了；60就变成了根；
具象图：
代表很多种情况：
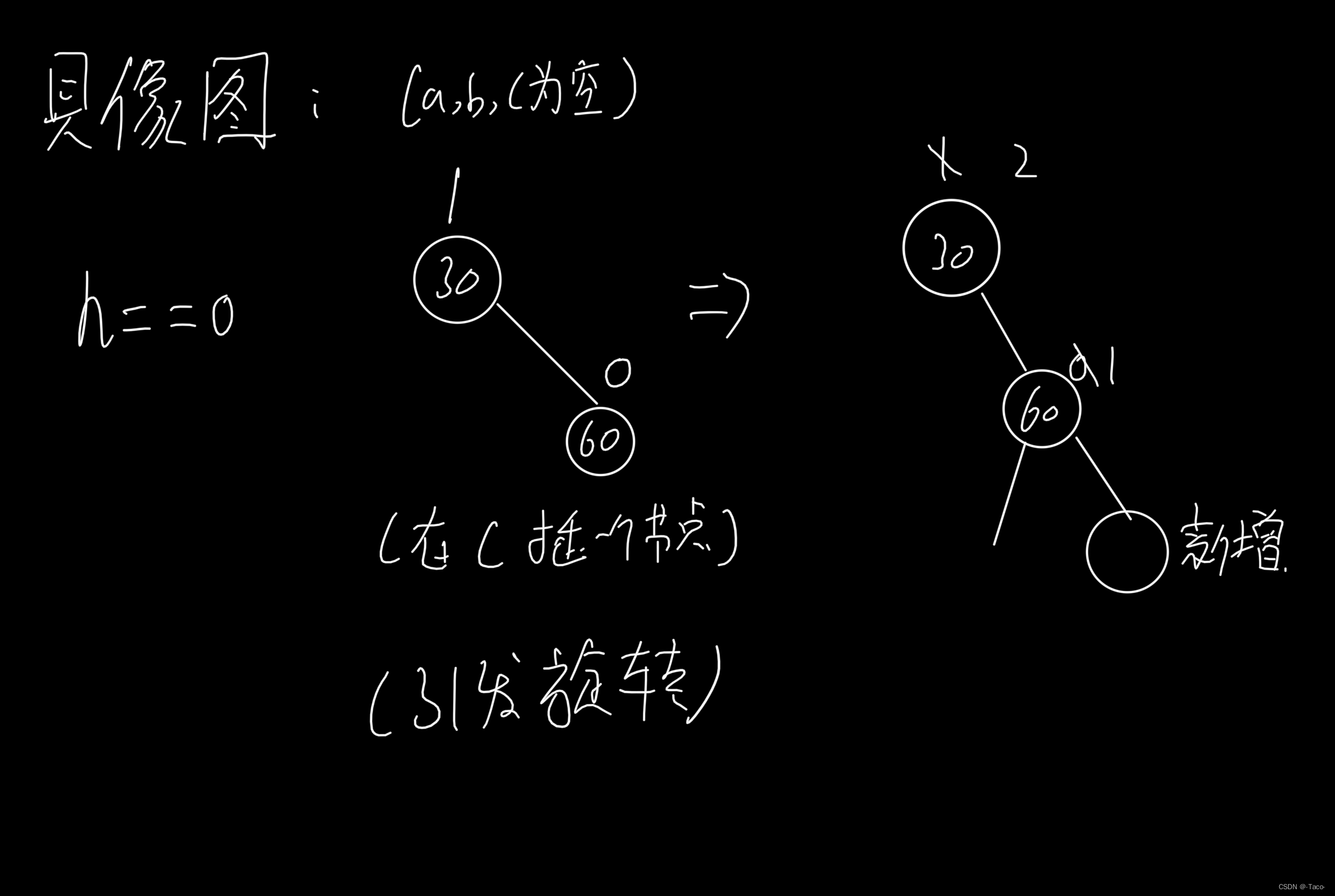
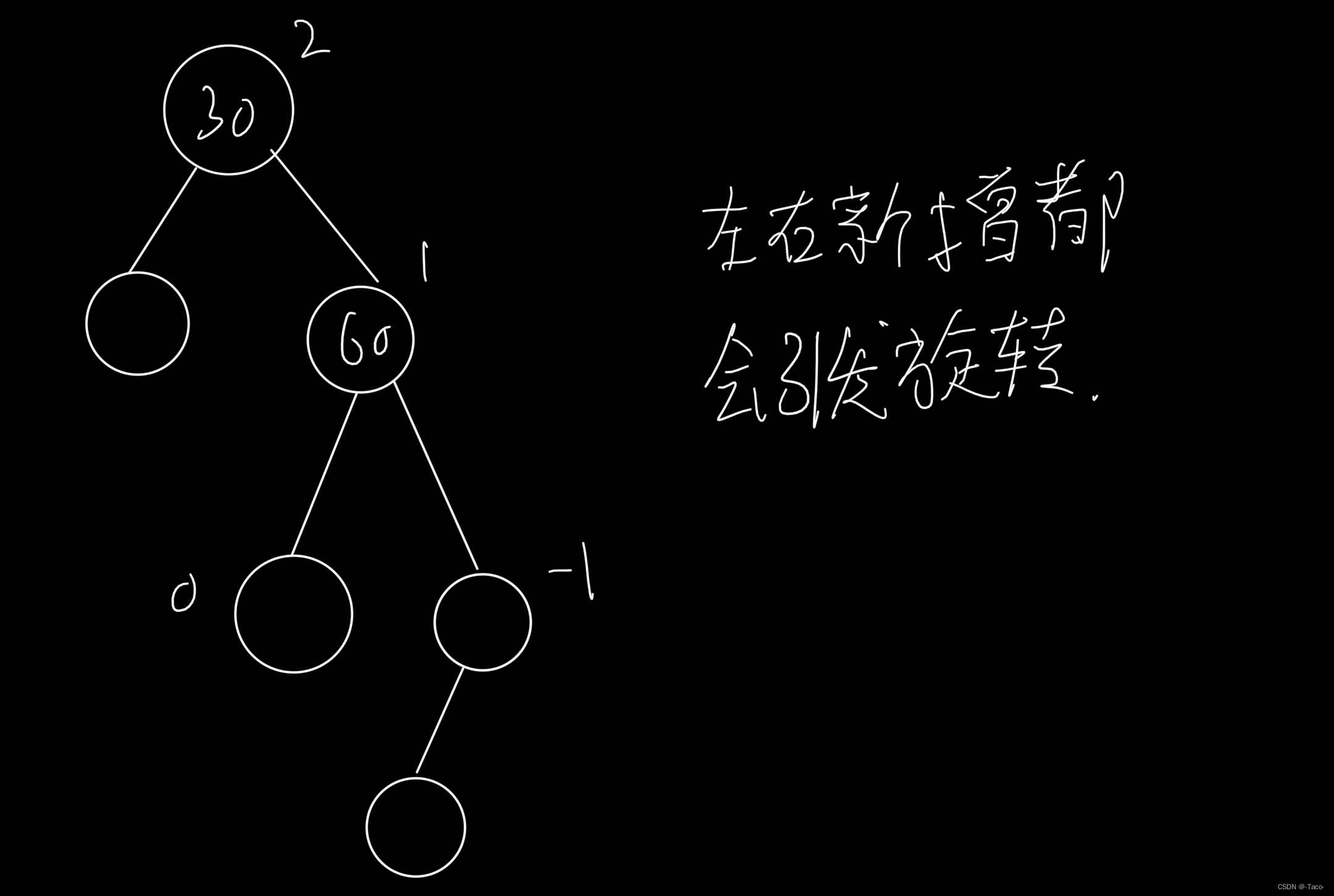
a和b是x，y，z中的任意一种，c是固定的，因为c是a，b这两种的话，c自身就会发生旋转，a，b处各有三种（x，y，z）组合起来就是9种，在c的任意位置新增，都会引发30的旋转；
变化的规则就是让b成为30的右边，30变成60的右边；
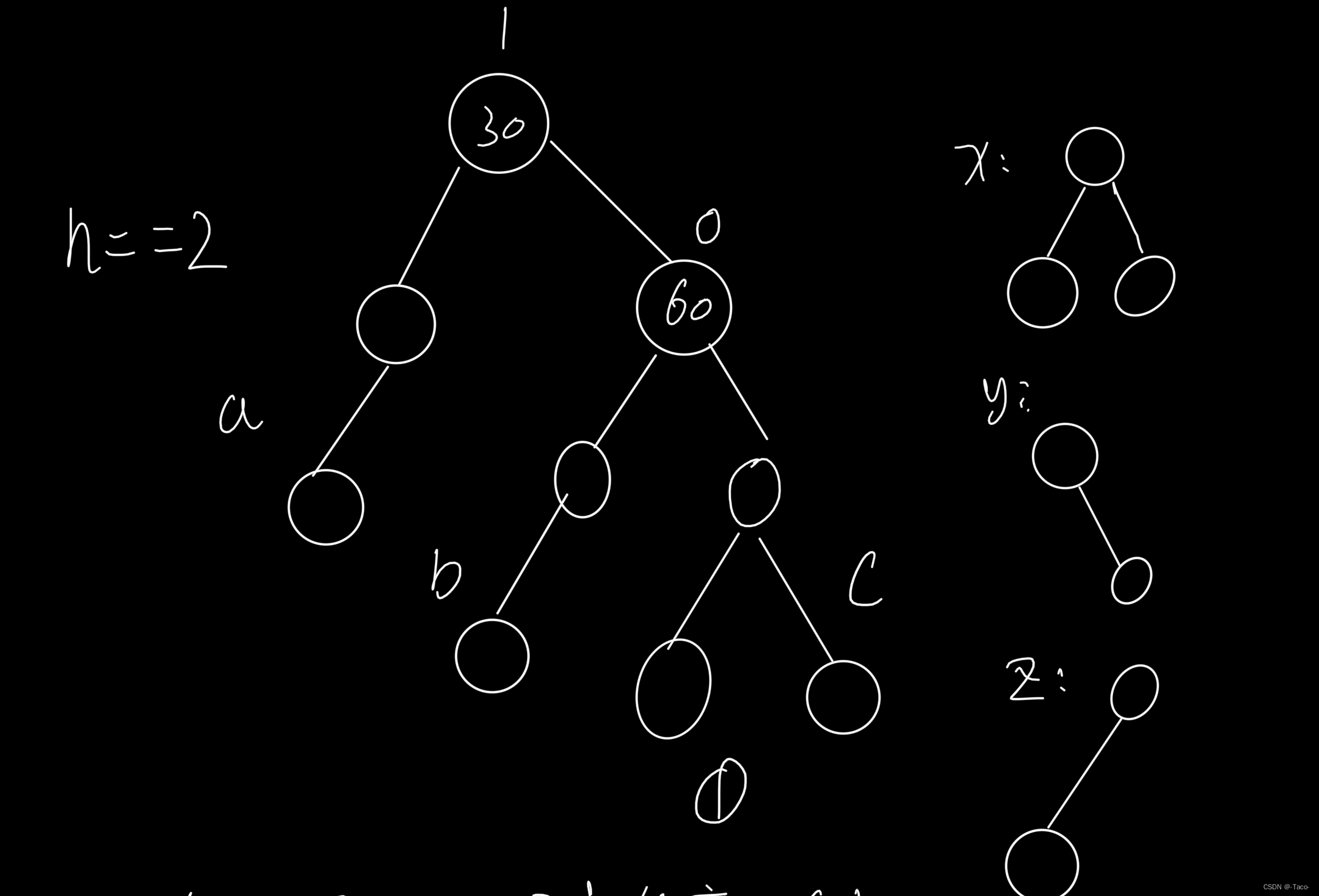
当h==2时的图形形状，c的最后两个结点，分别可以连接左右两个结点都会让30旋转，所以当h==2的时候会出现4*9=36种结果；
h==3，只会更多，这里就不一一的统计了；列举只会是无穷无尽的，我们对旋转的处理只能通过表象分析；本质都是引发的parent因子变成2，右边高，需要旋转；
下面的高度是几不重要，反正下面a，b都是平衡树，说明插入就出现问题了，c不是平衡树，到不了30，自己就会发生旋转。只会是c到临界值了，没有出问题，一路往上更新，更新到30；只能通过分析共性，它们的处理方式都是一样的；
我们代码模拟实现左旋：
根据图这样写可以吗？
这样写的话，互相找不到了；
这里修改之后，让它们节点之间可以互相找到，这里改正确了吗？
不正确的，这样写的话，如果这个左旋转的情况是一个树的子树，那么它的parent的parent是谁？
没有解决，它跟新节点直接没有取得联系：
所以修改完之后的左旋代码：
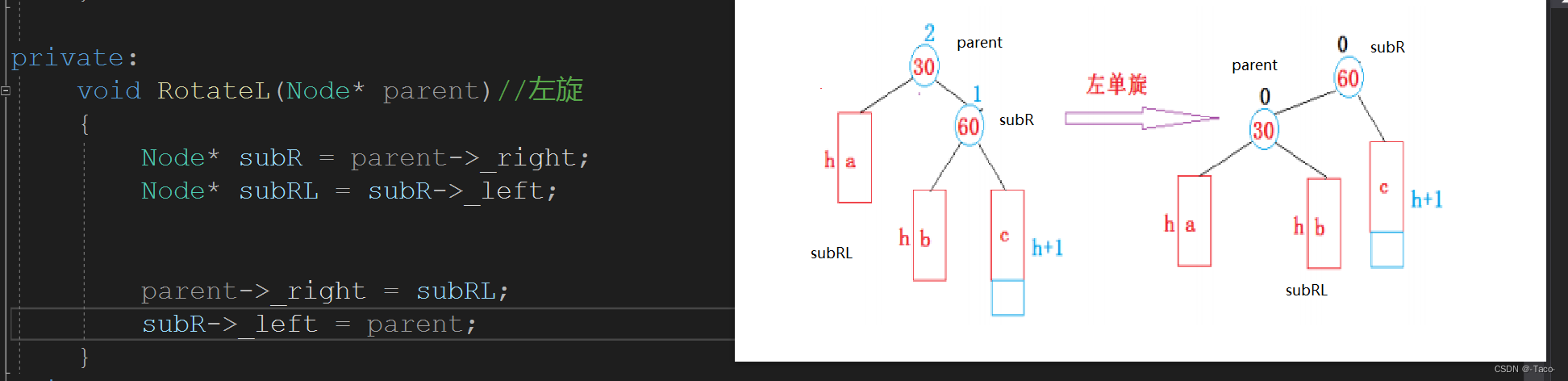
void RotateL(Node* parent)//左旋
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//注意顺序；
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
//subRL->_parent = parent;
//a,b,c都是高度为L的树，但是L可以=0
//c的L之前分析过不会为0，如果L=0的话
//这里subRL就发生了空指针解引用的问题
//这里记录一下ppNode：
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
//还差subR的父亲；（这里有两种情况，parent是根）
//parent是子树的根
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;//根是没有父亲的
}
else//子树的情况，上面还有个节点，假设为ppNode
{
//之前是parent的parent的ppNode，但是现在parent的parent是subR
//所以就需要一个值记录之前，没改节点之前的parent的parent，之后在用现在的subR去连接它
//但是是ppNode的左还是右还是不清楚；还得讨论
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
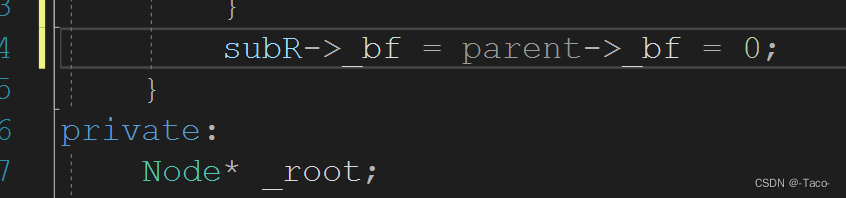
subR->_bf = parent->_bf = 0;
}
这里再修改一下平衡因子就完成了左旋：只有parent和subR的平衡因子变化了；
在这个单旋中这两个的平衡因子都是0；
2.
新节点插入较高左子树的左侧
---
左左：右单旋
右旋跟左旋是完全一致的；
a，b，c是h>=0平衡树，
void RotateR(Node* parent)//右旋
{
//右旋前
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
//开始旋转
Node* ppNode = parent->_parent;//先保存一下之前parent的parent，之后用来连接旋转后的subL
//但是不知道这之前parent的ppnode，我们下面的树是它的左树还是右树，就得分情况讨论
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
//说明_root要变成subL
_root = subL;
subL->_parent = nullptr;//不置空就会局部形成环状结构
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
subL->_bf = parent->_bf = 0;
} 
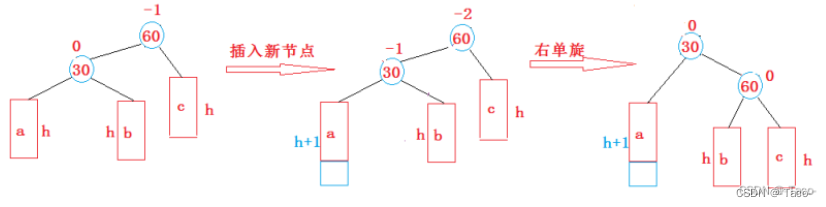
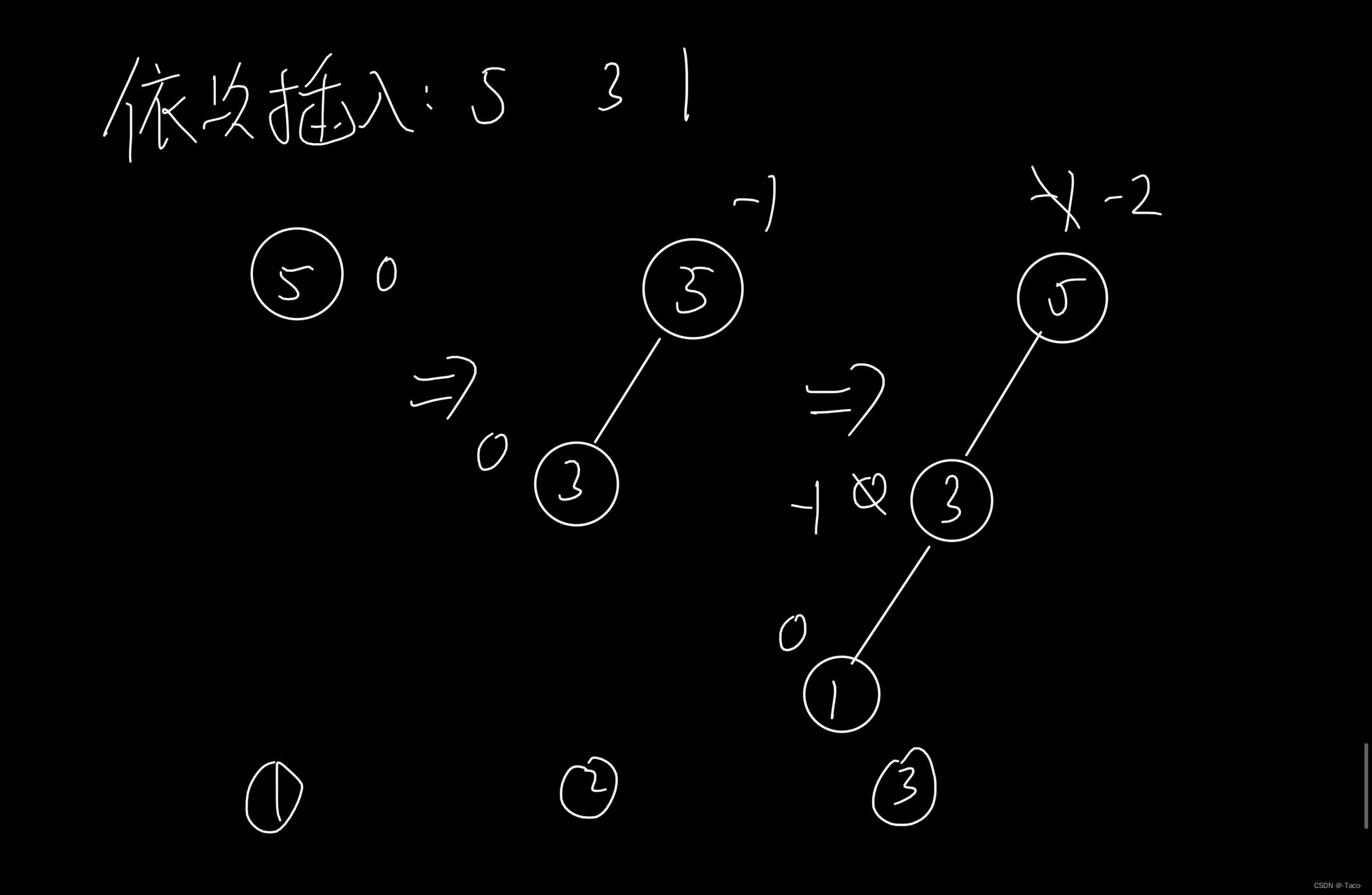
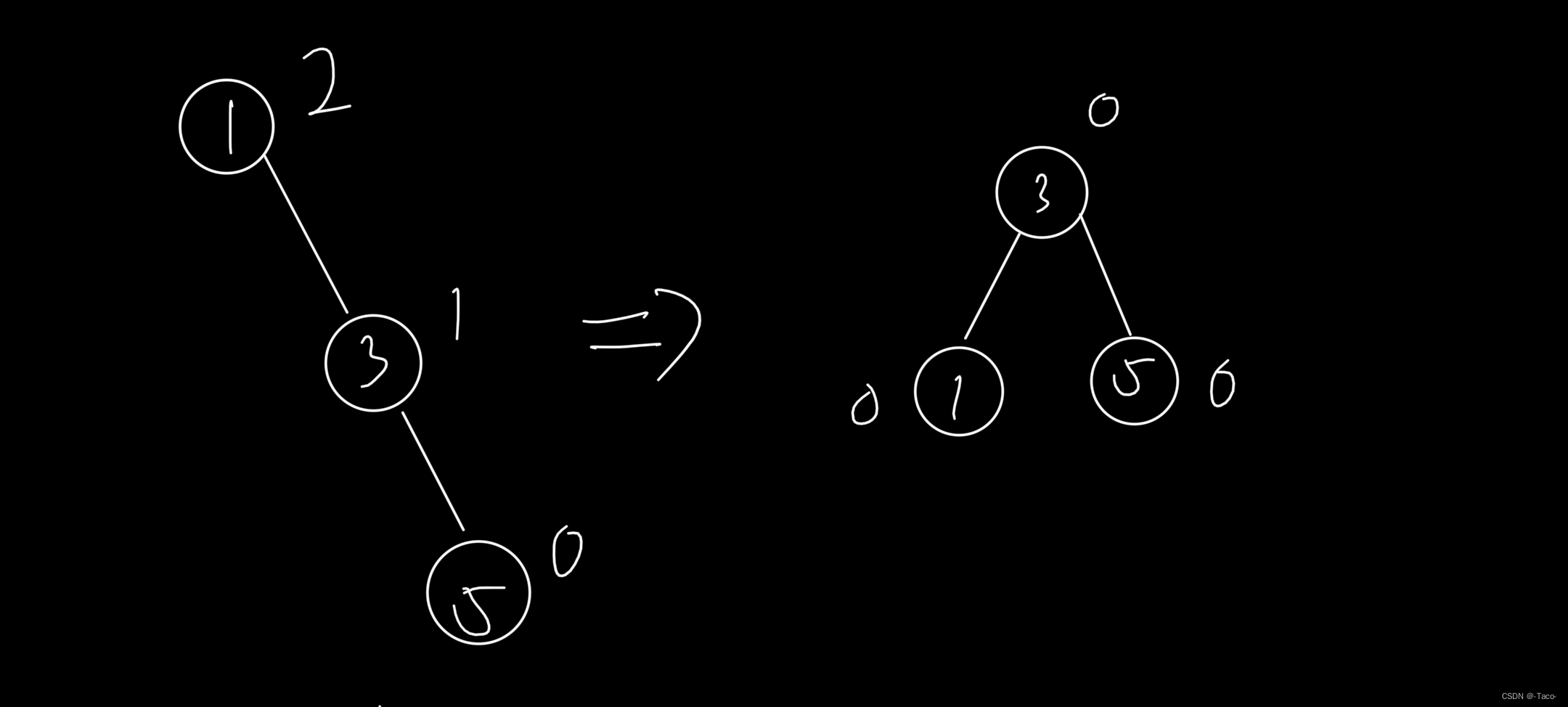
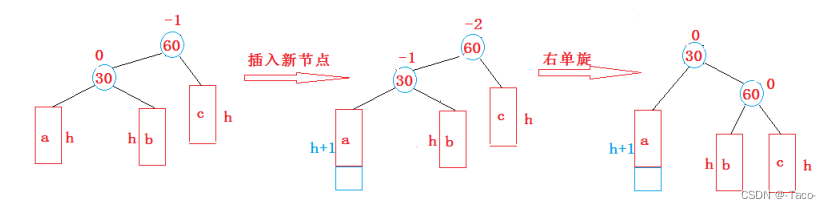
在a插入，高度变为h+1，这时是一个右单旋，如果在b插入b变成h+1，这时候右单旋，就不是平衡树了，
这里就从左边高变成了右边高 ，旋转成了一个对称的树；单选只能是来回摇摆；
所以单纯的左边高就用右旋，单纯的右边高就用左旋；
如果是类似上面的折线路径，就需要双旋来解决了；
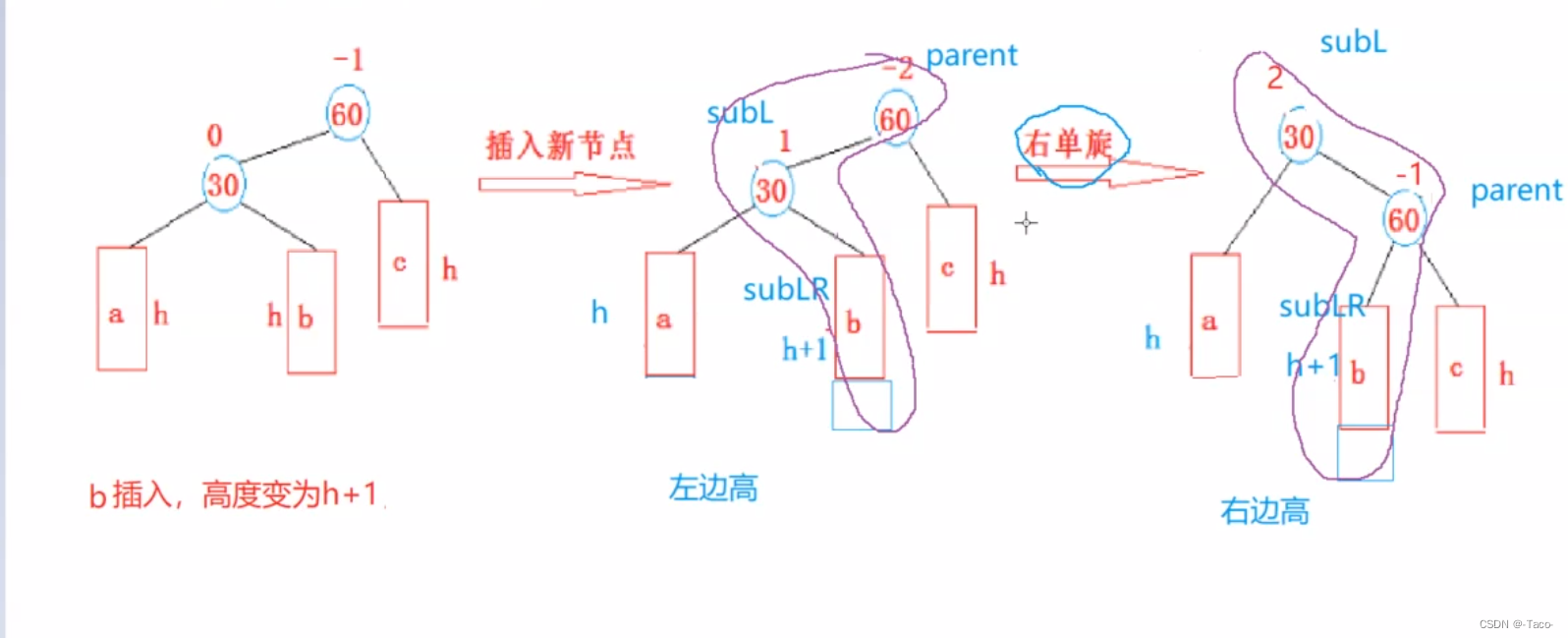
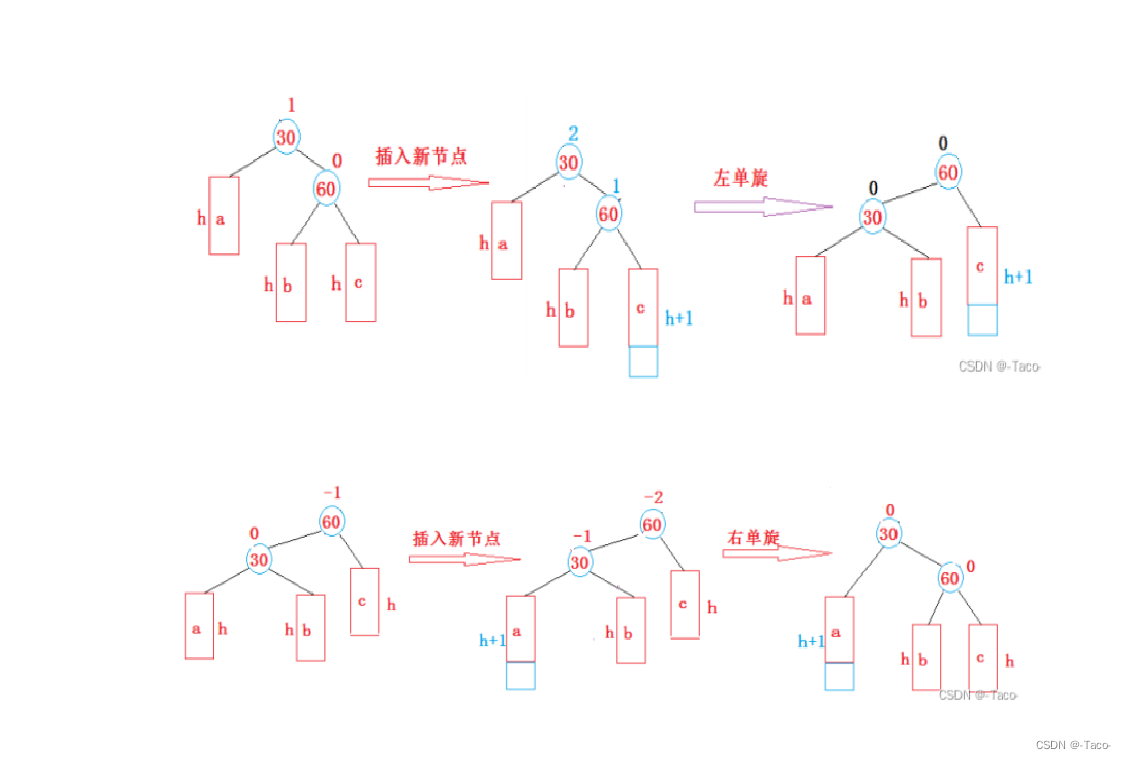
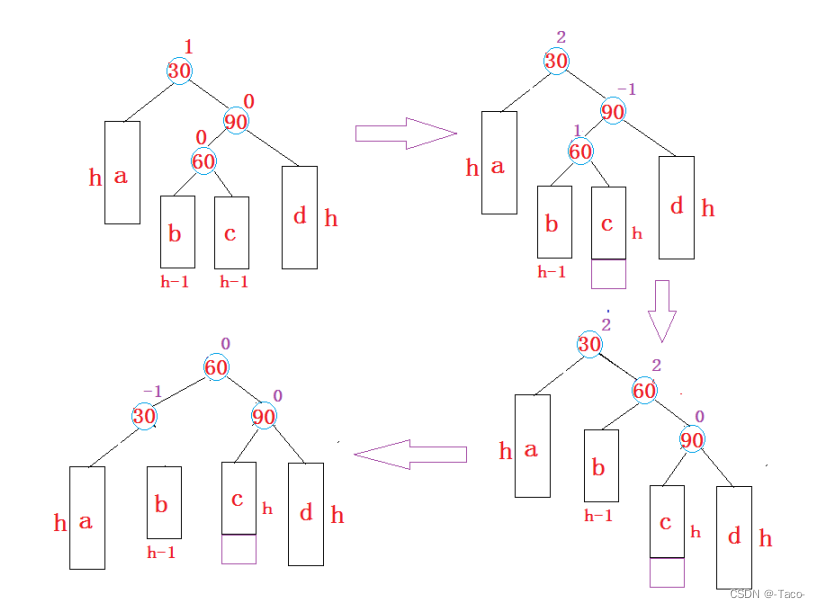
思路是：先对30左单旋，把它换成直线形，之后再以60为结点再旋转，这就是就是上面1和2 的情况，是左边高用右单选；代码可以复用之前写过的；下面我们看3。多旋的分析；
3.
新节点插入较高左子树的右侧
---
左右：先左单旋再右单旋
60是上面2多选情况下b的展开，不展开的话不好分析；
在b或者c插入，都会引起b或者c的高度变为h，都会引发双旋；（b或者c的插入都会引发60变成-1/1之后30变成1，90变成-2，开始双旋）
将双旋变成单旋后再旋转，即：
先对
30
进行左单旋，然后再对
90
进行右单旋
，旋转完成后再
考虑平衡因子的更新。
b插入就是上面的平衡因子，如果是c从插入，旋转的过程也会发生一些改变，b就变成了h-1，c是h
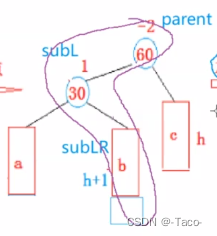
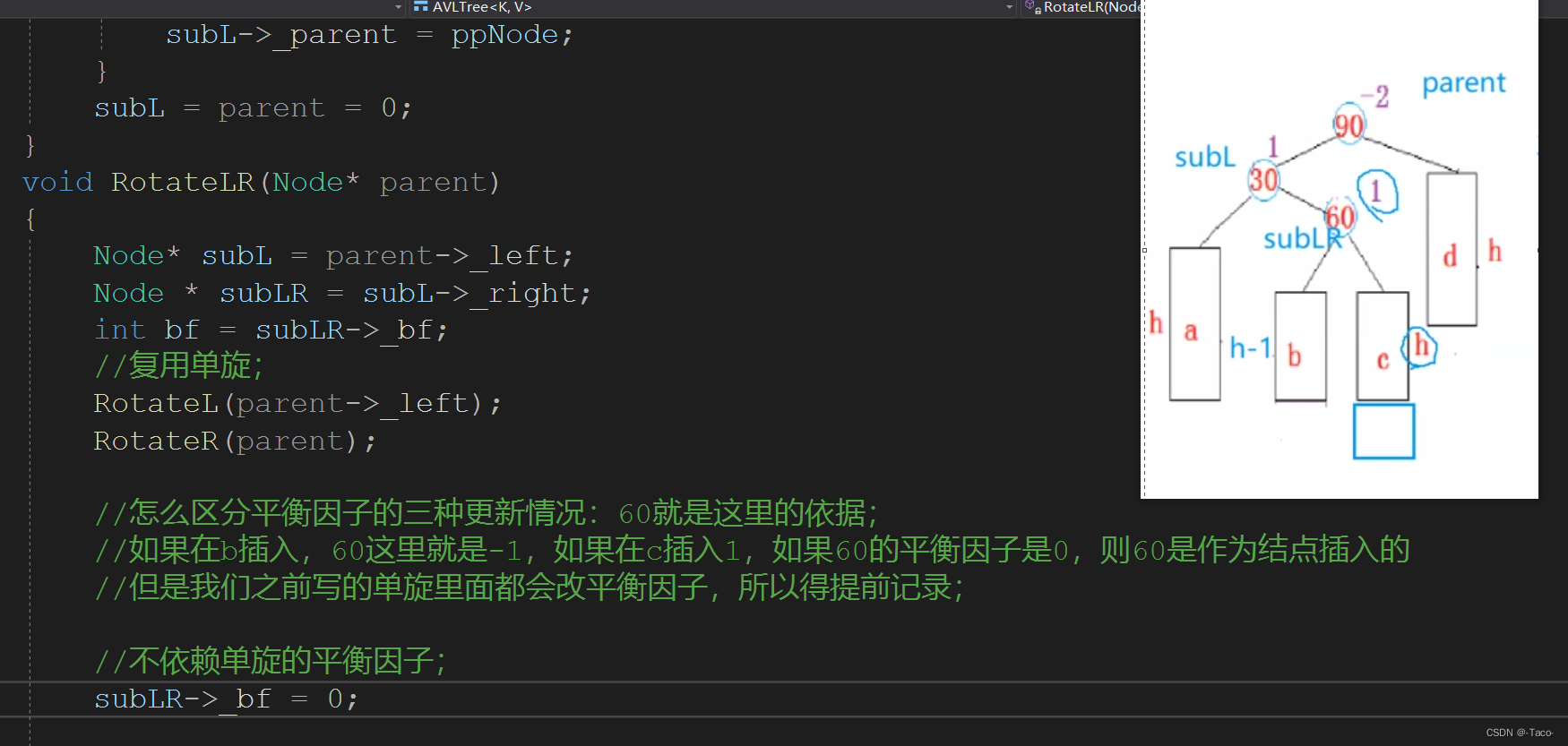
两个平衡因子是有区别的，所以在更新平衡因子的时候就需要特定的更新平衡因子；（60为什么是0？左边是h+1，右边也是h+1）
h是0时候也会出现问题；（60作为新增的结点）
这里的平衡因子是 0 0 0
上面的三种情况都是旋转过程不变，但是平衡因子有区别；
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node * subLR = subL->_right;
int bf = subLR->_bf;
//复用单旋；
RotateL(parent->_left);
RotateR(parent);
//怎么区分平衡因子的三种更新情况：60就是这里的依据；
//如果在b插入，60这里就是-1，如果在c插入1，如果60的平衡因子是0，则60是作为结点插入的
//但是我们之前写的单旋里面都会改平衡因子，所以得提前记录；
//不依赖单旋的平衡因子；
subLR->_bf = 0;
if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
}
else if(bf==0)
{
parent->_bf = 0;
subL->_bf = 0;
}
else
{
assert(false);
}
}
4.
新节点插入较高右子树的左侧
---
右左：先右单旋再左单旋
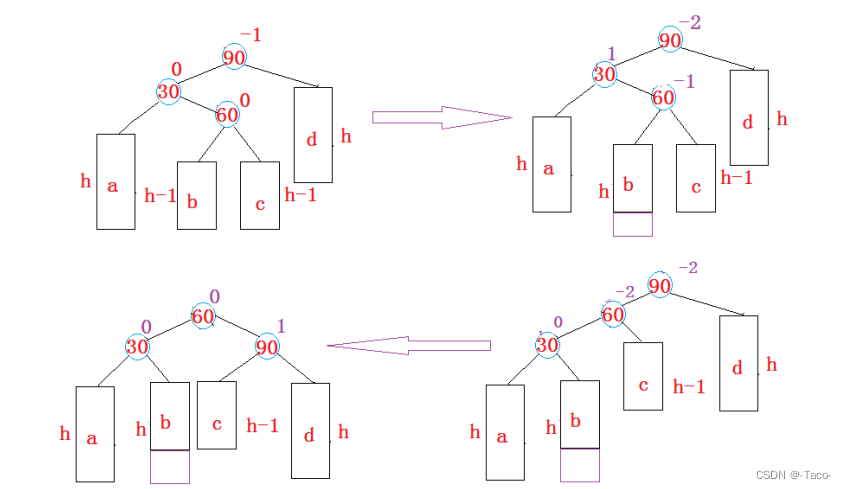
插入同3分析，跟3旋转顺序相反
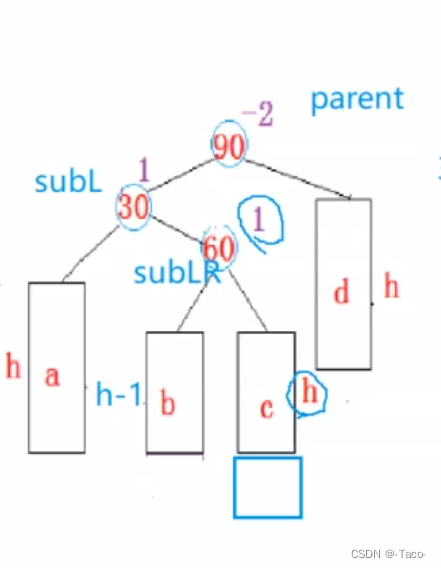
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);//以90为根进行右单选；
RotateL(parent);//以30为根进行左选；
//subRL永远都是0
subRL->_bf = 0;
if (bf == 1)//c插入
{
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
}
else if (bf==0)
{
parent->_bf=0;
subR->_bf = 0;
}
else
{
assert(false);
}
}旋转的价值和意义：
1.平衡
2.降高度（高度恢复到插入之前的样子）
将
总的插入：
#pragma once
#include<iostream>
#include<assert.h>
#include<algorithm>
#include<time.h>
using namespace std;
template<class K,class V>
struct AVLTreeNode
{
AVLTreeNode<K, V>* _left;
AVLTreeNode<K, V>* _right;
AVLTreeNode<K, V>* _parent;
pair<K, V>_kv;
int _bf;//balance factor:平衡因子(设计时非必须）
AVLTreeNode(const pair<K, V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
};
template<class K,class V>
struct AVLTree
{
typedef AVLTreeNode<K, V> Node;
public:
//先插入之后再平衡
//写的时候能用非递归就尽量用非递归；
bool Insert(const pair<K,V>&kv)//插入的时候本质上还是跟搜索树是一样的；(大就往右走，小就往左走）
{
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)//让cur走到空的位置，parent指向cur
{
if (cur->_kv.first < kv.first)//插入的值比这个大走右边
{
parent = cur;
cur = cur->_right;
}
else if(cur->_kv.first>kv.first)//插入的值比要比较的值小，就走左边
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//这里就该插入了：
cur = new Node(kv);
if (parent->_kv.first < kv.first)//插入的值比这个值要大就链接在右边
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//parent是怎么连接的，插入第一个节点不需要考虑parent；
cur->_parent = parent;//三叉链
//控制平衡（有可能插入的时候已经平衡了，有可能也没平衡）
//新插入节点的平衡因子肯定是0，之后沿着这个节点往上去更新平衡因子;
//1.更新平衡因子
while (parent)//最坏的情况有可能更新到根节点；（只有根节点的父亲为null）
{
if (cur == parent->_right)
{
parent->_bf++;
}
else
{
parent->_bf--;
}
if (parent->_bf == 0)
{
break;
}
else if (abs(parent->_bf)==1)
{
//继续更新，三叉链；
parent = parent->_parent;
cur = cur->_parent;
}
else if (abs(parent->_bf) == 2)//绝对值，求出来bf为±2；
{
//说明parent所在的子树已经不平衡了，需要旋转处理；
if (parent->_bf == 2 && cur->_bf == 1)
{
RotateL(parent);
}
else if ((parent->_bf == -2 && cur->_bf == -1))
{
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
RotateRL(parent);
}
else
{
assert(false);
}
break;
}
else
{
//parent是大于2的，说明插入之前是出现问题的，
assert(false);//报错；
}
}
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()
{
return _IsBalance(_root);
}
private:
bool _IsBalance(Node* root)
{
if (root == nullptr)
return true;
int leftH = Height(root->_left);
int rightH = Height(root->_right);
int diff = rightH - leftH;
return abs(diff) < 2
&&_IsBalance(root->_right)
&&_IsBalance(root->_left);//如果小于2就是真，大于等于2就是假；
//不能只判断自己，还要递归判断自己的左右子树；
}
int Height(Node* root)//是一个后续遍历，先左右子树再求自己
{
if (root == nullptr)
return 0;
int leftHT = Height(root->_left);
int rightHT = Height(root->_right);
return max(leftHT, rightHT) + 1;
}
void RotateL(Node* parent)//左旋
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//注意顺序；
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
//subRL->_parent = parent;
//a,b,c都是高度为L的树，但是L可以=0
//c的L之前分析过不会为0，如果L=0的话
//这里subRL就发生了空指针解引用的问题
//这里记录一下ppNode：
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
//还差subR的父亲；（这里有两种情况，parent是根）
//parent是子树的根
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;//根是没有父亲的
}
else//子树的情况，上面还有个节点，假设为ppNode
{
//之前是parent的parent的ppNode，但是现在parent的parent是subR
//所以就需要一个值记录之前，没改节点之前的parent的parent，之后在用现在的subR去连接它
//但是是ppNode的左还是右还是不清楚；还得讨论
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
subR->_bf = parent->_bf = 0;
}
void RotateR(Node* parent)//右旋
{
//右旋前
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
//开始旋转
Node* ppNode = parent->_parent;//先保存一下之前parent的parent，之后用来连接旋转后的subL
//但是不知道这之前parent的ppnode，我们下面的树是它的左树还是右树，就得分情况讨论
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
//说明_root要变成subL
_root = subL;
subL->_parent = nullptr;//不置空就会局部形成环状结构
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
subL->_bf = parent->_bf = 0;
}
void RotateLR(Node* parent)
{
Node* subL = parent->_left;
Node * subLR = subL->_right;
int bf = subLR->_bf;
//复用单旋；
RotateL(parent->_left);
RotateR(parent);
//怎么区分平衡因子的三种更新情况：60就是这里的依据；
//如果在b插入，60这里就是-1，如果在c插入1，如果60的平衡因子是0，则60是作为结点插入的
//但是我们之前写的单旋里面都会改平衡因子，所以得提前记录；
//不依赖单旋的平衡因子；
subLR->_bf = 0;
if (bf == 1)
{
parent->_bf = 0;
subL->_bf = -1;
}
else if (bf == -1)
{
parent->_bf = 1;
subL->_bf = 0;
}
else if(bf==0)
{
parent->_bf = 0;
subL->_bf = 0;
}
else
{
assert(false);
}
}
void RotateRL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
int bf = subRL->_bf;
RotateR(parent->_right);//以90为根进行右单选；
RotateL(parent);//以30为根进行左选；
//subRL永远都是0
subRL->_bf = 0;
if (bf == 1)//c插入
{
subR->_bf = 0;
parent->_bf = -1;
}
else if (bf == -1)
{
subR->_bf = 1;
parent->_bf = 0;
}
else if (bf==0)
{
parent->_bf=0;
subR->_bf = 0;
}
else
{
assert(false);
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
private:
Node* _root=nullptr;
};
void TestAVLTree1()
{
int a[] = { 16,3,7,11,9,26,18,14,15 };
AVLTree<int, int>t1;
for (auto e : a)
{
t1.Insert(make_pair(e,e));
}
t1.InOrder();
cout << "Isbalance:"<<t1.IsBalance()<<endl;
}
//也可能树是平衡的，平衡因子不对；
void TestAVLTree2()
{
size_t N = 10000;
AVLTree<int, int> t1;
srand(time(0));
for (size_t i = 0; i < N; i++)
{
int x = rand();
t1.Insert(make_pair(x,i));
}
cout << "IsBalance:" << t1.IsBalance() << endl;
}
AVL
树的验证
单纯的验证平衡因子不是特别的科学，因为这就是你自己设计的，所以不好拿来验证；
高度是可以用来验证的，写一个高度的函数来验证；
AVL
树的删除
(
了解
)
因为
AVL
树也是二叉搜索树，可按照二叉搜索树的方式将节点删除，然后再更新平衡因子，只不
错与删除不同的时，删除节点后的平衡因子更新，最差情况下一直要调整到根节点的位置。
AVL
树的性能
AVL
树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过
1
，这
样可以保证查询时高效的时间复杂度，即
$log_2 (N)$
。但是如果要对
AVL
树做一些结构修改的操
作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，
有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数
据的个数为静态的
(
即不会改变
)
，可以考虑
AVL
树，但一个结构经常修改，就不太适合。
AVLTree:要求左右高度差不超过1（太严格了，意味着旋转就会更多次，旋转虽然是O（1）次数，但是旋转仍然会损失性能）
红黑树：最长路径不超过最短路径的2倍；（不严格的近似平衡）达到的效果：相对而言插入同样的数据AVL的旋转更多，红黑树旋转更少；
单次的查找红黑树可能略慢一点，但是这是最坏的情况，大多数还是差不多效果的；
红黑树
红黑树的概念
红黑树
，是一种
二叉搜索树
，但
在每个结点上增加一个存储位表示结点的颜色，可以是
Red
或
Black
。 通过对
任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路
径会比其他路径长出俩倍
，因而是
接近平衡
的。
这条树有11条路径（看尾（空结点））
红黑树的性质
1.
每个结点不是红色就是黑色
2.
根节点是黑色的
3.
如果一个节点是红色的，则它的两个孩子结点是黑色的
（树中没有连续的红色节点)
4.
对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点
(每条路径的黑色节点数量相等)
5.
每个叶子（NIL）结点都是黑色的
(
此处的叶子结点指的是
空结点
)
为什么满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径节点
个数的两倍？
每条路径都有相同的黑的，极限的最短就是全黑，极限的最长一黑一红
跟AVL一样我们只写它的插入：
前面的这部分几乎可以复用，只不过这里没有平衡因子，只有_col
颜色的定义使用枚举，只有两种颜色：红黑；
enum Colour
{
RED,
BlACK
};
template<class K,class V>
struct RedBlackNode
{
//这个跟AVL的结点设计差不多，都需要三叉链
RedBlackNode<K, V>* _left;
RedBlackNode<K, V>* _right;
RedBlackNode<K, V>* _parent;
pair<K, V> _kv;
Colour _col;
RedBlackNode(const pair<K, V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
{}
};
//都是三叉链插入的过程应该是很类似于AVL的
template<class K, class V>
struct RedBlackTree
{
typedef RedBlackNode<K, V> Node;
public:
//先插入之后再平衡
//写的时候能用非递归就尽量用非递归；
bool Insert(const pair<K, V>& kv)//插入的时候本质上还是跟搜索树是一样的；(大就往右走，小就往左走）
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BlACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)//让cur走到空的位置，parent指向cur
{
if (cur->_kv.first < kv.first)//插入的值比这个大走右边
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)//插入的值比要比较的值小，就走左边
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//这里就该插入了：
cur = new Node(kv);
if (parent->_kv.first < kv.first)//插入的值比这个值要大就链接在右边
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//parent是怎么连接的，插入第一个节点不需要考虑parent；
cur->_parent = parent;//三叉链
}
private:
Node* _root = nullptr;
};
新插入的结点是去从黑插入还是从红插入：
--是插入一个红色
比如想插入一个29进去，插入黑就违反规则4，插入一个红就违法规则3，但是很明显3的后果小，而且如果29插入到11这里，符合规则，完全不用处理；（黑大插入就麻烦大了）
黑红树处理问题的两种方法：（红黑树平常在处理的时候，不看最长路径和最短路径，虽然它是靠着这个理论实现的，但是它是依靠着上面的变色方案来间接的达到最长路径不超过最短路径的二倍这个效果）
所以它的规则就是变色+旋转；
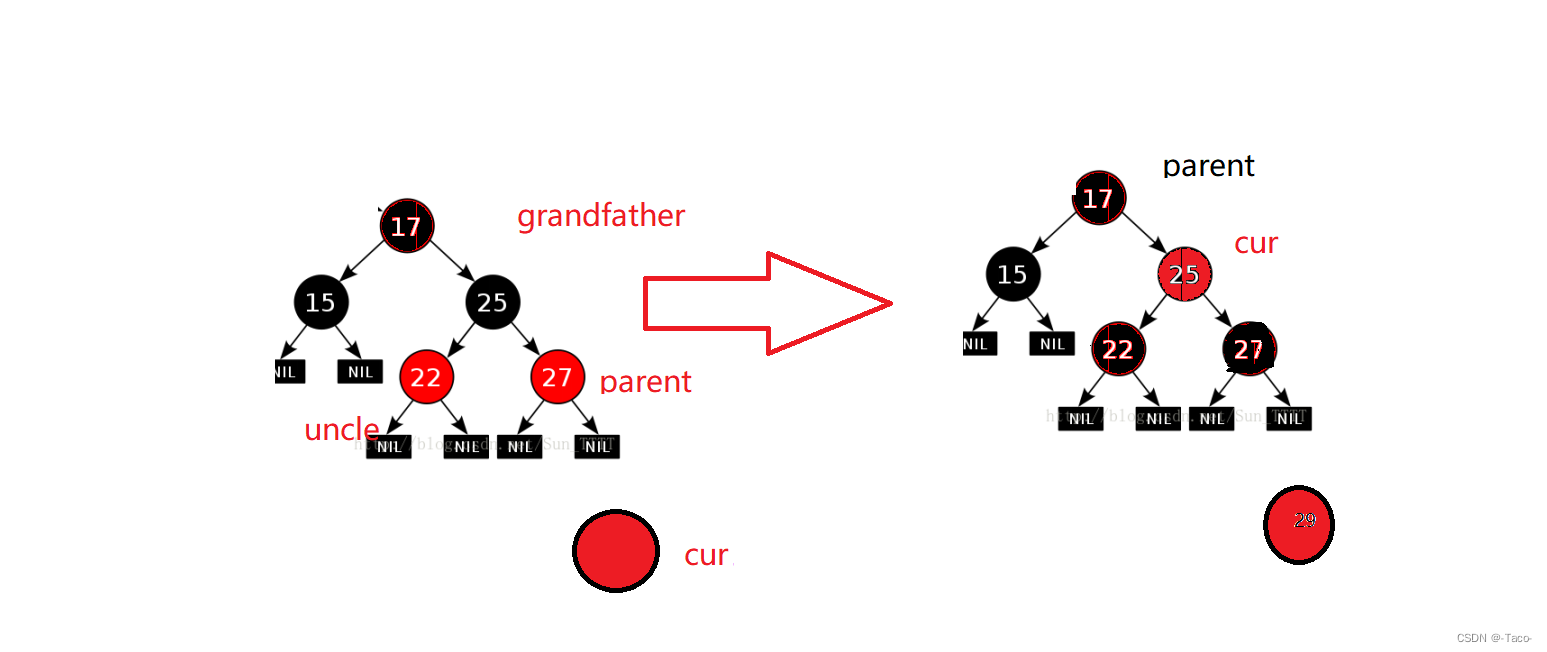
遇事不决找叔叔（叔叔存在且为红），叔叔跟父亲一起背锅一起变黑；
parent uncle变黑，grandfather变红，继续往上处理；
情况一
:
cur
为红，
p
为红，
g
为黑，
u
存在且为红
cur:当前的位置，p：parent节点，g：grandfather节点，u：uncle
注意:此处所看到的树，可能是一棵完整的树，也可能是一棵子树
（变色）
a/b/c/d/e是子树；
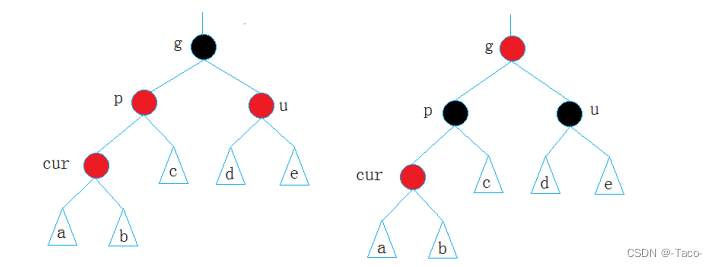
如果g是根节点，调整完成后，需要将g改为黑色
如果g是子树，g一定有双亲，且g的双亲如果是红色，需要继续向上调整
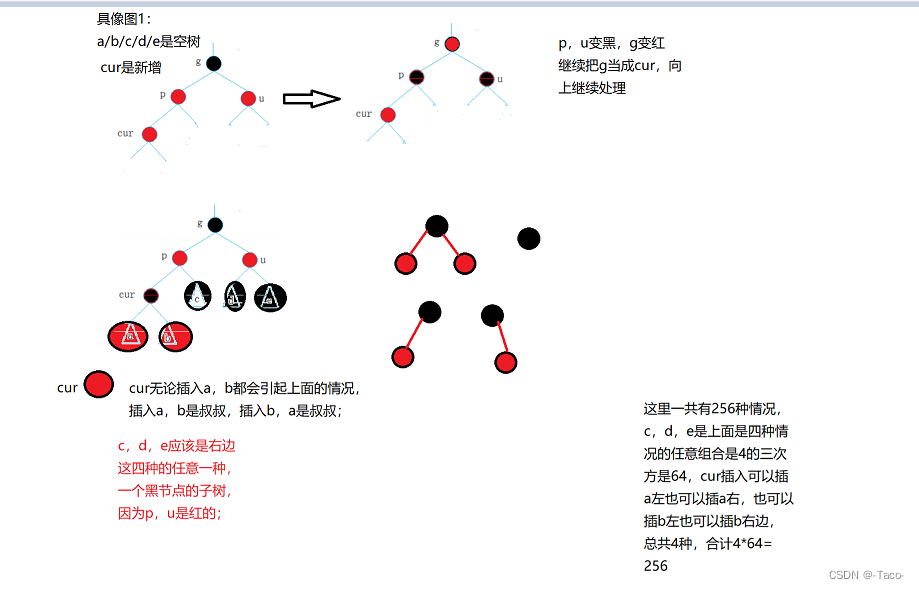
cur可以是黑的，下面是新插，以及cur的下面下面是黑的，cur下面下面下面的是新增，就又多了很多倍，无穷无尽；
所以cur不一定是新增，也可能是由下面变上来的，因为下面插入一个cur，p和u是红色，grandfather是黑色，parent和uncle就边黑，grandfather就变红（只要不是根结点），所以你也不清楚下面到底有几层，我们不用关系下面有几层，从哪里变来的，只要满足p和u是红，g是黑，就变色， 红黑树里，变化最大的就是u，u存在且为红，就变黑，g变红继续向上调整，这就是我们的大体思路；（因为要保持子树黑色节点的个数不变）是根节点就黑，保证根节点是黑色；新增可以在上面的类型a，b左右都可以；
cur
和
p
均为红，违反了性质三，此处能否将
p
直接改为黑？
解决方式：将
p,u
改为黑，
g
改为红，然后把
g
当成
cur
，继续向上调整。
情况二
:
cur
为红，
p
为红，
g
为黑，
u
不存在
/u
存在且为黑
（旋转+变色）
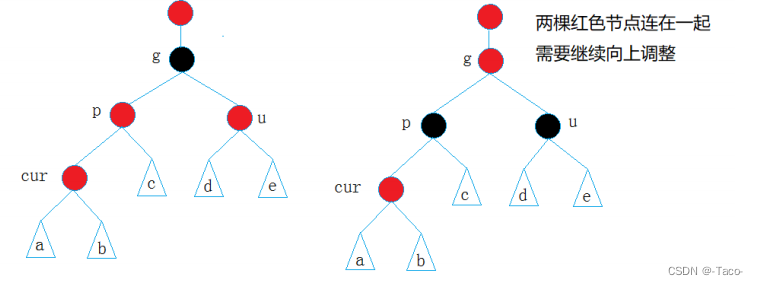
说明:u的情况有两种
1.如果u节点不存在，则cur一定是新插入节点，因为如果cur不是新插入节点，则cur和p一定有一个节点的颜色是黑色，就不满足性质4∶每条路径黑色节点个数相同。
2.如果u节点存在，则其一定是黑色的，那么cur节点原来的颜色一定是黑色的，现在看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由黑色改成红色。
p
为
g
的左孩子，
cur
为
p
的左孩子，则进行右单旋转；相反，
p
为
g
的右孩子，
cur
为
p
的右孩子，则进行左单旋转
p
、
g
变色
--p
变黑，
g
变红
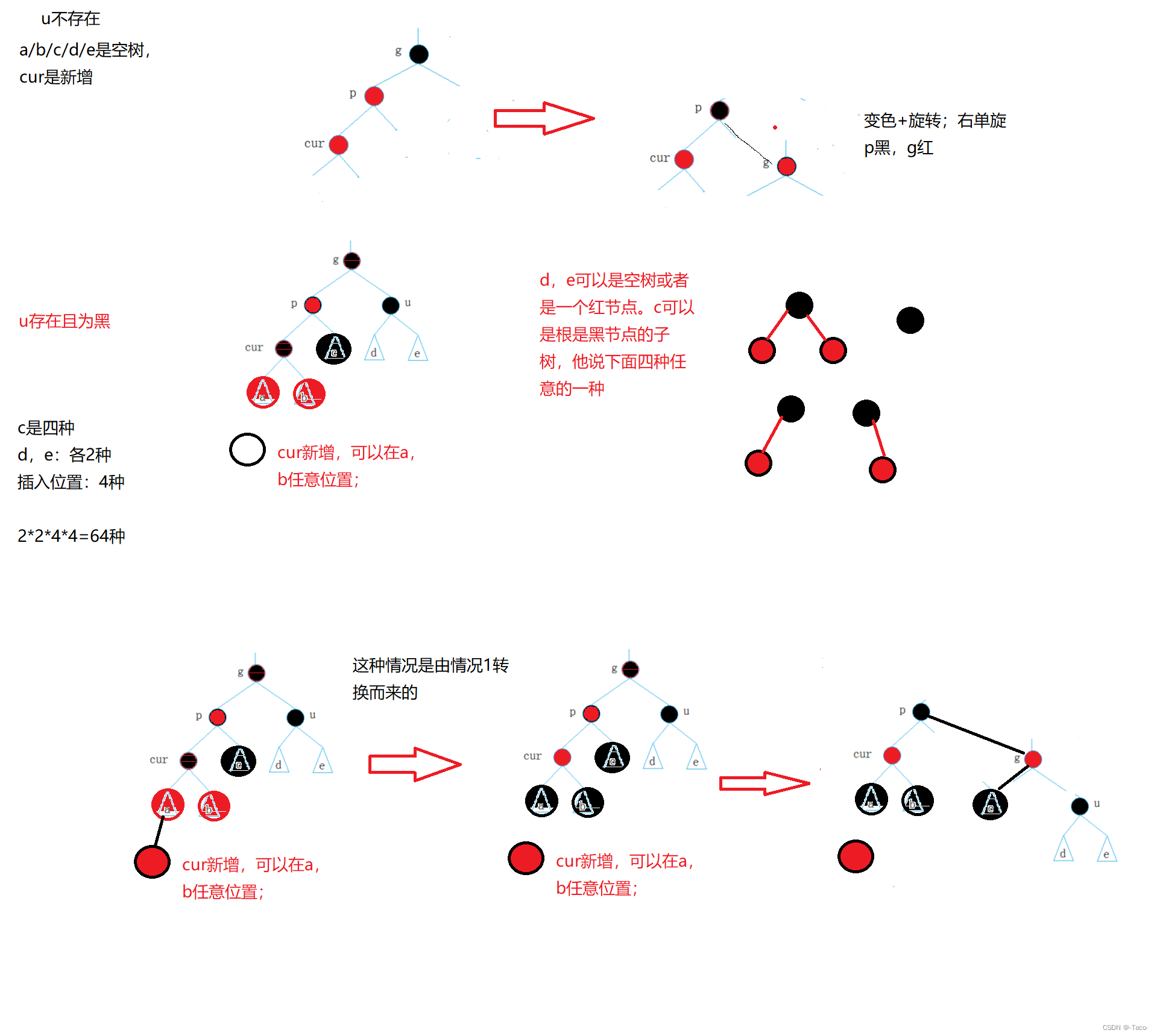
处理完就结束了；
情况三
:
cur
为红，
p
为红，
g
为黑，
u
不存在
/u
存在且为黑---双旋+变色
p
为
g
的左孩子，
cur
为
p
的右孩子，则针对
p
做左单旋转；相反，
p
为
g
的右孩子，
cur
为
p
的左孩子，则针对
p
做右单旋转
则转换成了情况
2
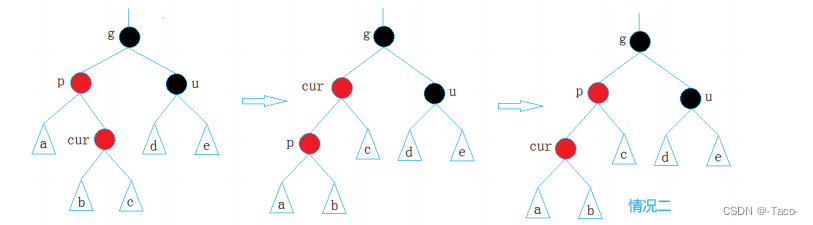
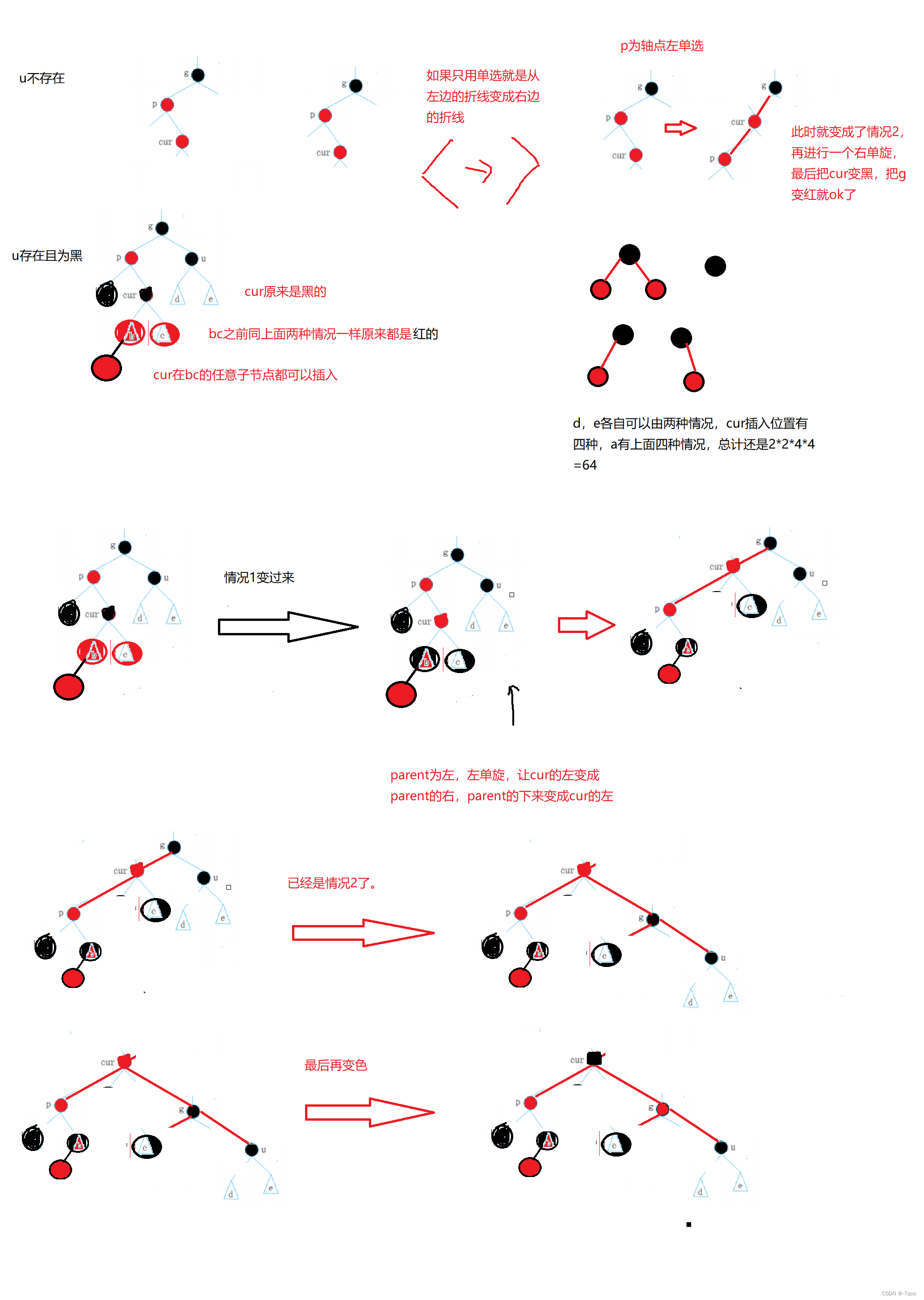
无论是局部还是整个树，这么改完就不会有问题了；
针对每种情况进行相应的处理即可。
（红黑树的关键是叔叔（u），u存在且为红，变色继续往上处理，AVL树很严格。稍微改变就得旋转，如果u不存在或者u存在且为黑，旋转+变色，四转旋转，是单旋还是双旋转）
下面是插入的整体代码，包括测试的时候需要注意的前序递归
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
enum Colour
{
RED,
BlACK
};
template<class K,class V>
struct RedBlackNode
{
//这个跟AVL的结点设计差不多，都需要三叉链
RedBlackNode<K, V>* _left;
RedBlackNode<K, V>* _right;
RedBlackNode<K, V>* _parent;
pair<K, V> _kv;
Colour _col;
RedBlackNode(const pair<K, V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
{}
};
//都是三叉链插入的过程应该是很类似于AVL的
template<class K, class V>
struct RedBlackTree
{
typedef RedBlackNode<K, V> Node;
public:
//先插入之后再平衡
//写的时候能用非递归就尽量用非递归；
bool Insert(const pair<K, V>& kv)//插入的时候本质上还是跟搜索树是一样的；(大就往右走，小就往左走）
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = BlACK;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)//让cur走到空的位置，parent指向cur
{
if (cur->_kv.first < kv.first)//插入的值比这个大走右边
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)//插入的值比要比较的值小，就走左边
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
//这里就该插入了：
cur = new Node(kv);
//规则3：不会出现连续的红色
//规则4：每条路径上黑色相同
//宁可去违法3规则也不去违法4规则
cur->_col = RED;
if (parent->_kv.first < kv.first)//插入的值比这个值要大就链接在右边
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//parent是怎么连接的，插入第一个节点不需要考虑parent；
cur->_parent = parent;//三叉链
//红黑树的关键是叔叔（u），u存在且为红，变色继续往上处理，AVL树很严格。稍微改变就得旋转，
//如果u不存在或者u存在且为黑，旋转 + 变色，四转旋转，是单旋还是双旋转）
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
assert(grandfather);
assert(grandfather->_col == BlACK);
//关键是看u
if (parent==grandfather->_left)//如果父亲（p）是祖父（g）的右边，叔叔（u）就是祖父（g）的左边
{
Node* uncle = grandfather->_right;
//情况1：叔叔存在，且叔叔的颜色是红
if (uncle && uncle->_col == RED)
{
//把叔叔和父亲的颜色变黑
parent->_col = uncle->_col = BlACK;
//把祖父变红
grandfather->_col = RED;
//继续往上处理(把祖父当成cur，再去找cur的父亲，更新cur的父亲，再走else)
cur = grandfather;
parent = cur->_parent;
}
//情况2&&情况3:uncle不存在+存在且为黑
else
{
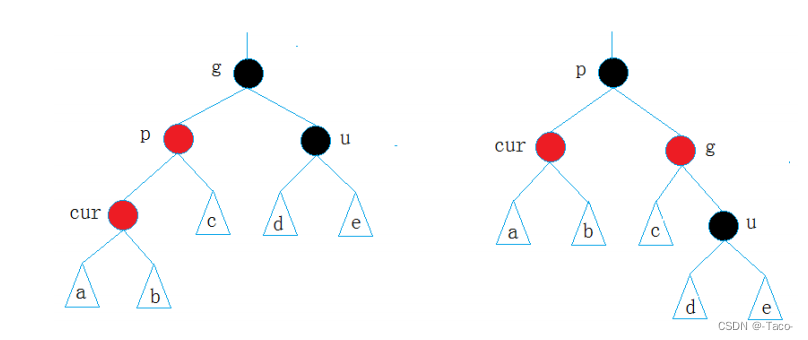
//情况2：右单旋+变色
// g
// p u
//c
if (cur == parent->_left)
{
//单旋+变色
RotateR(grandfather);
parent->_col = BlACK;
grandfather->_col = RED;
}
else
{
//情况3：
// g
// p u
// c
//先以p为轴点左单选
RotateL(parent);
RotateR(grandfather);
cur->_col = BlACK;
grandfather->_col = RED;
}
break;
}
}
else//如果p是g的左，u就是p的右
{
Node* uncle = grandfather->_left;
//情况1：叔叔存在，且叔叔的颜色是红
if (uncle && uncle->_col == RED)
{
//把叔叔和父亲的颜色变黑
parent->_col = uncle->_col = BlACK;
//把祖父变红
grandfather->_col = RED;
//继续往上处理(把祖父当成cur，再去找cur的父亲，更新cur的父亲，再走else)
cur = grandfather;
parent = cur->_parent;
}
//情况2&&情况3:uncle不存在+存在且为黑
else
{
//情况2：
// g
// u p
// c
if (cur == parent->_right)
{
//单旋+变色
RotateL(grandfather);
parent->_col = BlACK;
grandfather->_col = RED;
}
else
{
//情况3：
// g
// u p
// c
//先以p为轴点左单选
RotateR(parent);
RotateL(grandfather);
cur->_col = BlACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BlACK;
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()
{
//代码的枚举已经间接表示出我们创建的树每个结点不是黑就是红色
if (_root == nullptr)
{
return true;
}
if (_root->_col == RED)
{
cout << "根节点不是黑色" << endl;
return false;
}
//上面两种包括不能同时出现两个红色节点，都是十分好判断的,只有每条路径上黑色结点个数相同这个条件比较
//难判断。我们遍历整个树利用前序遍历（深度优先遍历）把整个树遍历一边，注意每当遇见黑结点的时候就+1，
//最后直到空，最后把这些各个路径的值用一个容器存起来，前序利用递归去遍历，如何确保递归到一个根回退
//的时候再回到那个黑结点导致+1重复计算的问题，使用传值去传值，让每个递归函数的栈帧里面的计数值统计就行
//黑色节点数量基准值
int benchmark = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BlACK)
++benchmark;
cur = cur->_left;
}
return PrevCheck(_root, 0,benchmark);
}
private:
bool PrevCheck(Node* root, int blackNum,int benchmark)
{
//如果这里构造一个容器存入所有的值，之后再去遍历一遍，太过于复杂，直接拿最左最右两边，左右两边不用看
//错了还是对了，就算左右两边错了，都不一样树也是错的，这里构造一个基准值去判断
if (root == nullptr)
{
//cout << blackNum << endl;
//return;
if (blackNum != benchmark)
{
cout << "黑色节点的数量不相等" << endl;//这不是一次返回到最外面，这里是递归会层层
//返回到最外面
return false;
}
else
{
return true;
}
}
if (root->_col == BlACK)
{
++blackNum;
}
//上面是解决了计算不同路径黑色结点数量是否相同，下面是检查是否是会出现连续的红色结点，但是如果去找
//这个结点的子结点，它有左孩子有右孩子，有可能都有，有可能都没有，或者只有一个，情况比较复杂
//所以我们就去找它的父结点，因为这个前序遍历反正会把树遍历一遍，比较它的父亲更方便只需要看一次即可；
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "存在连续的红色节点" << endl;
return false;
}
return PrevCheck(root->_right,blackNum,benchmark) &&
PrevCheck(root->_right, blackNum, benchmark);
}
void RotateR(Node* parent)//右旋
{
//右旋前
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
//开始旋转
Node* ppNode = parent->_parent;//先保存一下之前parent的parent，之后用来连接旋转后的subL
//但是不知道这之前parent的ppnode，我们下面的树是它的左树还是右树，就得分情况讨论
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
//说明_root要变成subL
_root = subL;
subL->_parent = nullptr;//不置空就会局部形成环状结构
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
void RotateL(Node* parent)//左旋
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//注意顺序；
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
//subRL->_parent = parent;
//a,b,c都是高度为L的树，但是L可以=0
//c的L之前分析过不会为0，如果L=0的话
//这里subRL就发生了空指针解引用的问题
//这里记录一下ppNode：
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
//还差subR的父亲；（这里有两种情况，parent是根）
//parent是子树的根
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;//根是没有父亲的
}
else//子树的情况，上面还有个节点，假设为ppNode
{
//之前是parent的parent的ppNode，但是现在parent的parent是subR
//所以就需要一个值记录之前，没改节点之前的parent的parent，之后在用现在的subR去连接它
//但是是ppNode的左还是右还是不清楚；还得讨论
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
void TestRedBlackTree1()
{
int a[] = { 16,3,7,11,9,26,18,14,15 };
RedBlackTree<int, int>t1;
for (auto e : a)
{
t1.Insert(make_pair(e, e));
}
t1.InOrder();
cout << "Isbalance:" << t1.IsBalance() << endl;
}
这里的旋转直接复用了上面AVL树的左旋和右旋，只是缺少了平衡因子的重置，增添了新的变色
上面红黑树（插入）我们已经基本剖析完了，下面我们用我们的红黑树，去封装一下map和set，
库里面我们可以看出来它只封装了一颗树就同时完成了map和set，我们知道map和set一个是kv模型一个是k模型，它是怎么封装一次完成两个的？
map
set
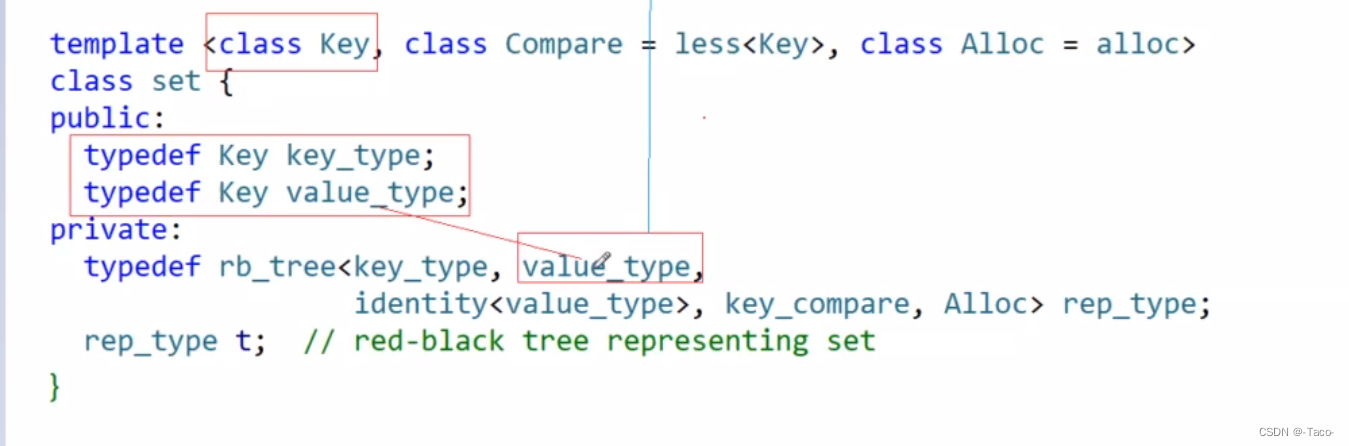
看起来是kv，但是v这里也传的是k
map
对于map来说，key_type是key，value_type是value_type的pair
所以这个树它也不知道它是map还是set，做了一个模板，如果要set就传key，key，如果要map就传key，pair;用了一颗泛型结构的RBtree，通过不同的实例化参数，实现了map和set；
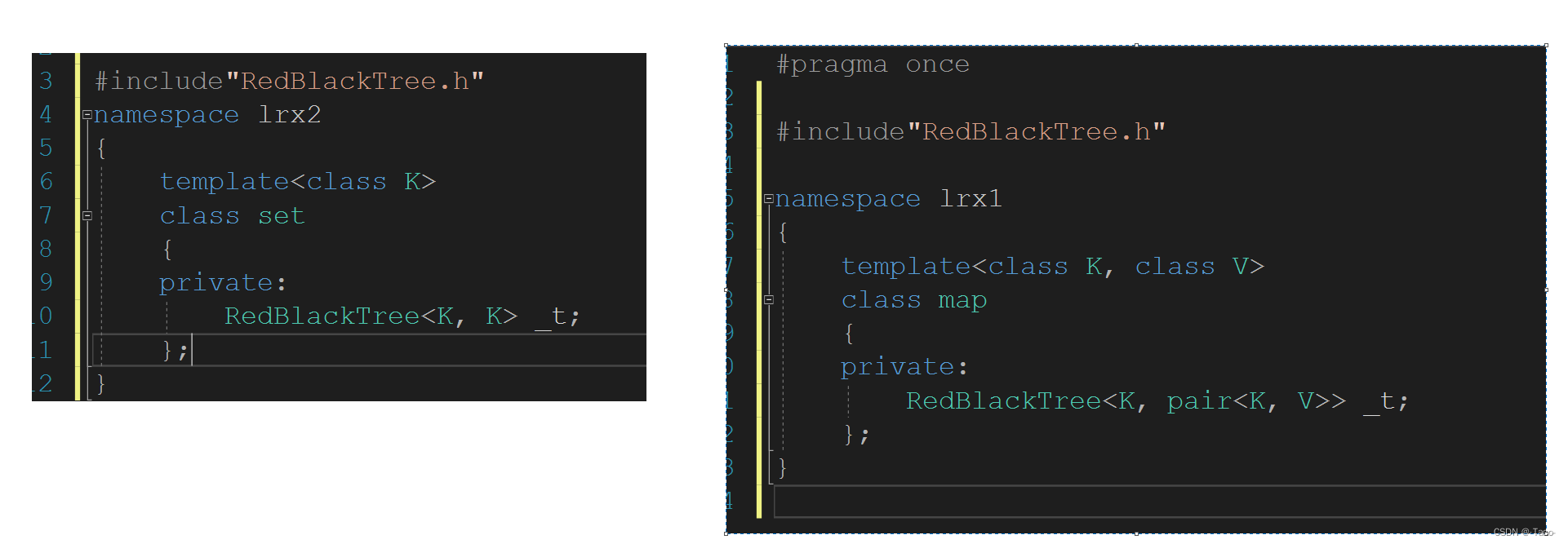
这么设计我们发现是不是可以不需要第一个参数都是K，只有第二个才有区别，其实第一个的传值不能被省略，红黑树的功能不止有insert，还有find，find如果是map不是拿pair去查找，而是用的value，所以都得留；
但是这么设计又出现了一个问题，我们在插入的时候的那个比较（二叉树的插入）我们之前是用的pair 的first比较的，但是这里我们不能拿data去直接比较
如果拿data去比较，这时传的是KV，V是pair，pair我们之前的逻辑是pair的first，但是这里的泛型编程也不能去写我们插入data值的first因为如果data这时候传入的是key值它没有first，前后相互矛盾了，库里面是这么做的，传入了一个class keyofvalue这个参数去判断，如果存入的是set这里只需要比较key的值就行，如果是存入的是map这里就去比较value的first
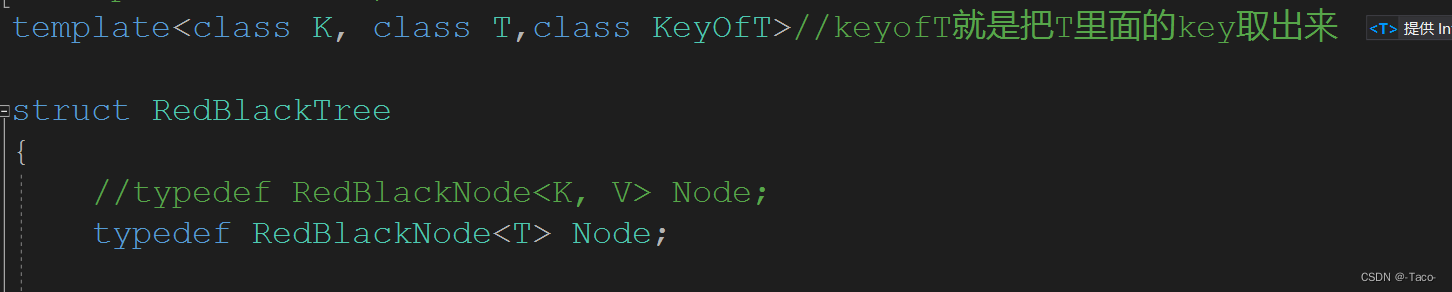
这里通过多传一个参数，之后分别在map和set里面去实现（利用仿函数）
库里对红黑树的实现采用了之前类似链表地方的写法，使用了一个header 的头节点作为哨兵位来找头找尾，我们在自己实现的时候采取另外一种方式；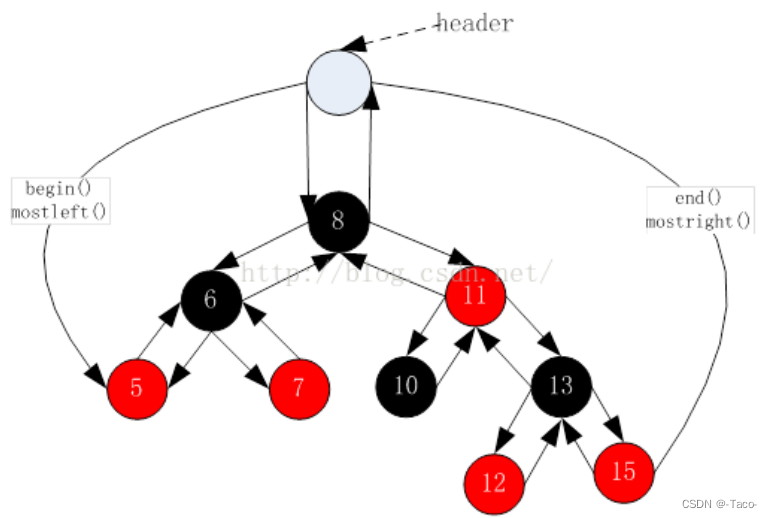
map和set的迭代器都是使用了红黑树的迭代器，所以本质上我们只需要写红黑树的迭代器就可以;
map和set就没有什么东西，都是下层对红黑树的封装
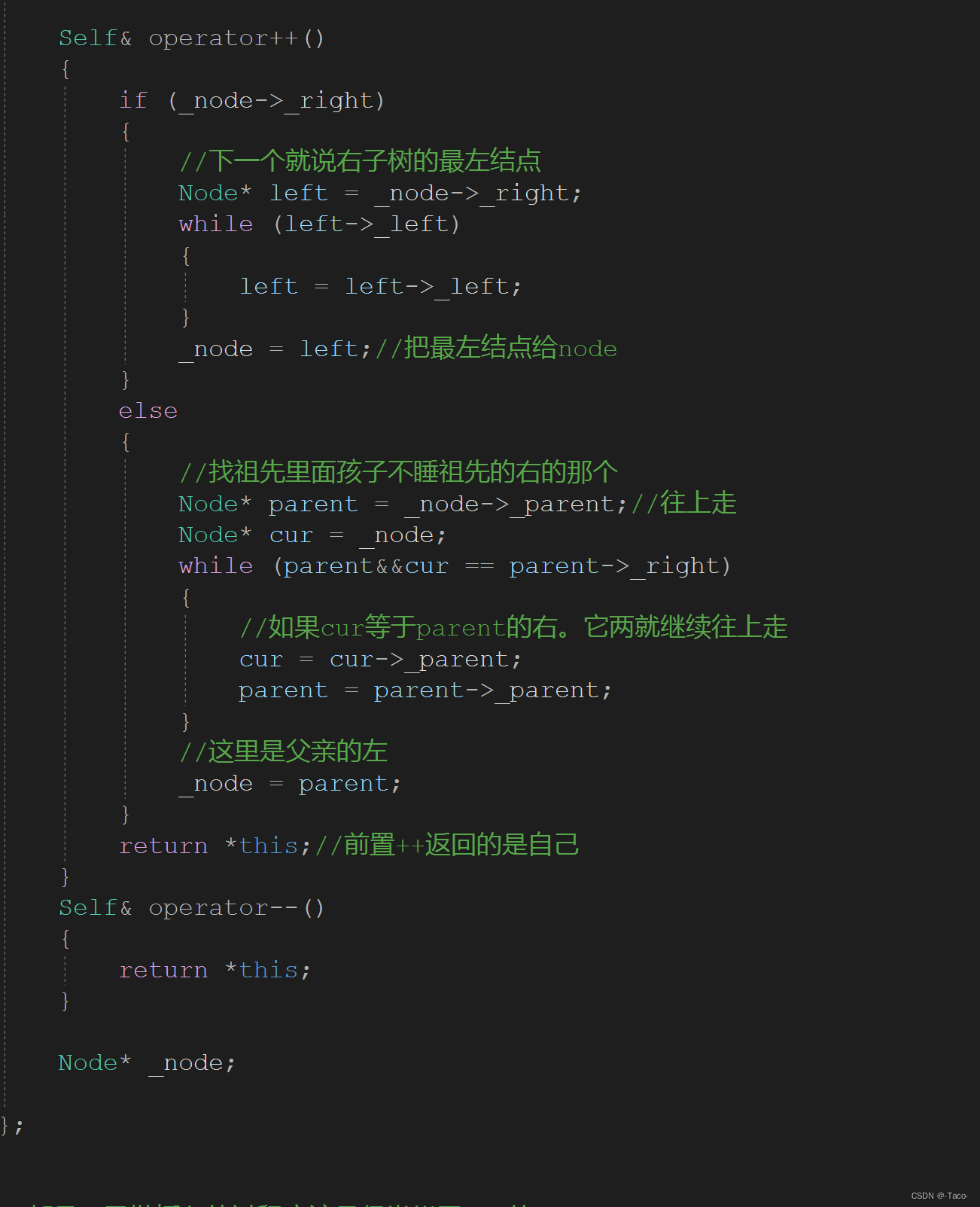
迭代器++的思路
--反着走就行
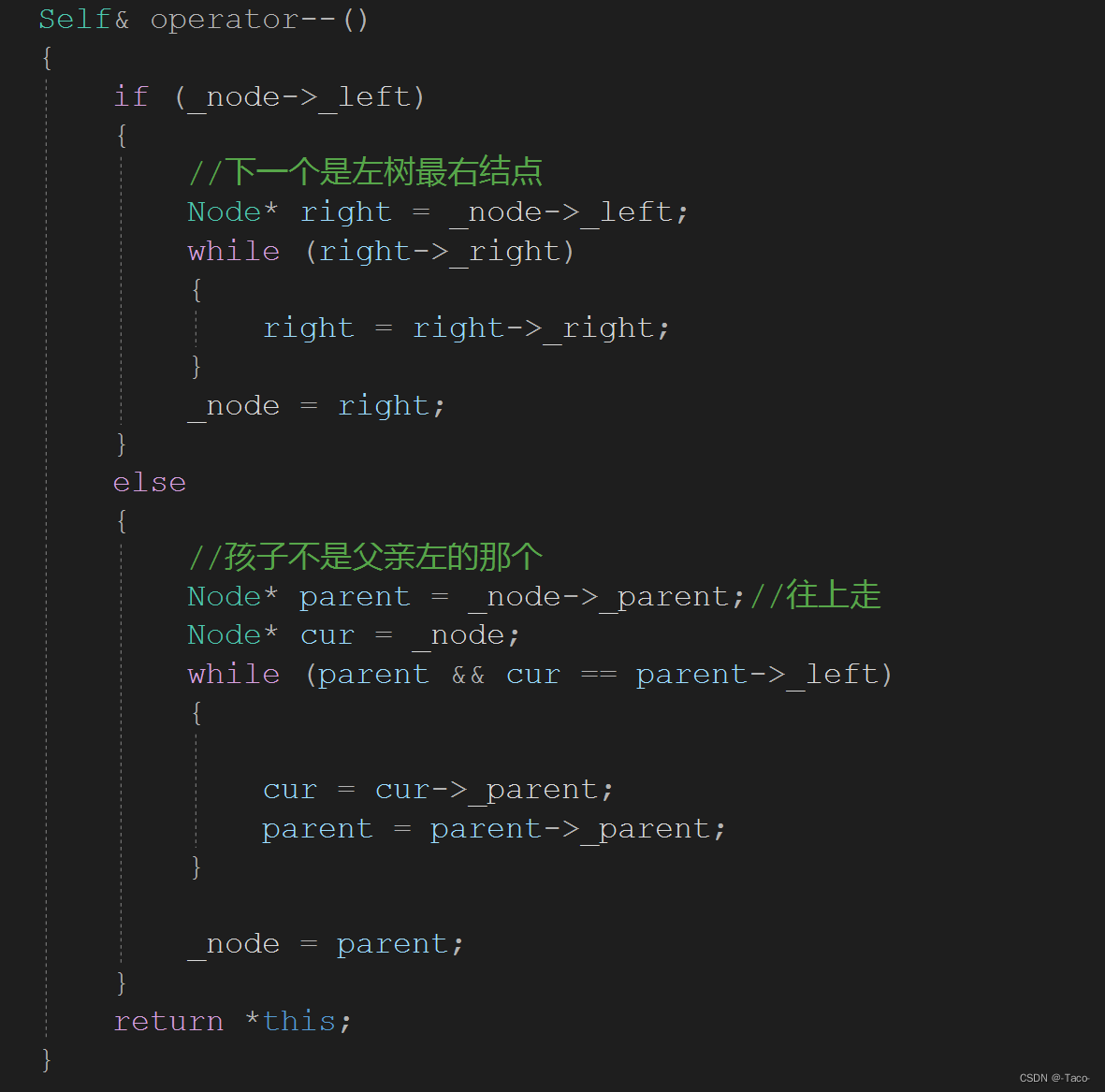
删除这里跟avl树一样不写，过于复杂，不需要掌握；
完整版的红黑树代码：
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;
enum Colour
{
RED,
BlACK
};
//template<class K,class V>
template<class T>
struct RedBlackNode
{
//这个跟AVL的结点设计差不多，都需要三叉链
RedBlackNode<T>* _left;
RedBlackNode<T>* _right;
RedBlackNode<T>* _parent;
//pair<K, V> _kv;
T _data;
Colour _col;
//RedBlackNode(const pair<K, V>& kv)
RedBlackNode(const T& data)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _data(data)
{}
};
template<class T, class Ref, class Ptr>//Ref代表引用类型，Ptr代表指针类型
struct __RedBlackTreeIterator
{
typedef RedBlackNode<T> Node;
typedef __RedBlackTreeIterator<T, Ref, Ptr>Self;
__RedBlackTreeIterator(Node* node)
:_node(node)
{}
Ref operator*()
{
return _node->_data;//对于set是个key对于map是first，我们也不知得，所以采取了泛型编程
}
Ptr operator->()
{
return &_node->_data;//对于set返回的就是key*，map就是pair*
}
bool operator!=(const Self& s)const
{
return _node != s._node;//用结点的指针去比较
}
bool operator==(const Self& s)const
{
return _node == s._node;
}
Self& operator++()
{
if (_node->_right)
{
//下一个就说右子树的最左结点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left;//把最左结点给node
}
else
{
//找祖先里面孩子不睡祖先的右的那个
Node* parent = _node->_parent;//往上走
Node* cur = _node;
while (parent&&cur == parent->_right)
{
//如果cur等于parent的右。它两就继续往上走
cur = cur->_parent;
parent = parent->_parent;
}
//这里是父亲的左
_node = parent;
}
return *this;//前置++返回的是自己
}
Self& operator--()
{
if (_node->_left)
{
//下一个是左树最右结点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right;
}
else
{
//孩子不是父亲左的那个
Node* parent = _node->_parent;//往上走
Node* cur = _node;
while (parent && cur == parent->_left)
{
cur = cur->_parent;
parent = parent->_parent;
}
_node = parent;
}
return *this;
}
Node* _node;
};
//都是三叉链插入的过程应该是很类似于AVL的
//template<class K, class V>
template<class K, class T, class KeyOfT>//keyofT就是把T里面的key取出来
struct RedBlackTree
{
//typedef RedBlackNode<K, V> Node;
typedef RedBlackNode<T> Node;
public:
typedef __RedBlackTreeIterator<T, T&, T*> iterator;
//这是一个迭代器类型定义，用于遍历红黑树中的元素。其中，T表示节点中存储的数据类型，T& 表示迭代器返回
//的引用类型，T* 表示迭代器返回的指针类型。这个迭代器类型定义是基于三叉链的红黑树实现的，它包含了一个
//指向节点的指针，可以通过重载运算符实现迭代器的自增、自减、解引用等操作。
iterator begin()
{
Node* left = _root;//找最左结点
while (left && left->_left)
{
left = left->_left;
}
return iterator(left);//在这里使用一个构造，构造一个最左结点的迭代器然后返回
}
iterator end()
{
return iterator(nullptr);
}
//先插入之后再平衡
//写的时候能用非递归就尽量用非递归；
//bool Insert(const pair<K, V>& kv)//插入的时候本质上还是跟搜索树是一样的；(大就往右走，小就往左走）
//bool Insert(const T& data)为了构造operator[]改造一下
pair<iterator,bool> Insert(const T& data)
{
KeyOfT kot;//创建一个仿函数的对象
if (_root == nullptr)
{
//_root = new Node(kv);
_root = new Node(data);
_root->_col = BlACK;
//return true;
return make_pair(iterator(_root), true);
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)//让cur走到空的位置，parent指向cur
{
//if(cur->_kv.first<kv.first)
if (kot(cur->_data) < kot(data))//插入的值比这个大走右边
{
parent = cur;
cur = cur->_right;
}
//else if (cur->_kv.first > kv.first)//插入的值比要比较的值小，就走左边
else if (kot(cur->_data) > kot(data))
{
parent = cur;
cur = cur->_left;
}
else
{
//return false;
return make_pair(iterator(cur), false);
}
}
//这里就该插入了：
cur = new Node(data);
Node* newnode = cur;
//规则3：不会出现连续的红色
//规则4：每条路径上黑色相同
//宁可去违法3规则也不去违法4规则
cur->_col = RED;
//if (parent->_kv.first < kv.first)//插入的值比这个值要大就链接在右边
if (kot(parent->_data) < kot(data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//parent是怎么连接的，插入第一个节点不需要考虑parent；
cur->_parent = parent;//三叉链
//红黑树的关键是叔叔（u），u存在且为红，变色继续往上处理，AVL树很严格。稍微改变就得旋转，
//如果u不存在或者u存在且为黑，旋转 + 变色，四转旋转，是单旋还是双旋转）
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
assert(grandfather);
assert(grandfather->_col == BlACK);
//关键是看u
if (parent == grandfather->_left)//如果父亲（p）是祖父（g）的右边，叔叔（u）就是祖父（g）的左边
{
Node* uncle = grandfather->_right;
//情况1：叔叔存在，且叔叔的颜色是红
if (uncle && uncle->_col == RED)
{
//把叔叔和父亲的颜色变黑
parent->_col = uncle->_col = BlACK;
//把祖父变红
grandfather->_col = RED;
//继续往上处理(把祖父当成cur，再去找cur的父亲，更新cur的父亲，再走else)
cur = grandfather;
parent = cur->_parent;
}
//情况2&&情况3:uncle不存在+存在且为黑
else
{
//情况2：右单旋+变色
// g
// p u
//c
if (cur == parent->_left)
{
//单旋+变色
RotateR(grandfather);
parent->_col = BlACK;
grandfather->_col = RED;
}
else
{
//情况3：
// g
// p u
// c
//先以p为轴点左单选
RotateL(parent);
RotateR(grandfather);
cur->_col = BlACK;
grandfather->_col = RED;
}
break;
}
}
else//如果p是g的左，u就是p的右
{
Node* uncle = grandfather->_left;
//情况1：叔叔存在，且叔叔的颜色是红
if (uncle && uncle->_col == RED)
{
//把叔叔和父亲的颜色变黑
parent->_col = uncle->_col = BlACK;
//把祖父变红
grandfather->_col = RED;
//继续往上处理(把祖父当成cur，再去找cur的父亲，更新cur的父亲，再走else)
cur = grandfather;
parent = cur->_parent;
}
//情况2&&情况3:uncle不存在+存在且为黑
else
{
//情况2：
// g
// u p
// c
if (cur == parent->_right)
{
//单旋+变色
RotateL(grandfather);
parent->_col = BlACK;
grandfather->_col = RED;
}
else
{
//情况3：
// g
// u p
// c
//先以p为轴点左单选
RotateR(parent);
RotateL(grandfather);
cur->_col = BlACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BlACK;
//return true;
return make_pair(iterator(newnode),true);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool IsBalance()
{
//代码的枚举已经间接表示出我们创建的树每个结点不是黑就是红色
if (_root == nullptr)
{
return true;
}
if (_root->_col == RED)
{
cout << "根节点不是黑色" << endl;
return false;
}
//上面两种包括不能同时出现两个红色节点，都是十分好判断的,只有每条路径上黑色结点个数相同这个条件比较
//难判断。我们遍历整个树利用前序遍历（深度优先遍历）把整个树遍历一边，注意每当遇见黑结点的时候就+1，
//最后直到空，最后把这些各个路径的值用一个容器存起来，前序利用递归去遍历，如何确保递归到一个根回退
//的时候再回到那个黑结点导致+1重复计算的问题，使用传值去传值，让每个递归函数的栈帧里面的计数值统计就行
//黑色节点数量基准值
int benchmark = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BlACK)
++benchmark;
cur = cur->_left;
}
return PrevCheck(_root, 0, benchmark);
}
private:
bool PrevCheck(Node* root, int blackNum, int benchmark)
{
//如果这里构造一个容器存入所有的值，之后再去遍历一遍，太过于复杂，直接拿最左最右两边，左右两边不用看
//错了还是对了，就算左右两边错了，都不一样树也是错的，这里构造一个基准值去判断
if (root == nullptr)
{
//cout << blackNum << endl;
//return;
if (blackNum != benchmark)
{
cout << "黑色节点的数量不相等" << endl;//这不是一次返回到最外面，这里是递归会层层
//返回到最外面
return false;
}
else
{
return true;
}
}
if (root->_col == BlACK)
{
++blackNum;
}
//上面是解决了计算不同路径黑色结点数量是否相同，下面是检查是否是会出现连续的红色结点，但是如果去找
//这个结点的子结点，它有左孩子有右孩子，有可能都有，有可能都没有，或者只有一个，情况比较复杂
//所以我们就去找它的父结点，因为这个前序遍历反正会把树遍历一遍，比较它的父亲更方便只需要看一次即可；
if (root->_col == RED && root->_parent->_col == RED)
{
cout << "存在连续的红色节点" << endl;
return false;
}
return PrevCheck(root->_right, blackNum, benchmark) &&
PrevCheck(root->_right, blackNum, benchmark);
}
void RotateR(Node* parent)//右旋
{
//右旋前
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
//开始旋转
Node* ppNode = parent->_parent;//先保存一下之前parent的parent，之后用来连接旋转后的subL
//但是不知道这之前parent的ppnode，我们下面的树是它的左树还是右树，就得分情况讨论
subL->_right = parent;
parent->_parent = subL;
if (_root == parent)
{
//说明_root要变成subL
_root = subL;
subL->_parent = nullptr;//不置空就会局部形成环状结构
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
}
void RotateL(Node* parent)//左旋
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
//注意顺序；
parent->_right = subRL;
if (subRL)
{
subRL->_parent = parent;
}
//subRL->_parent = parent;
//a,b,c都是高度为L的树，但是L可以=0
//c的L之前分析过不会为0，如果L=0的话
//这里subRL就发生了空指针解引用的问题
//这里记录一下ppNode：
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
//还差subR的父亲；（这里有两种情况，parent是根）
//parent是子树的根
if (_root == parent)
{
_root = subR;
subR->_parent = nullptr;//根是没有父亲的
}
else//子树的情况，上面还有个节点，假设为ppNode
{
//之前是parent的parent的ppNode，但是现在parent的parent是subR
//所以就需要一个值记录之前，没改节点之前的parent的parent，之后在用现在的subR去连接它
//但是是ppNode的左还是右还是不清楚；还得讨论
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};
//void TestRedBlackTree1()
//{
// int a[] = { 16,3,7,11,9,26,18,14,15 };
// RedBlackTree<int, int>t1;
// for (auto e : a)
// {
// t1.Insert(make_pair(e, e));
// }
// t1.InOrder();
// cout << "Isbalance:" << t1.IsBalance() << endl;
//
//
//}
map
#pragma once
#include"RedBlackTree.h"
namespace lrx1
{
template<class K, class V>
class map
{
struct MapKeyOfT
{
const K& operator()(const pair<K,V>&kv)
{
return kv.first;
}
};
public:
//typedef RedBlackTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;
//凡是要取一个类模板里面的类型，如果是普通类里面的类型直接取就行，凡是要去typedef，或者用这个类型
//去定义取一个类模板里面再定义的类型，就要加一个typename，“RedBlackTree<K, pair<K, V>,
//MapKeyOfT>”这是一个类模板，要在类模板里面取一个相关的类型，内嵌定义的类型，在它里面typedef或者
//内部类也是这么取的，静态变量也是这么取的，这时编译器就不知得它是变量还是类型，所以就得加一个
//typename，这会编译器也不敢去分，因为这会模板还没开始实例化，所以加typename告诉编译器这是个类型
//不是一个静态变量，等实例化以后再去取
typedef typename RedBlackTree<K, pair<K, V>, MapKeyOfT>::iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
//bool insert(const pair<K,V>& kv)
pair<iterator,bool> insert(const pair<K, V>& kv)
{
return _t.Insert(kv);
}
V& operator[](const K& key)//[]只用在map，所以不能在红黑树内里写，在这里表示出来即可;
{
pair<iterator, bool>ret = insert(make_pair(key,V()));//V给的缺省值，如果是int就是0
//指针就是空指针，如果是string就调用string的默认构造，
return ret.first->second;
}
private:
RedBlackTree<K, pair<K, V>,MapKeyOfT> _t;
};
void test_map()
{
/*map<int,int>m;
m.insert(make_pair(1,2));
m.insert(make_pair(5,2));
m.insert(make_pair(2,2));*/
string arr[] = { "苹果","西瓜","苹果","西瓜","苹果","西瓜","苹果","香蕉","苹果" };
map<string, int>countMap;
for (auto& str : arr)
{
countMap[str]++;
}
map<string, int>::iterator it = countMap.begin();
while (it != countMap.end())
{
cout << it->first << ":" << it->second << endl;
++it;
}
//支持了迭代器也就支持范围for
}
}
set
#pragma once
#include"RedBlackTree.h"
namespace lrx2
{
template<class K>
class set
{
struct SetKeyOfT
{
const K & operator()(const K& key)
{
return key;
}
};
public:
typedef typename RedBlackTree<K,K,SetKeyOfT>::iterator iterator;
iterator begin()
{
return _t.begin();
}
iterator end()
{
return _t.end();
}
//bool insert(const K &kv)
pair<iterator,bool> insert(const K& kv)
{
return _t.Insert(kv);
}
private:
RedBlackTree<K, K,SetKeyOfT> _t;
};
void test_set()
{
set<int>s;
s.insert(3);
s.insert(2);
s.insert(1);
s.insert(5);
set<int>::iterator it = s.begin();
while (it != s.end())
{
cout << *it << " ";
++it;
}
cout << endl;
}
}红黑树的应用场景大于AVL树；
![从应用层到MCU，看Windows处理键盘输入 [2.a.1.传球手User32.dll]](https://img-blog.csdnimg.cn/e9f9d2588d4b4c46943088b83722e08e.png)