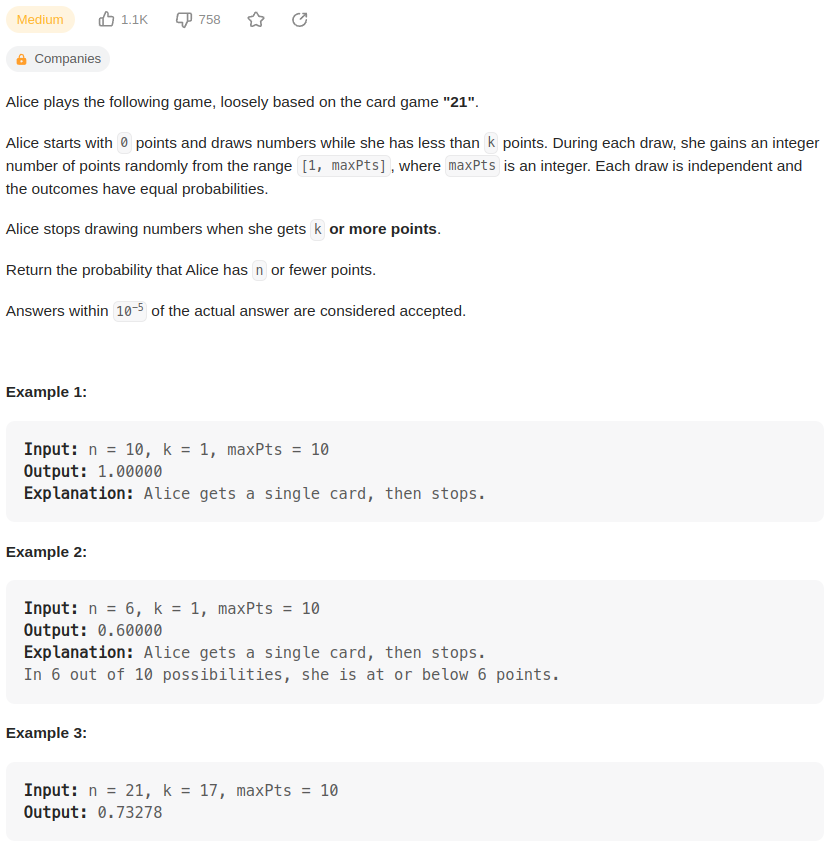
起始点数为0，当手上点数 < k 时抽取新的卡片，
每次抽取的点数范围在 1 ~ maxPts.
每次收取是独立的，每个点数概率相同。
当手上点数 >= k 时游戏结束。

返回手上点数 <= n 的概率。

思路：

先看特殊情况，
k = 0时，不会抽取新的卡片，游戏直接结束，点数 <= n 的概率为1.
手上点数 < k 时会抽新的卡片，直到点数 >= k为止，

那么游戏结束时点数范围在 k ~ k + maxPts - 1.
(假设手上点数在临界的k-1, 最后一次抽到最大点数maxPts).

n如果 < k, 那么最后概率是0，
n > k + maxPts, 那么最后概率是1。

再分析一般情况。

假设最大点数maxPts=3，要找到点数=5的概率。
抽取点数范围在[1, maxPts], 所以可能抽到的是1, 2, 3, 概率都是1/3,

如果手上已有点数为4，则需要再抽取1，概率=prob(4) * 1/3
手上点数为3，则需要再抽取2，概率= prob(3) * 1/3
手上点数为2，则需要再抽取3，概率=prob(2) * 1/3
如果手上点数为1，就没法凑够5了，因为卡片最大点数是3.

从上面的情况可以看出来，想要得到点数k
P(k) = P(k-1) * 1/maxPts + P(k-2) * 1/maxPts + … + P(k-maxPts) * 1/maxPts
这相当于一个 k-1 到 k-maxPts 的一个长度为maxPts的滑动窗口。

假设dp[i] = P(i) (P为概率），sum = dp[i-1] + dp[i-2] + … + dp[i-maxPts]
那么dp[i] = sum / maxPts.
移动 i, 超出滑动窗口左边界的要从sum中减掉，新进入的dp[i]要加到sum里。

i 这里指的是已经得到的点数。
同时，要判断 i < k. 因为 i >= k时游戏结束，游戏结束后把dp[i]加到结果res里。
i >= maxPts时，左边界开始超出滑动窗口，需要把左边的部分从sum中减掉。

public double new21Game(int n, int k, int maxPts) {
    if(k == 0 || n >= k + maxPts) return 1.0;
    double[] dp = new double[n+1];
    double sum = 1.0;
    double res = 0.0;
    dp[0] = 1.0;
    for(int i = 1; i <= n; i++) {
        dp[i] = sum / maxPts;
        if(i < k) sum += dp[i];
        else res += dp[i];
        if(i - maxPts >= 0) sum -= dp[i-maxPts];
    }
    return res;
}