概念

傅里叶变换是一种将一个信号（可以是声音、图像等）从时域（时间轴上）转换到频域（频率轴上）的数学工具。

它可以将一个复杂的信号分解成若干简单的正弦波，每个正弦波都有自己的频率、振幅和相位。这个过程可以被看作是把一个复杂的信号拆分为若干个单频信号的叠加。

通俗地说，可以把傅里叶变换类比成把一张拼图分解成若干个简单的小拼图，每个小拼图都有自己的形状和颜色，然后再把这些小拼图按照一定的比例和顺序拼接起来，就可以得到原来的完整拼图。类似地，傅里叶变换可以把复杂的信号分解成简单的正弦波，并按照一定的比例和顺序组合起来，得到原来的信号。如下图：

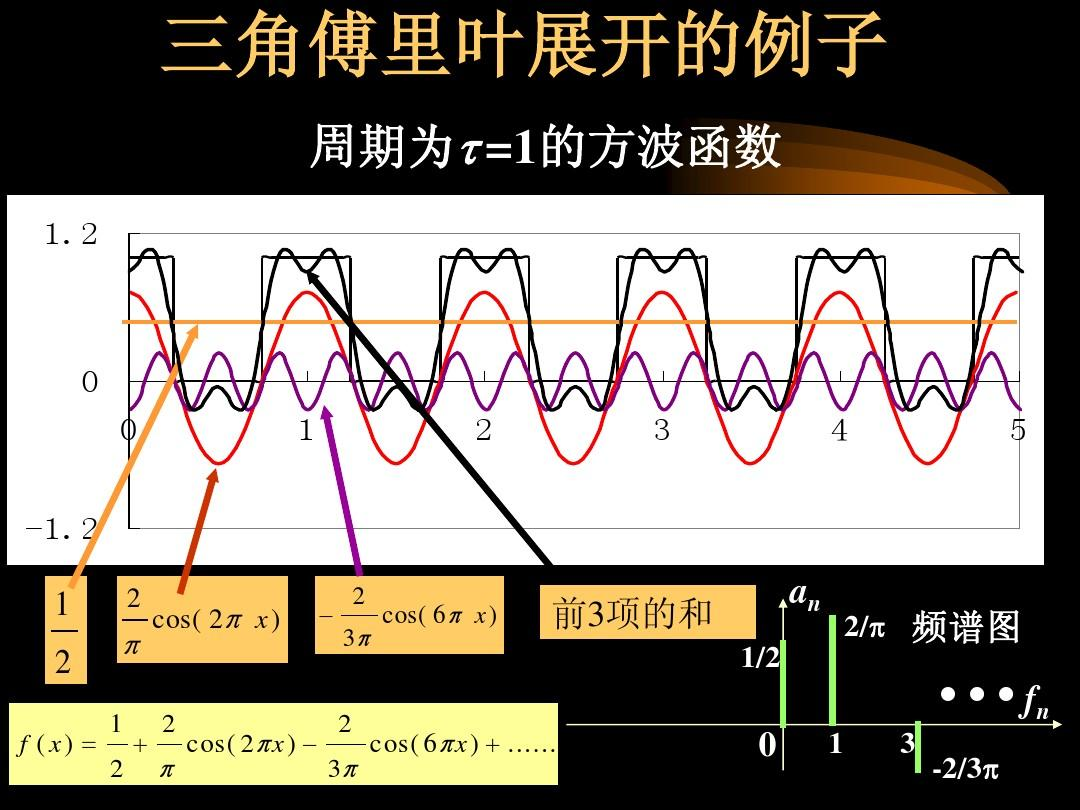
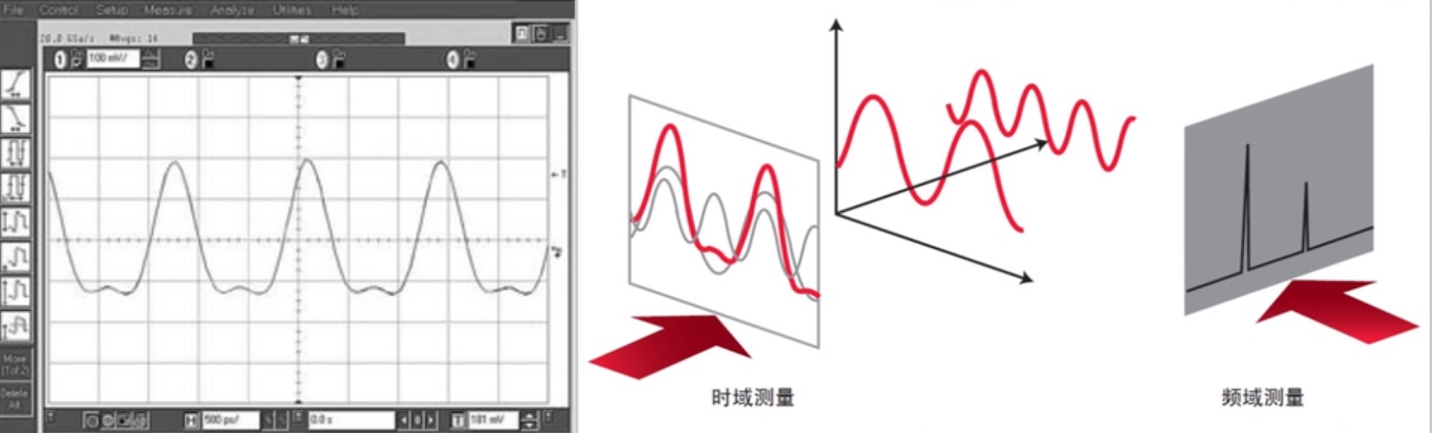
时域和频域的关系

傅里叶变换的分类

傅里叶变换可以分为以下几类：

1. 连续时间傅里叶变换(CTFT): 一般情况下，若“傅里叶变换”一词的前面未加任何限定语，则指的是“连续傅里叶变换”。.连续时间傅里叶变换主要针对连续时间信号，将一个信号从时域(时间轴)转换到频域(频率轴)，用于信号的频率分析和滤波等。

2. 离散时间傅里叶变换(DTFT): 离散时间傅里叶变换主要针对离散时间信号，也是将一个时域信号转换到频域，并且可以得到长度为无限的频域序列。