红黑树封装set和map(插入部分）

news2025/1/11 0:07:35

文章目录

  • 前言
  • 1.设计大致思路
  • 2.改造封装红黑树
    • 1.插入节点
    • 2.迭代器的实现
  • 3.map和set的封装
    • 1.代码实现
    • 2.简单测试

前言

之前我们实现了红黑树的插入的部分，本文主要介绍将之前实现的红黑树封装成map和set。我们是以学习的角度来封装容器，不用非要把库中容器所有功能都实现出来。我们主要目的是学习库中代码设计技巧和模板复用的思想。

1.设计大致思路

我们在实现之前还是和以前一样去看看库中是怎么实现的。这里先简单介绍一下库中容器实现的思路。库中设计的大概思路是：将红黑树设计一个类模板，我们map和set直接复用一颗红黑树，将红黑树的接口进行封装形成自己的接口。这样相当于map和set是都是复用一份代码，我们只用维护好红黑树的代码就可以实现出相关容器了。

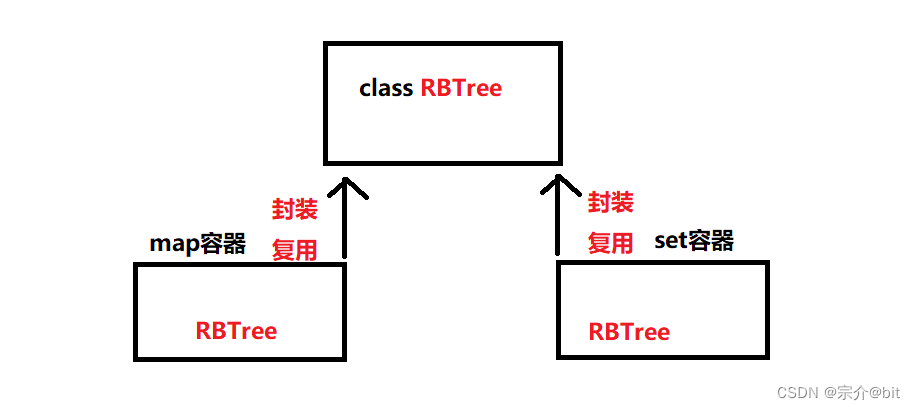
在这里插入图片描述

那我们来思考一下，这个map和set最大的区别就是存储的节点。set只是存储的单一key值，而存储的是key-val键值对。因此我们知道就必须有个模板参数控制红黑树节点是存储的什么值。同时我们因为我们find和erase这些接口需要知道这个key的类型，因此还要单独有个模板参数的来标识key。

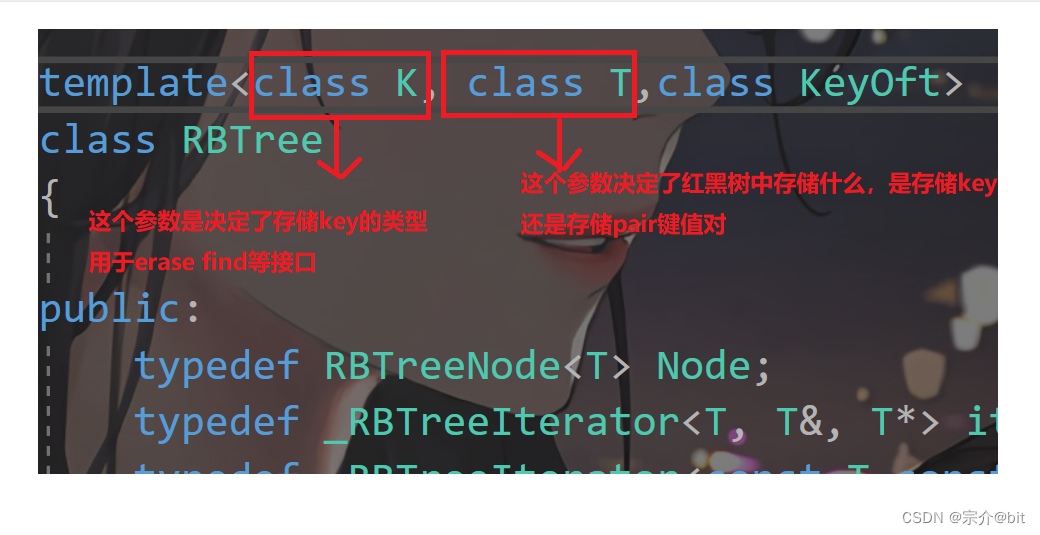
在这里插入图片描述

同时对于存储的节点值不确定，我们需要在进行节点key值比较的时候可以定义出仿函数用于控制比较逻辑，我们用什么值来进行比较。也就是说第三个keyOft,是用来控制比较逻辑的，在map和set中进行封装的时候传入对应的仿函数即可。

有了这个思路后，我们将之前的红黑树改成一个类模板。

2.改造封装红黑树

我们将之前的写好的红黑拿过来改造，旋转变色调整逻辑我们不用改动，我们唯一要改动的就是这个插入逻辑，我们先将红黑树的大体框架拿过来。

节点构建

enum Colour
{
	RED,
	BLACK,
};

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	T _data;
	Colour _col;

	RBTreeNode(const T& data)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _data(data)
		, _col(RED)
	{}
};

template<class K, class T,class KeyOft>
class RBTree
{
public:
typedef RBTreeNode<T> Node;
	Node* Find(const T& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)
			{
				cur = cur->_right;
			}
			else if (cur->_kv.first > key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}

	void InOrder()
	{
		_InOrder(_root);
	}

	bool IsBalance()
	{
		if (_root && _root->_col == RED)
		{
			cout << "根节点颜色是红色" << endl;
			return false;
		}

		int benchmark = 0;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
			{
				++benchmark;
			}
			cur = cur->_left;
		}


		return _Check(_root, 0, benchmark);
	}

	int Height()
	{
		return _Height(_root);
	}

private:
	void _Destroy(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_Destroy(root->_left);
		_Destroy(root->_right);
		delete root;
	}

	int _Height(Node* root)
	{
		if (root == NULL)
			return 0;

		int leftH = _Height(root->_left);
		int rightH = _Height(root->_right);

		return leftH > rightH ? leftH + 1 : rightH + 1;
	}

	bool _Check(Node* root, int blackNum, int benchmark)
	{
		if (root == nullptr)
		{
			if (benchmark != blackNum)
			{
				cout << "某条路径黑色节点的数量不相等" << endl;
				return false;
			}

			return true;
		}

		if (root->_col == BLACK)
		{
			++blackNum;
		}

		if (root->_col == RED
			&& root->_parent
			&& root->_parent->_col == RED)
		{
			cout << "存在连续的红色节点" << endl;
			return false;
		}

		return _Check(root->_left, blackNum, benchmark)
			&& _Check(root->_right, blackNum, benchmark);
	}

	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_kv.first << " ";
		_InOrder(root->_right);
	}

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
		{
			subRL->_parent = parent;
		}

		Node* ppnode = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;

		if (ppnode == nullptr)
		{
			_root = subR;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subR;
			}
			else
			{
				ppnode->_right = subR;
			}

			subR->_parent = ppnode;
		}
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		Node* ppnode = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (parent == _root)
		{
			_root = subL;
			_root->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subL;
			}
			else
			{
				ppnode->_right = subL;
			}
			subL->_parent = ppnode;
		}
	}

private:
	Node* _root = nullptr;
};

上述代码除了添加了3个模板参数其余的都没有改动，这样就是有了个大概的框架。我们接着就是实现插入逻辑和迭代器了。

1.插入节点

这里节点存储什么值，就是插入什么值。节点存储的值是由这个第二个模板参数决定的。这个插入节函数的参数就确定好了，const T&data。这个插入节点返回值我们去看看库中的实现。

在这里插入图片描述

这里返回值是一个pair，这个pair里面存储的是对应位置的节点的迭代器和插入情况。bool值表示是否插入成功，如果已经存在相等的key返回的迭代器就是指向这个key的迭代器,如果插入成功返回的迭代器就是指向这个新插入的节点。

pair< iterator, bool> Insert(const T& data)
	  { 
		 KeyOft kot;
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(iterator(_root), true);
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (kot(cur->_data) < kot(data))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
			   return make_pair(iterator(cur), false);
			}
		}

		cur = new Node(data);
		Node* newnode = cur;
		if (kot(parent->_data) > kot(data))
		{
			parent->_left = cur;
		}
		else
		{
			parent->_right = cur;
		}
		cur->_parent = parent;

		while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;
					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{

					if (cur == parent->_left)
					{
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
			else // (grandfather->_right == parent)
			{

				Node* uncle = grandfather->_left;
				// 情况1：u存在且为红，变色处理，并继续往上处理
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;

					// 继续往上调整
					cur = grandfather;
					parent = cur->_parent;
				}
				else
				{

					if (cur == parent->_right)
					{
						RotateL(grandfather);
						grandfather->_col = RED;
						parent->_col = BLACK;
					}
					else
					{

						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}

					break;
				}
			}
		}

		_root->_col = BLACK;
		return make_pair(iterator(newnode), true);
	}

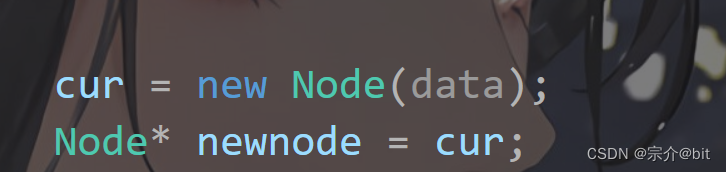
在这里插入图片描述
在这里插入图片描述

这个唯一不同的就是把这个newnode提前保存一下，因为这个节点可能会被调整，保存后通过这个节点构造一个匿名对象迭代器插入到pair中并且返回。这里迭代器并没有实现出来，我们先这样写，之后再实现出迭代器即可。这里返回bool值是为了更清楚知道插入节点的情况。

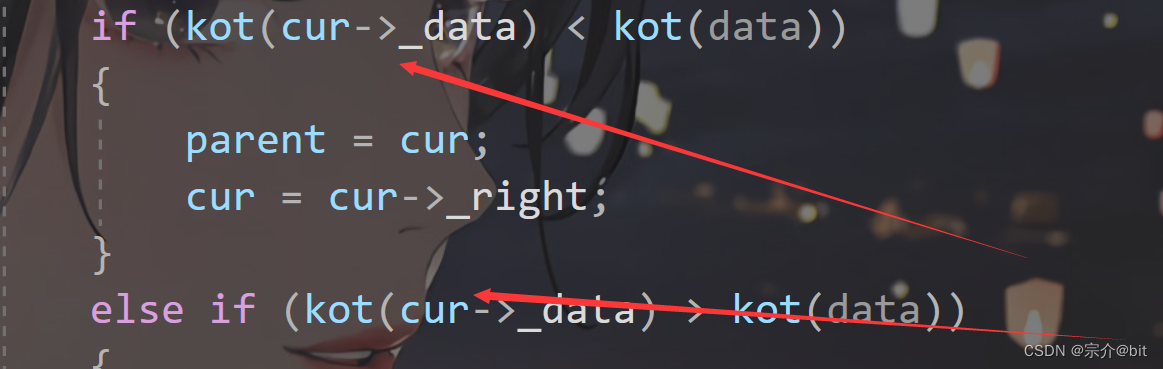
在这里插入图片描述
在这里插入图片描述

这里还需要注意的情况就是这个第三个模板参数，这个第三模板参数是用来控制比较逻辑的，其实就是重载这个()这个运算符，在通过对应的对象来控制这个比较逻辑。因此凡是比较的地方我们通过第三个参数来加以控制。

2.迭代器的实现

迭代器的实现结合我们之前实现链表的迭代器也是采用实现迭代器类模板这种方式来解决。我们的const迭代器和普通迭代器都可以复用这一套模板。结合之前的经验，我们还是采用节点指针来模拟原生指针的行为，我们需要3个模板参数，一个参数用来确定节点中存储值的类型，一个参数是为了模拟原生指针->的操作，作为重载->的返回值,还有一个参数是用来模拟&原生指针的操作，作为操作&的返回值。因为我们想让const迭代器也复用这段代码，所以采用模板实现。

template<class T,class Ref,class Ptr>
struct _RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef _RBTreeIterator<T, Ref, Ptr> Self;
	Node* _node;
	_RBTreeIterator(Node* node)
		:_node(node)
	{}
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator->()
	{
		return &_node->_data;
	}
	bool operator!=(const Self& s )
	{
		return _node != s._node;
	}
	Self& operator++()
	{
		if (_node->_right)
		{
			Node* subRight = _node->_right;
			//右子树中的最左节点
			while (subRight->_left)
			{
				subRight=subRight->_left;
			}
			_node = subRight;
		}
		else
		{
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent&& parent->_right == cur)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}
	Self& operator--()
	{
		if (_node->_left)
		{
			Node* subLeft  = _node->_left;
			//左子树中的最右节点
			while (subLeft->_right)
			{
				subLeft = subLeft->_right;
			}
			_node = subLeft;
		}
		else
		{
			Node* cur = _node;
			Node* parent = _node->_parent;
			while (parent&& parent->_left = cur)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}


};

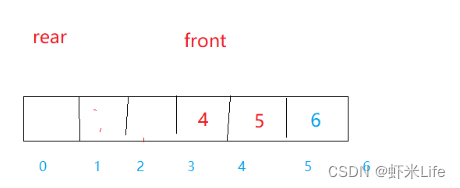
这里->和*以及&没啥好说的，重点在于这个前置++和前置--的操作.关于这个++和–我们还是需要上图来分析一下。

在这里插入图片描述

这里++操作需要结合图去看，将图看懂了代码就很明了。这个++it还是根据这个二叉搜索树的特性来确定这个节点指针的移动方向的。

在这里插入图片描述

这个–操作和++操作其实刚好是对称的，对于这个节点移动我们可以先将最好分析的先分析出来，在结合图去移动指针。比如这个it指向的节点有左子树，这就是最好分析一种情况。

在这里插入图片描述

这个迭代器类实现好以后，我们在红黑树的模板类中申明重命名一下这个迭代器类型。

iterator begin()
	{
		Node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}

		return iterator(cur);
	}

	iterator end()
	{
		return iterator(nullptr);
	}
	const_iterator begin() const
	{
		Node* cur = _root;
		while (cur && cur->_left)
		{
			cur = cur->_left;
		}
		return const_iterator(cur);
	}

	const_iterator end() const
	{
		return const_iterator(nullptr);
	}

然后我们实现一下对应的迭代器接口即可。这个begin是指向红黑树中最小的元素的，也就是红黑树左子树中最左节点。找到这个节点后将其构造对应的迭代器返回即可。这个end接口，我们将其设置为空就行了，通过空指针来构造对应的迭代器。这样的话，我们就将红黑树的类模板给实现好了，map和set直接进行简单的封装复用即可。

3.map和set的封装

1.代码实现

这里map和set的封装其实就是复用一下红黑树这个类模板，让这个类模板实例化出对应的容器

template<class K,class V>
class Map
{
	
public:
	struct MapKeyOft
	{
		const K &operator()(const pair<K,V>&kv)
		{
			return kv.first;
		}
	};
public:
	typedef typename RBTree<K, pair<const K, V>, MapKeyOft>::iterator iterator;
	iterator begin()
	{
		return _t.begin();
	}

	iterator end()
	{
		return _t.end();
	}

	V& operator[](const K& key)
	{
		pair<iterator, bool> ret = _t.Insert(make_pair(key, V()));
		return ret.first->second;
	}

	pair<iterator, bool> insert(const pair<const K, V>& kv)
	{
		return _t.Insert(kv);
	}
	
private:
	RBTree<K, pair<const K, V>, MapKeyOft> _t;

};

map的话直接复用红黑树的接口即可。我们定义一个内部类来重载()将这个类作为第三个实例化的模板参数传入红黑树中。我们在对迭代器重命名的时候加上一个typename进行修饰，告诉编译器这是一个类型而不是类中的一个变量。这里map重点实现了这个[ ]重载，这里是调用的insert函数来实现的，这样即可以查找对应的val值，还可以插入新的键值对，同时也可以修改对应的val值，简直是妙不可言。

template<class K>
class Set
{

public:
	struct SetKeyOft
	{
		const K& operator()(const K& key)
		{
			return key;
		}
	};

public:
  typedef typename RBTree<K, K, SetKeyOft>::iterator iterator;
  iterator begin()
  {
	  return _t.begin();
  }

  iterator end()
  {
	  return _t.end();
  }

  pair<iterator, bool> insert(const K& key)
  {
	  return _t.Insert(key);
  }
private:
	RBTree<K, K, SetKeyOft> _t;
};

Set同样也是如此，复用红黑树的接口即可。这里同样实现了一个内部类进行作为红黑树的实例化的第三个参数用于来控制这个比较逻辑。这里map和set和内部类是控制红黑树中节点中谁和谁进行比较，set的话只有key这个肯定是key和key进行比较，但是map是键值对，这里就是用来控制红黑树中的pair节点是通过key来进行比较的。如果我们想要实现比较逻辑的话，我们还可以加上一个模板参数，用来接收比较的仿函数。

2.简单测试

#include<iostream>
#include"Map.h"
#include"Set.h"
using namespace std;
void test_Set1()
{
	int a[] = { 11, 1, 7, 10, 14, 11, 22, 14, 15,89 };
	Set<int> s;
	for (auto e : a)
	{
		s.insert(e);
	}

	Set<int>::iterator it = s.begin();
	while (it != s.end())
	{
		cout << *it << " ";
		++it;
	}
	cout << endl;
	for (auto e : s)
	{
		cout << e << " ";
	}
	cout << endl;
}
void test_Map1()
{
	Map<string, string> dict;
	dict.insert(make_pair("sort", "排序"));
	dict.insert(make_pair("string","字符串"));
	dict.insert(make_pair("count", "计数"));
	dict.insert(make_pair("left", "左边")); 

	Map<string, string>::iterator it = dict.begin();
	while (it != dict.end())
	{
		cout << it->first << ":" << it->second << endl;
		++it;
	}
	
	cout << endl;

	for (auto& kv : dict)
	{
		cout << kv.first << ":" << kv.second << endl;
	}
	cout << endl;
}

void test_Map2()
{
	string arr[] = { "苹果", "苹果", "梨子", "梨子", "香蕉", "香蕉", "香蕉", "哈密瓜", "草莓", "火龙果" };
	Map<string, int> countMap;
	for (auto& e : arr)
	{
		countMap[e]++;
	}

	for (auto& kv : countMap)
	{
		cout << kv.first << ":" << kv.second << endl;
	}
}
int main()
{
	test_Map1();
	test_Map2();
	test_Set1();
}

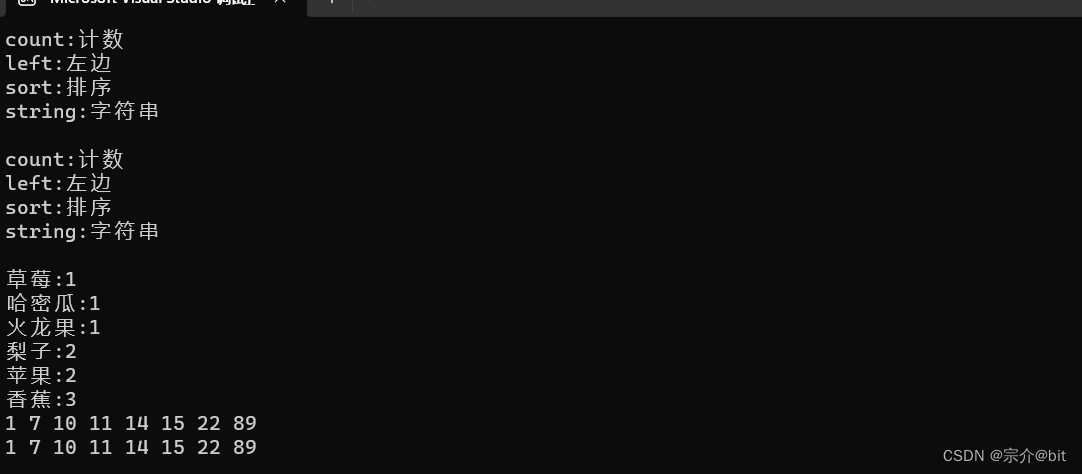
在这里插入图片描述

从打印结果上来看，我们封装的map和set基本实现了插入节点的功能，迭代器也正确实现出来了。以上便是对map和set的简单封装，总的来说就是模板套一层模板的意思。最里面是红黑树的壳子，通过这套壳子来实例化出不同的容器。这里的模板复用技巧非常值得我们学习，比如红黑树模板参数的确定以及相关的意义。为啥要这么设计，都是值得我们细细揣摩的。

以上内容，如有问题，欢迎指正！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/566327.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

FPGA采集CameraLink相机Base模式解码输出，附带工程源码和技术支持

FPGA采集CameraLink相机Base模式解码输出，附带工程源码和技术支持

目录 1、前言2、CameraLink协议基础3、目前我已有的CameraLink收发工程4、设计方案输入CameraLink相机LVDS视频解码视频缓存视频输出软件配置 5、vivado工程详解6、上板调试验证7、福利&#xff1a;工程代码的获取 1、前言 FPGA实现CameraLink视频编解码目前有两种方案&#x…
阅读更多...
华为OD机试真题 Java 实现【分界线】【2023Q1 100分】

华为OD机试真题 Java 实现【分界线】【2023Q1 100分】

一、题目描述 电视剧《分界线》里面有一个片段&#xff0c;男主为了向警察透露案件细节&#xff0c;且不暴露自己&#xff0c;于是将报刊上的字剪切下来&#xff0c;剪拼成匿名信。现在有一名举报人&#xff0c;希望借鉴这种手段&#xff0c;使用英文报刊完成举报操作。 但为…
阅读更多...
day15 - 使用图像金字塔进行图像拼接

day15 - 使用图像金字塔进行图像拼接

在我们之前的学习过程中&#xff0c;使用的都是恒定大小的图像&#xff0c;但是在某些情况下&#xff0c;我们需要使用不同分辨率的&#xff08;相同&#xff09;图像。例如&#xff0c;当在图像中搜索某些东西&#xff08;例如人脸&#xff09;时&#xff0c;我们不确定对象将…
阅读更多...
vim各模式下常见指令集

vim各模式下常见指令集

vim简介 vim其实就是一款写代码的软件或者编辑器。vs2019能够编写编译调试运行代码&#xff0c;它的功能非常的集成&#xff0c;因此它被称为集成开发环境。但是vim只是编辑&#xff0c;他的核心工作就是文本编写&#xff0c;就是单纯写代码&#xff0c;因此它的功能是不集成的…
阅读更多...
chatgpt赋能python：Python概览：了解Python的优势和应用领域

chatgpt赋能python：Python概览：了解Python的优势和应用领域

Python概览&#xff1a;了解Python的优势和应用领域 介绍Python Python是一门高级编程语言&#xff0c;由Guido van Rossum在1989年创建&#xff0c;旨在提高开发人员的开发效率和代码质量。Python有着良好的代码可读性和简洁性&#xff0c;因此它已成为全球最受欢迎的编程语…
阅读更多...
如何在 IDEA 中生成 Maven 依赖关系图？

如何在 IDEA 中生成 Maven 依赖关系图？

文章目录 1、查看依赖关系图2、保存至本地查看3、exclude IDEA提供了查看依赖关系的方式&#xff0c;如下&#xff1a; 1、查看依赖关系图 点击IDEA右侧的maven工具栏&#xff0c;展开maven操作界面。 进入maven操作界面&#xff0c;点击查看maven之间的依赖关系按钮 然后就可…
阅读更多...
代码随想录算法训练营day51 | 309. 最佳买卖股票时机含冷冻期，714.买卖股票的最佳时机含手续费，股票问题总结

代码随想录算法训练营day51 | 309. 最佳买卖股票时机含冷冻期，714.买卖股票的最佳时机含手续费，股票问题总结

代码随想录算法训练营day51 | 309. 最佳买卖股票时机含冷冻期&#xff0c;714.买卖股票的最佳时机含手续费&#xff0c;股票问题总结 309. 最佳买卖股票时机含冷冻期解法一&#xff1a;动态规划 714.买卖股票的最佳时机含手续费解法一&#xff1a;动态规划 股票问题总结 309. 最…
阅读更多...
矿井水除总氮工艺详解

矿井水除总氮工艺详解

一、项目概述 项目背景: 1、水资源浪费长期以来&#xff0c;采煤对地下水造成了严重破坏。绝大部分矿井水&#xff0c;被以直排方式&#xff0c;流入河道、田野&#xff0c;这不仅造成水资源的白白浪费&#xff0c;也污染了环境。社会对此反响强烈的同时&#xff0c;煤矿企业也…
阅读更多...
BT131-ASEMI代理KY原装双向可控硅BT131

BT131-ASEMI代理KY原装双向可控硅BT131

编辑&#xff1a;ll BT131-ASEMI代理KY原装双向可控硅BT131 型号&#xff1a;BT131 品牌&#xff1a;韩景元\KY 封装&#xff1a;TO-92 特性&#xff1a;可控硅 正向电流&#xff1a;1A 反向耐压&#xff1a;600V 触发电压&#xff1a; 0.62&#xff5e;0.8 V 引脚数量…
阅读更多...
ES(Elasticsearch)的docker安装部署教程

ES(Elasticsearch)的docker安装部署教程

0、 服务器版本信息 Red Hat 4.8.5-44 CentOS Linux release 7.9.2009 (Core) 1、ES部署 1.1 拉取docker镜像 docker pull elasticsearch:7.10.1拉取成功的镜像&#xff0c;可以使用如下命令查看&#xff1a; docker images 上图2年之前表示该elasticsearch的7.10.1镜像版…
阅读更多...
从传统 IT 容灾转向“全栈云容灾”｜什么是更适合政企的云

从传统 IT 容灾转向“全栈云容灾”｜什么是更适合政企的云

凌晨 3 点&#xff0c;在某医院的自助缴费机前&#xff0c;一位医患家属正愁眉紧锁&#xff0c;手中的医保卡已经刷了无数遍&#xff0c;可次次都提示缴费失败&#xff0c;至亲的手术已经迫在眉睫… 早上 8 点&#xff0c;是上班族在通勤途中打开新闻 app 刷新闻的高峰&#x…
阅读更多...
vue3+vite 中使用百度地图【两种方式】

vue3+vite 中使用百度地图【两种方式】

vue3vite项目中使用百度地图 方式一&#xff1a;直接使用百度地图的ak方式二&#xff1a;使用vue-baidu-map-3x插件 方式一&#xff1a;直接使用百度地图的ak 提前准备&#xff1a; 创建一个vite项目申请好的百度地图ak值 百度地图使用&#xff1a; 在创建好的vite项目的入…
阅读更多...
python 编译安装与脚本安装

python 编译安装与脚本安装

编译安装的一般步骤&#xff1a; 安装依赖&#xff0c;安装依赖的第三方的工具&#xff0c;yum可以解决 编译安装的包中都有&#xff1a;configure 文件 进行预编译&#xff1a;检查你的环境是否合格 ./configure --prefixxxx 生成编译的文件&#xff1a;MakeFile python安装&…
阅读更多...
Taobao.item_search-淘宝商品列表接口、关键词搜索淘宝商品列表接口

Taobao.item_search-淘宝商品列表接口、关键词搜索淘宝商品列表接口

淘宝商品列表接口是淘宝开放平台提供的一个接口&#xff0c;可以返回符合指定条件的商品列表&#xff0c;开发者可以根据自己的需要在自己的应用中使用。 请求方式 淘宝商品列表接口使用 HTTP GET 请求方式。 请求 URL 请求URL如下&#xff1a;http://o0b.cn/opandy 请求参…
阅读更多...
一文读懂循环队列的实现细节

一文读懂循环队列的实现细节

循环队列最早出现在计算机系统设计中&#xff0c;它的出现主要是为了满足实际需求&#xff1a;在存储机制上&#xff0c;传统的队列存储方式难以满足一些实际应用中需要存储大量数据的场景。在有限的数组空间内&#xff0c;传统的队列存储方式可能会出现存储空间浪费过多、存储…
阅读更多...
使用 StarCoder 创建一个编程助手

使用 StarCoder 创建一个编程助手

如果你是一个软件开发者&#xff0c;你可能已经使用过 ChatGPT 或 GitHub 的 Copilot 去解决一些写代码过程中遇到的问题&#xff0c;比如将代码从一种语言翻译到另一种语言&#xff0c;或者通过自然语言&#xff0c;诸如“写一个计算斐波那契数列第 N 个元素的 Python 程序”&…
阅读更多...
[分享] 冒险岛079私服搭建

[分享] 冒险岛079私服搭建

文章目录 前言目录介绍环境介绍过程第一步启动phpStudy.exe第二步 启动服务端.bat第三步 启动登录器.bat 总结常见问题 前言 好几年前找一个079版本冒险岛私服版本&#xff0c;本地玩了一下&#xff0c;感觉不错还研究了一下自带的GM工具。 现在朋友需要&#xff0c;记录一下踩…
阅读更多...
交直流电流钳的用途和使用

交直流电流钳的用途和使用

电流钳是一种非侵入式检测设备&#xff0c;并不要求把采集端接入电路。一旦接入电路&#xff0c;就后会有阻抗的问题。霍尔线圈能够感应交流电流&#xff0c;但是无法感应直流信号。市售的电流钳&#xff0c;仍然是非接触测量&#xff0c;但交直流电流都能采&#xff0c;并且配…
阅读更多...
Java的URI类

Java的URI类

文章目录 1. 简介2. 构造一个URI3. URI的各个部分4. 解析相对URI5. 相等性和比较6. 字符串表示 1. 简介 URI是对URL的抽象&#xff0c;不仅包含统一资源定位符&#xff0c;还包括统一资源名&#xff08;URN&#xff09;。实际使用的URI大多是URL&#xff0c;但大多数规范和标准…
阅读更多...
spring高频面试题

spring高频面试题

什么是IOC Spring框架提供的一种容器,用于控制对象的创建和对象之间的调用&#xff0c;通过IOC容器把对象的创建和调用过程交给Spring进行管理&#xff0c;省去了使用 new的方式创建对象。 所谓依赖注入(DI)&#xff0c;就是由IOC容器在运行期间&#xff0c;动态地将某种依赖关…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023