文章目录
- 抛出问题:引入位图
- 位图解决
- 位图的概念
- 位图的实现
- 结构
- 构造函数
- 设置位
- 清空位
- 判断这个数是否存在
- 反转位
- size与count
- 打印函数
- 位图的应用
抛出问题:引入位图
问题:给40亿个不重复的无符号整数,没排序,给一个无符号整数,如何快速判断这个数是否在这40亿个数中。
解题思路:
- 遍历,时间复杂度O(N);
- 先排序(O(NlogN)),再利用二分查找(logN)。
- 放到哈希表或者红黑树。
现在我们来分析一下上面的思路是否可行。首先我们要知道40亿个无符号整数占用多少空间:1G=1024MB=1024x2024KB=1024x1024x1024Byte,约等于10亿字节,所以40亿个无符号整数(一个整数需要占用4个字节)需要占用约16G的内存空间。
40亿个无符号整数需要16G的空间,那我们就只能采用归并排序了,但是二分查找算法没办法在文件中完成,所以思路1不适用。
如果放到哈希表或红黑树,我们首先要把文件中的数据加载到内存,可以采用分步加载,然后还要将这些数据插入到哈希表或红黑树中,构建完成后,再find数据。那还不如暴力查找,对吧。
综上,以上几种思路不适用的重要原因是:内存不足。
位图解决
数据是否在给定的整型数据中,结果无非两种,在或不在,那么我们就可以使用一个二进制比特位来代表数据是否存在,如果二进制比特位为1,代表存在,0代表不存在。往往我们可以将整数转换成char去存储,一个char等于1个字节=8个比特位,这样40亿个无符号整型就大概只需要0.5G的内存空间。比如:
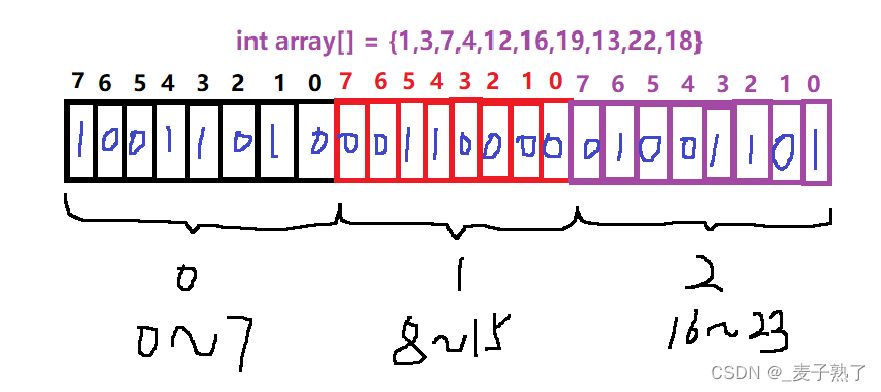
位图的概念
位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的处理,通常是用来判断某个数据是否存在。
位图的实现
结构
- 采用字符数组
- 采用非类型模板参数,N表示要设置的bit位数
namespace zxn
{
//模拟实现位图
template<size_t N>
class bitset
{
public:
//构造函数
bitset();
//设置位
void set(size_t x);
//清空位
void reset(size_t x);
//判断数据是否存在
bool test(size_t x);
//反转位
void flip(size_t pos);
//获取可以容纳的位的个数
size_t size();
//获取被设置位的个数
size_t count();
//打印函数
void Print();
private:
vector<char> _bits; //位图
};
}
构造函数
N是非类型模板参数,表示我们需要设置的bit位数,因为我们采用字符数组,存储的类型是char,char类型占一个字节,所以N/8+1表示我们需要的char类型空间。利用resize函数,开空间的同时将其初始化为0。
//构造函数
bitset()
{
_bits.resize(N / 8 + 1, 0);
}
设置位
如何将数据对应的比特位设置为1(存在)?
这里注意区分左移<<,右移>>,和虚拟内存当中的低地址,高地址。
- 回顾大小端的概念
大端字节序:低位存在高地址
小端字节序:低位存在低地址

注意:读的时候是从低地址到高地址>
- 为什么采用左移位(观察虚拟内存地址)

void set(size_t x)
{
//计算数据x映射的比特位在第i个char数组的位置
size_t i = x / 8;
//计算数据x映射的比特位在这个char的第j个比特位
size_t j = x % 8;
_bits[i] |= (1 << j);
}
清空位
reset函数的功能是将一个数据对应的比特位设置为不存在。
void reset(size_t x)
{
//计算数据x映射的比特位在第i个char数组的位置
size_t i = x / 8;
//计算数据x映射的比特位在这个char的第j个比特位
size_t j = x % 8;
_bits[i] &= ~(1 << j);
}
判断这个数是否存在
test函数的功能是判断这个无符号正常是否在这40亿个不重复的数据中。如果这个数据对应的比特位状态为1,就说明这个数据存在,返回true。
bool test(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
return _bits[i] & (1 << j);
//或return (_bits[i]<<j)&1;
}
反转位
- 计算出数据对应的比特位位置。
- 将1左移j位与char中的第i个比特位进行异或运算。(相异为1,相同为0)
//反转位
void flip(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
_bits[i] ^= (1 << j);//异或:相异为1,相同为0
}
size与count
//获取可以容纳的比特位个数
size_t size()
{
return N;
}
获取位图中1的个数方法:
- 将原树n与n-1进行&与运算得到新的n;
- 判断n是否为0,若n不为0则循环进行第一步。
- 如此循环进行下去,直到n最终为0,该代码被执行了几次就代表二进制位中有多少个1。
原理:n&(n-1)该操作每进行一次就会消去二进制最右边的1。

//获取比特位为1的个数
size_t count()
{
size_t count = 0;
for (auto e : _bits)
{
//e是char类型的
while (e)
{
e = e & (e - 1);
count++;
}
}
return count;//被设置位的个数,即位图中1的个数
}
打印函数
打印函数的功能是:遍历位图,打印每个比特位,在打印的过程中也可以统计位的个数。
void Print()
{
int count = 0;
size_t n = _bits.size();//便于获取数组的最后一个字符
//先打印前n-1个char
for (size_t i = 0; i < n - 1; i++)
{
for (size_t j = 0; j < 8; j++)
{
if (_bits[i] & (1 << j))
{
cout << "1";
}
else
{
cout << "0";
}
count++;
}
}
//在打印最后一个字符的前N%8位
for (size_t j = 0; j < N % 8; j++)
{
if (_bits[n - 1] & (1 << j))
{
cout << "1";
}
else
{
cout << "0";
}
count++;
}
cout << " " << count << endl;
}
位图的应用
- 快速查找某个数据是否在一个集合中;
- 排序+去重;
- 求两个集合的交集,并集;
- 操作系统中磁盘块标记。
位图的优缺点:
- 优点:速度快,节省空间。
- 缺点:只能映射整型,其它类型,如浮点数,string等等不能存储映射。
问题一:给定100亿个整数,设计算法找到只出现一次的整数。
一个位图中的一个比特位只能表示两种状态,因此我们可以开辟两个位图,这两个位图的对应位置分别表示映射到该位置的整数的第一个位和第一个位。
可以用如下方式标记:
- 00表示不存在,没有出现过
- 01表示出现一次
- 10表示出现过一次以上

代码实现:复用bitset
template<size_t N>
class twobitset
{
public:
//设置位:00 表示出现0次,01表示只出现一次,10表示出现过一次以上
void set(size_t x)
{
//00 -> 01
if (_bs1.test(x) == false && _bs2.test(x) == false)
{
_bs2.set(x);
}
else if (_bs1.test(x) == false && _bs2.test(x) == true)
{
//01 -> 10
_bs1.set(x);
_bs2.reset(x);
}
}
void Print()
{
//遍历整个位图
for (size_t i = 0; i < N; i++)
{
//打印出只出现一次的整数,即第一位为0,第二位为1,01
if (_bs2.test(i))
{
cout << i << endl;
}
}
}
private:
bitset<N> _bs1;
bitset<N> _bs2;
};
void test_twobitset()
{
int a[] = { 3, 45, 53, 32, 32, 43, 3, 2, 5, 2, 32, 55, 5, 53,43,9,8,7,8};
twobitset<100> bs;
//将数组a中的数据映射到位图中
for (auto e : a)
{
bs.set(e);
}
//打印出只出现一次的数据
bs.Print();
}
注意:存储100亿个整数大概需要40G的内存空间,因此数据肯定是存储在文件中的;为了能映射所有整数,位图的大小必须开辟2^32位,即4294967295,因此开辟一个位图大概需要0.5G的内存空间,两个位图就要1G的内存空间,所以代码选择在堆区开辟空间,若是在栈区开辟会导致栈溢出问题。
问题二:给两个文件,分别有100亿个整数,我们只要1G内存,如何找到两个文件的交集。
思路一:
1.依次读取第一个文件的值,读到内存的一个位图中,再读取看一个文件,判断在不在第一个位图中,在就是交集,这个方法大约需要0.5G的内存,但是存在一个问题,就是找出的交集存在重复的值,我们还需要对其进行去重才可以。
2.改进方法:每次找到交集的值,都将第一个位图对应的值设置为0,这样就可以解决找到的交集有重复值的问题。
思路二:
1.依次读取文件1的数据映射到位图1;
2.依次读取文件2的数据映射到位图2;
3.将位图1和位图2的数据进行与&&操作,结果为1的就是交集。
问题三:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数。
这道题目的思路和题目1是一样的,我们可以用以下四种二进制表示四种状态:
- 00 出现0次
- 01 出现1次
- 10 出现2次
- 11 出现2次以上
#include <iostream>
#include <vector>
#include <bitset>
using namespace std;
int main()
{
int a[] = { 3, 45, 53, 32, 32, 43, 3, 2, 5, 2, 32, 55, 5, 53,43,9,8,7,8,55};
//在堆上申请空间
bitset<4294967295>* bs1 = new bitset<4294967295>;
bitset<4294967295>* bs2 = new bitset<4294967295>;
for (auto e : a)
{
if (!bs1->test(e) && !bs2->test(e)) //00->01
{
bs2->set(e);
}
else if (!bs1->test(e) && bs2->test(e)) //01->10
{
bs1->set(e);
bs2->reset(e);
}
else if (bs1->test(e) && !bs2->test(e)) //10->11
{
bs2->set(e);
}
}
for (size_t i = 0; i < 4294967295; i++)
{
if ((!bs1->test(i) && bs2->test(i)) || (bs1->test(i) && !bs2->test(i))) //01或10
cout << i << endl;
}
return 0;
}