一,有向无环图DAG描述表达式
1.DAG
若一个有向图中不存在环,则称为有向无环图,记为DAG。
2.用二叉树描述表达式
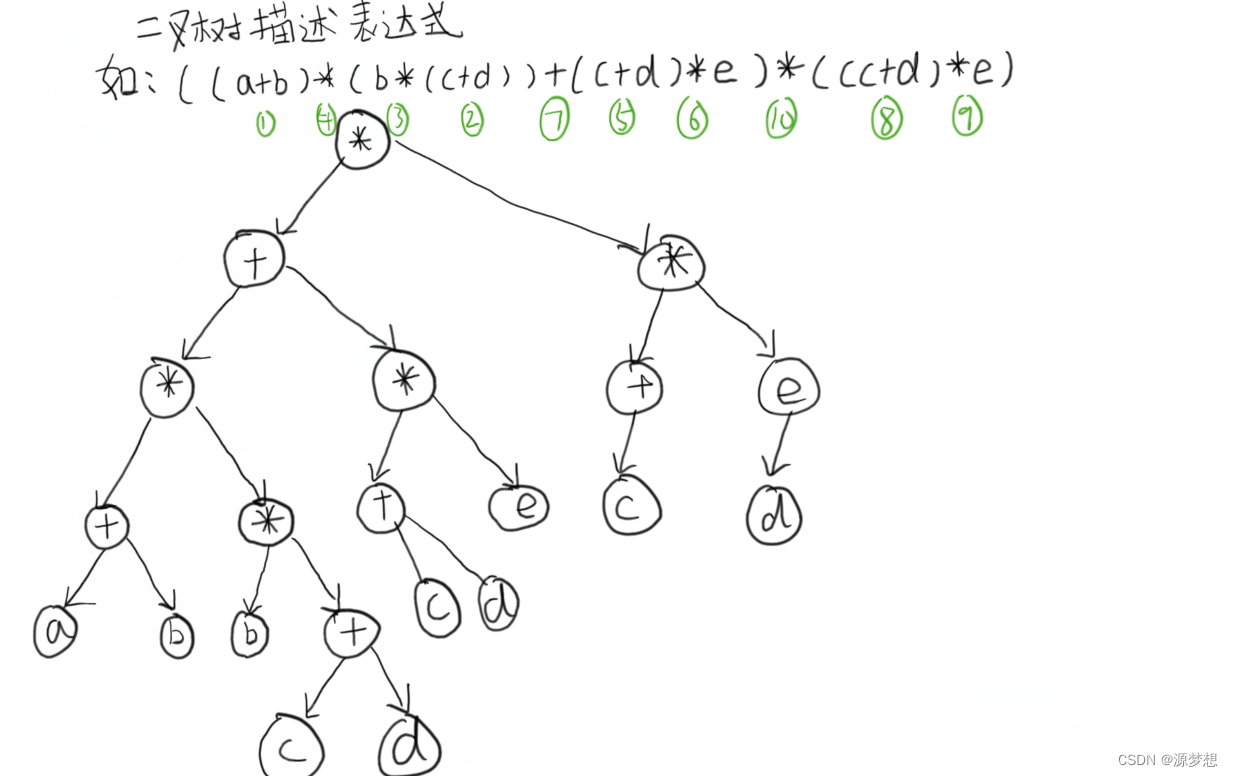
3.用DAG描述表达式
用二叉树描述表达式有缺点,有些结点大可不必存储,可以共用。
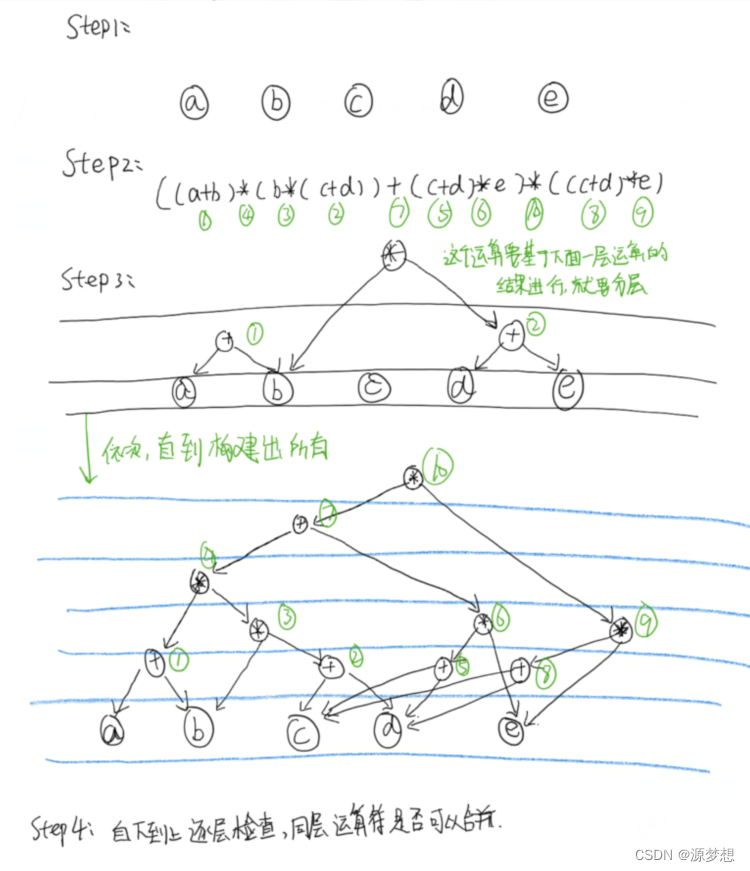
step1:把各个操作数不重复的排成一排。
step2:标出各运算符生效顺序。
step3:按顺序加入运算符注意分层。
step4:从底层上逐层检查同层的运算符是否可以合并。
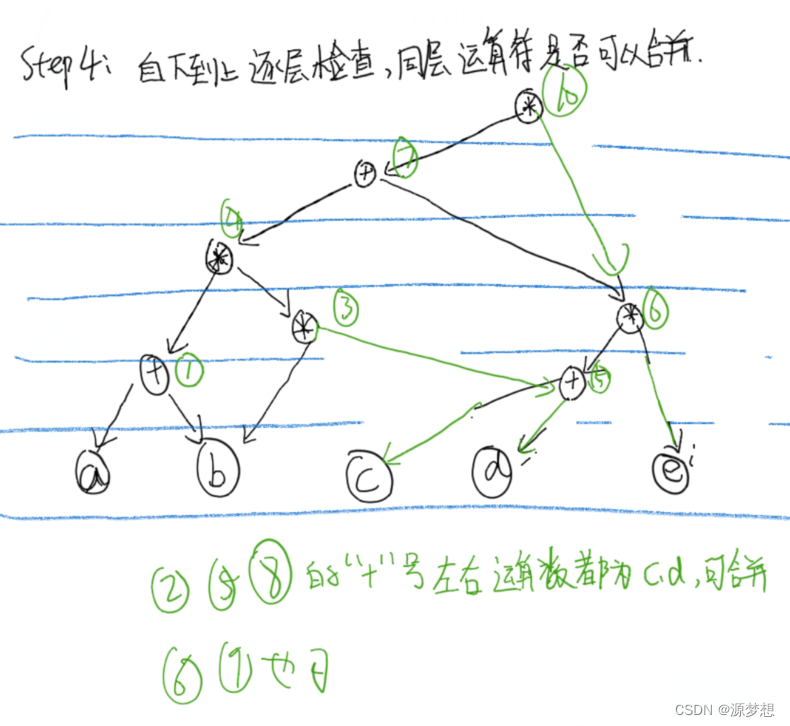
二,拓扑排序AOV网
1.AOV网
用DAG表示一个工程,顶点表示活动,边<Vi,Vj>表示 活动Vi 必须先于 活动Vj 进行的这样一种关系,则将这种有向图称为 顶带你表示活动的网络,记为AOV网。
2.拓扑排序
有一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序:
①每个顶顶只出现一次
②若顶点A在序列中排在顶点B的前面,则在图中不存在从顶点B到顶点A的路径。即,无环
3.拓扑排序步骤
拓扑排序的算法有很多,下面是常见的:
①从AOV网中选择一个没有前驱的顶点并输出。
②从网中删除该顶点和所有以它为起点的有向边
③重复上述过程,直至AOV为空,或者当前网中不存在无前驱的顶点为止。
4.逆拓扑排序
删除出度为0的顶点。
5.代码实现
1.常规实现
2.用BFS实现
三,关键路径AOE网
1.AOE网
再带权有向图中,以顶点表示事件,以有向边表示活动,以边上权值表示完成该活动的开销(如:完成该活动时间),称之为用边表示活动的网络,简称AOE网。
注1:AOE与AOV都是有向无环图DAG。
注2:AOE与AOV区别在于他们顶点和边的意义不同。
注3:AOE与AOV区别在于,AOE网中边有权值,AOV中仅代表前后关系。
2.几个参量的定义
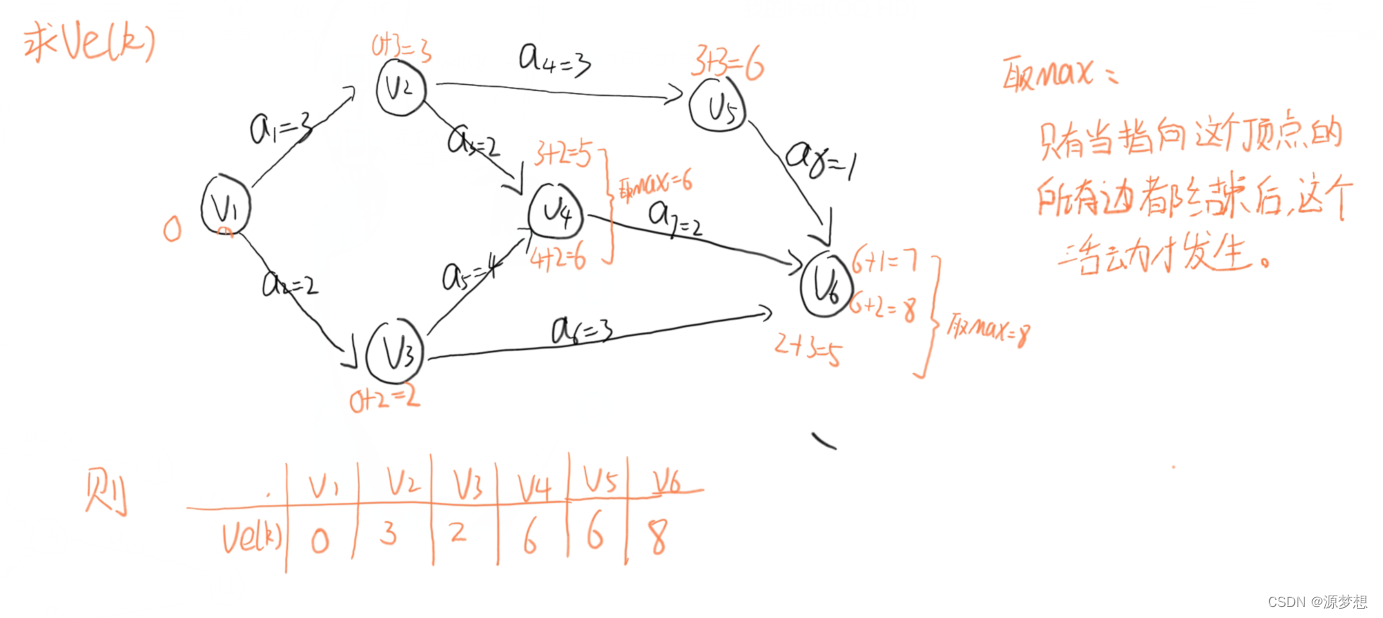
①Ve(k) : 事件Vk的最早发生时间。
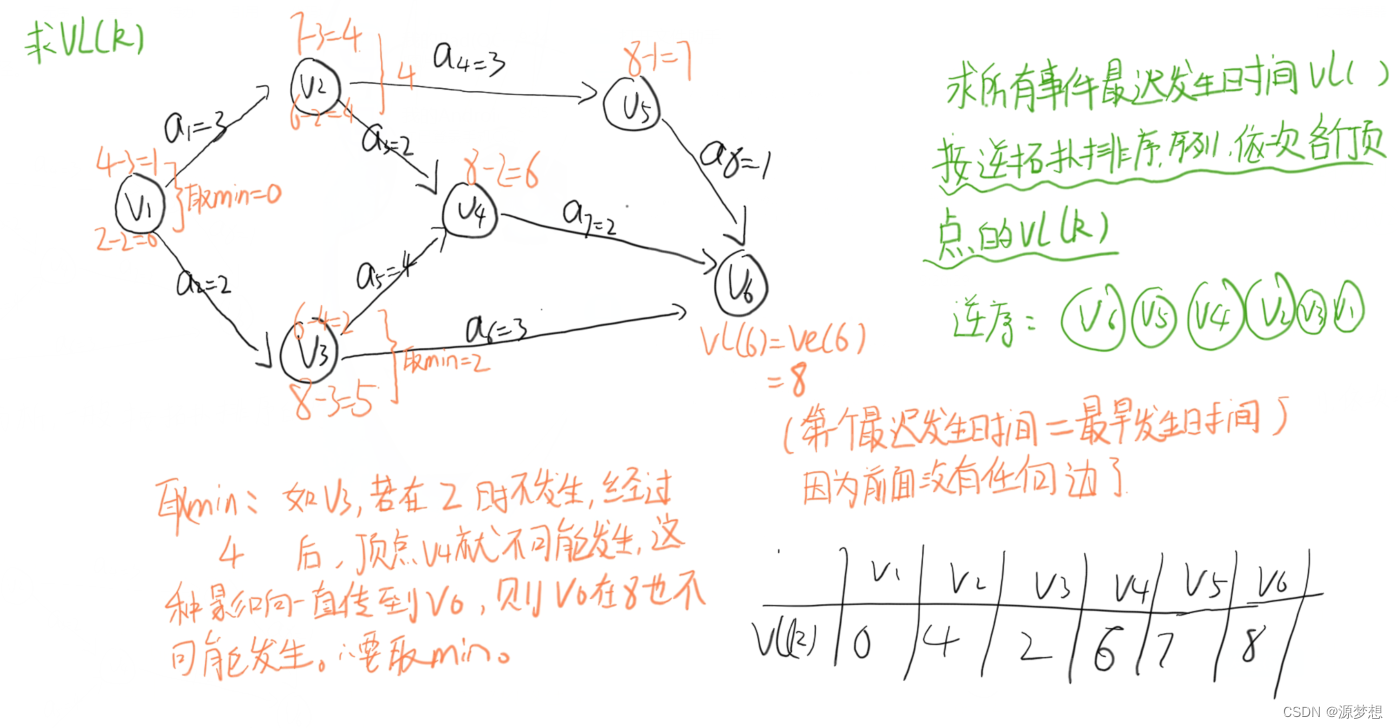
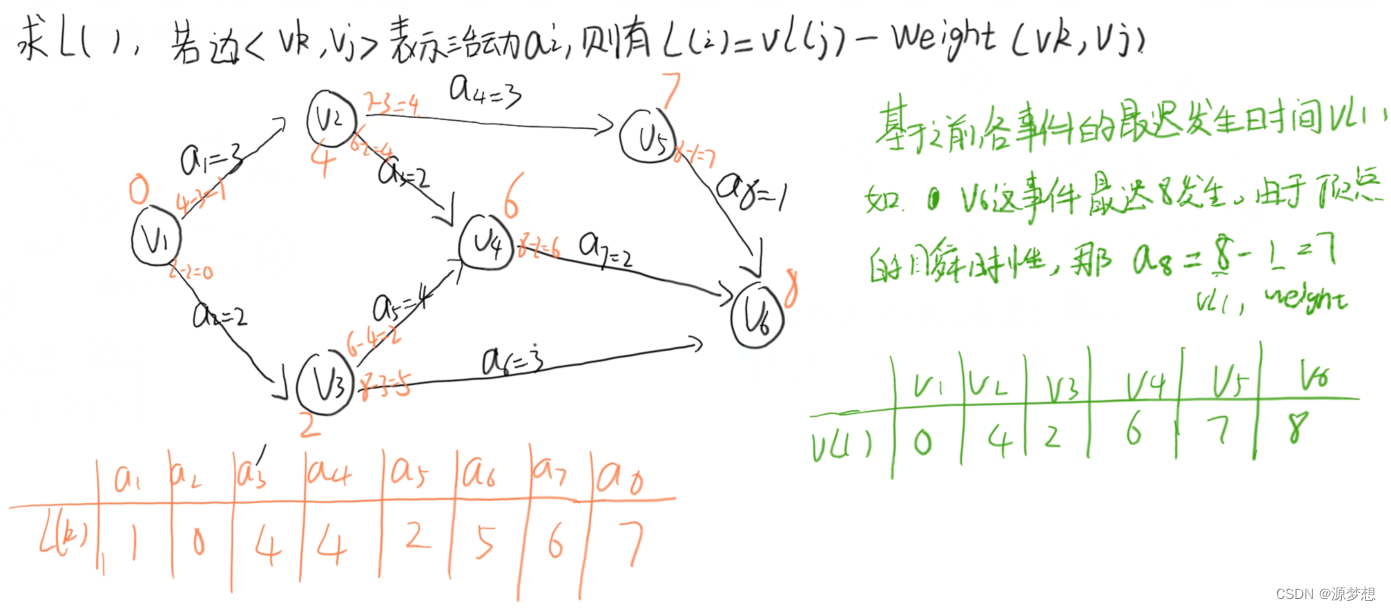
②Vl(k) : 事件Vk的最迟发生时间。
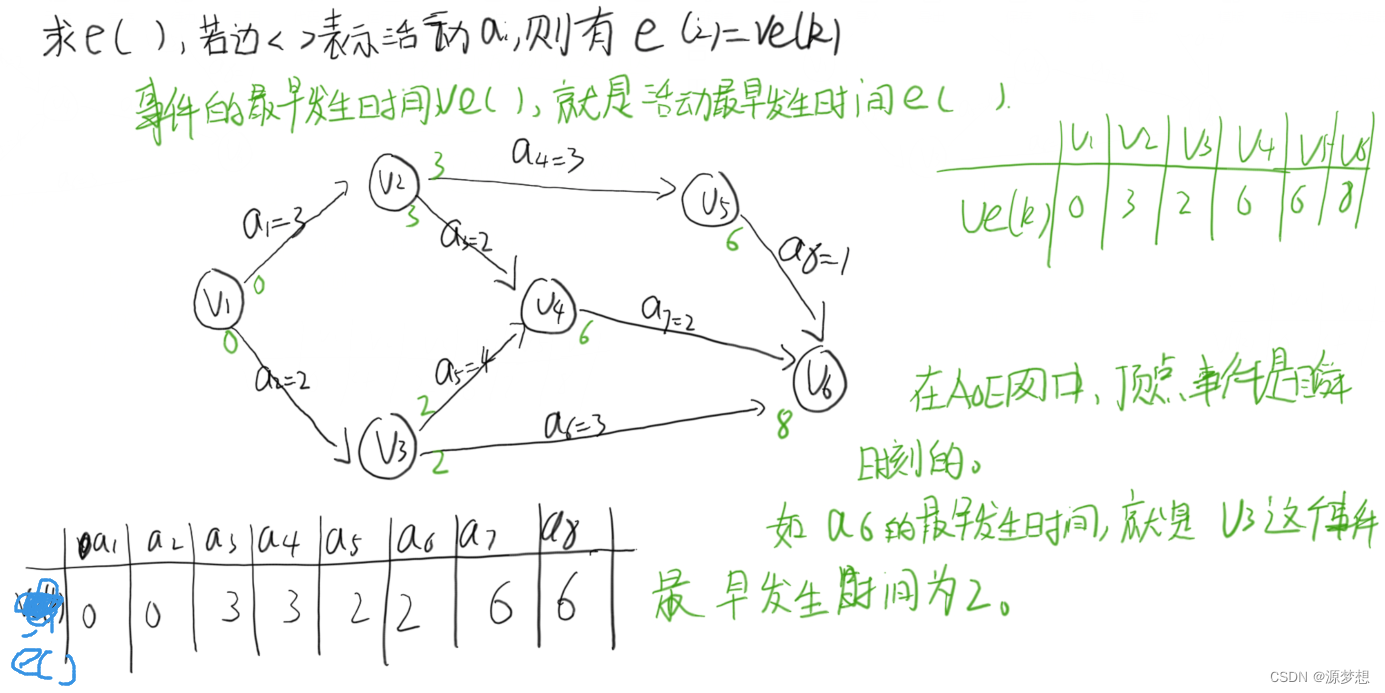
③e(i) : 活动ai的最早开始时间。
④l(i) : 活动ai的最迟开始时间。
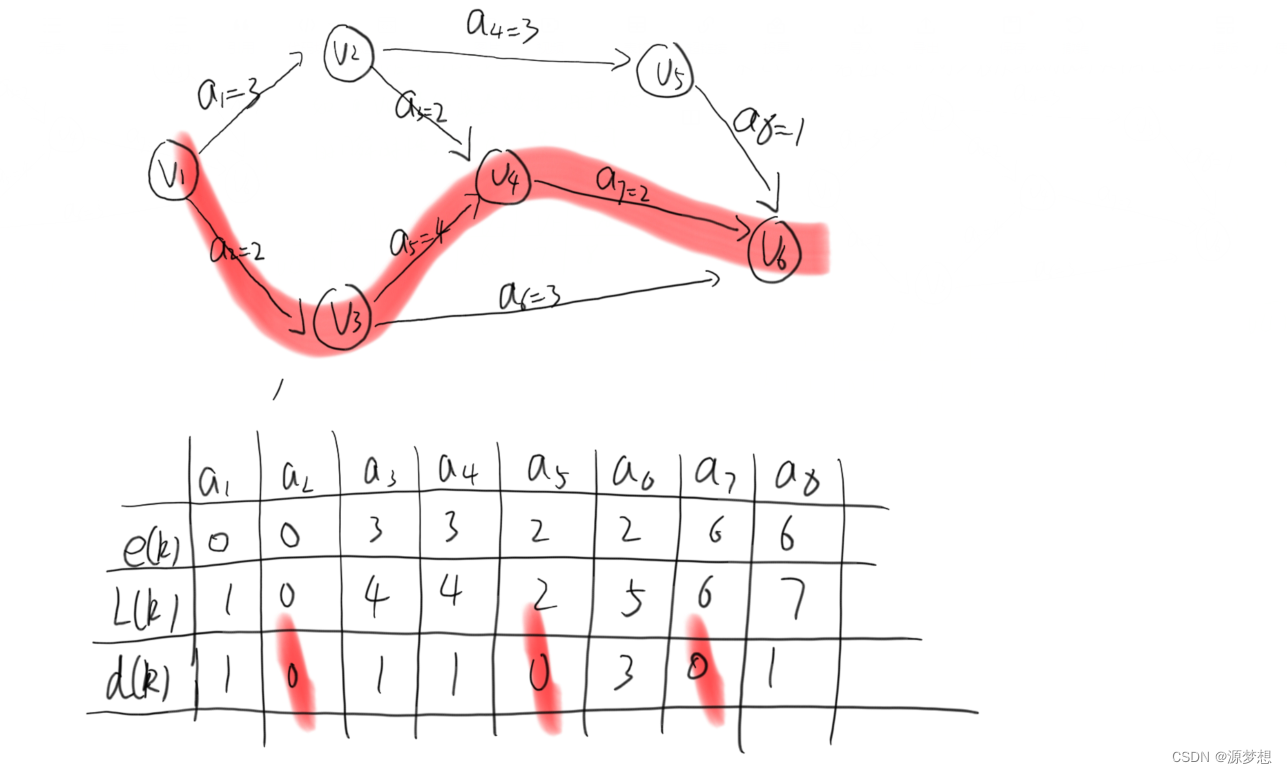
⑤d(i):余量 d(i) = l(i) - e(i)。
注:d(i) = 0的路径,即为关键路径。
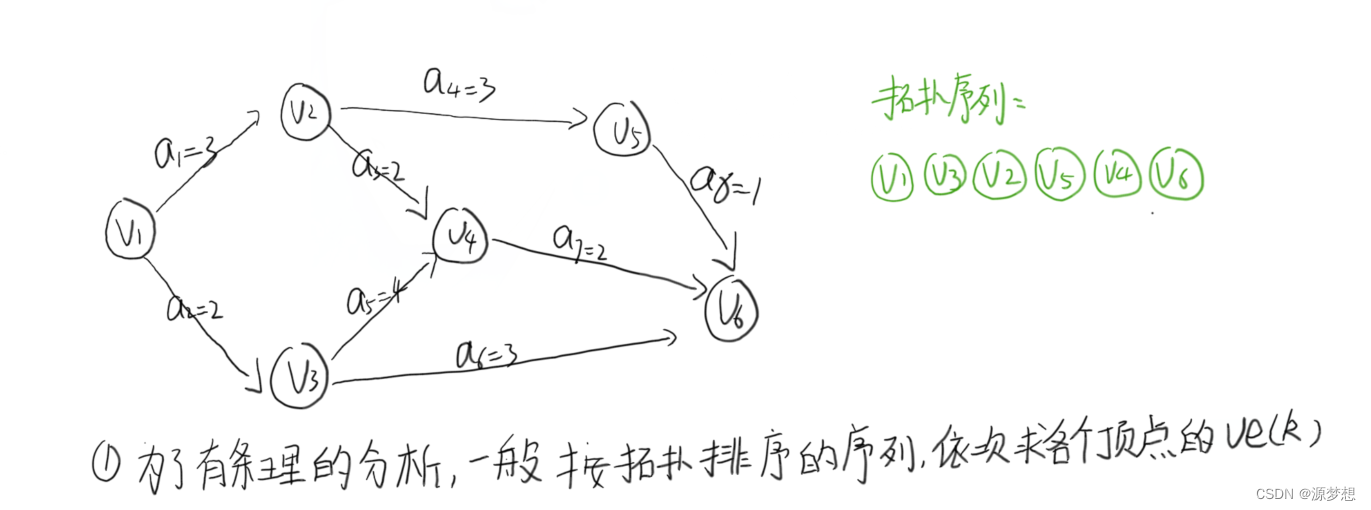
3.关键路径步骤
①求出所有事件最早发生时间Ve()
①求出所有事件最迟发生时间Vl()
①求出所有活动最早开始时间e()
①求出所有活动最迟开始时间l()
①求出所有活动的余量d()
注1:由Ve() 可知 e()。
注2:由Vl() 可知 l()。
注3:由e() 和 l() 可知 d()。
注4:由d() = 0,可找到关键路径。