回溯算法的本质
是穷举,穷举所有可能,然后选出合适的答案,一般用于解决以下类型的问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
回溯算法模板:
返回值一般为void
void backtravel(参数)
终止条件
if (终止条件)
{
存放结果
return;
}
回溯搜索过程
for(循环条件)//实现横向遍历
{
处理节点;
backtravel();//自己调用自己,进行递归,实现纵向遍历
回溯,撤销处理结果
}
//本质上实现了穷举
第77题 组合


解题思路:
class Solution {
public:
vector<vector<int>> result;//存放符合条件结果的集合(大集合)
vector<int> res;//存放符合条件的结果集合(小集合)
void backtravel(int n,int k,int start)
{
if(res.size() == k)//终止条件,当存放结果满足条件,放入大集合
{
result.push_back(res);
return;
}
for(int i = start;i <= n;i++)
{
res.push_back(i);//把挑选的第一个数放入res中
//开始挑选第二个数
backtravel(n,k,i+1);
//找到满足的结果之后,再找下一个满足条件的组合,需要把刚刚的数剔除
res.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
//直接用for循环暴力求解会有一个问题,即k为多少就需要多少层for循环,
//当k特别大的时候,本身代码实现就是不可能的,
//因此采用回溯,精简代码量,但本质上还是穷举,时间复杂度上没有多少精简
//回溯三部曲
//定义回溯函数
backtravel(n,k,1);//第三个参数表示开始挑选元素的位置
return result;
}
};
第216题 组合总和Ⅲ


解题思路:与上一题类似,同样是使用回溯,这里面加了一个剪枝操作,即当剩余待选数字已经凑不够k个数,就没有必要再选了。
class Solution {
public:
vector<vector<int>> result;//存放大结果
vector<int> res;//存放小结果
void backTravel(int start, int k, int n,int sum)
{
//若当前求和已经大于n了,直接结束本次递归
if (sum > n)
return;
//当组合大小满足条件时,判断求和是否满足
if (res.size() == k)
{
if (sum == n)
result.push_back(res);//若满足,直接存下当前组合
return;
}
for (int i = start; i <= 9 - (k - res.size()) + 1; i++)//剪枝操作
{
res.push_back(i);
sum = sum + i;
backTravel(i + 1, k, n,sum);
//开始回溯
res.pop_back();
sum = sum - i;
}
}
vector<vector<int>> combinationSum3(int k, int n) {
//从1开始递归选择,sum初值为0
backTravel(1, k, n, 0);
return result;
}
};
第17题 电话号码的字母组合


**解题思路:**根源上还是组合问题,主要是将每个按键对应的字母实现列出来,然后递归组合就行,注意细节问题,刚开始输入的是字符串,要将字符转换成整型变量。
class Solution {
public:
vector<string> result;
string res;
const string letterMap[10] = {
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz", // 9
};
void backTravel(string digits, int len, int start)
{
if (res.size() == len)//当组合长度满足len,存入结果集
{
result.push_back(res);
return;
}
//计算当前按的数字
int num = digits[start] - '0';
//找这个数字对应的所有字母
string str = letterMap[num];
for (int i = 0; i < str.size(); i++)
{
//开始递归加回溯
res.push_back(str[i]);
backTravel(digits, len, start + 1);
res.pop_back();
}
}
vector<string> letterCombinations(string digits) {
if (digits.size() == 0)
return result;
int len = digits.size();
//从digits的第0位开始组合
backTravel(digits, len, 0);
return result;
}
};
第39题 组合总和


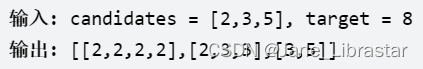
**解题思路:**整体思路不变,注意可以重复选值,所以进入递归的时候不用进行i+1操作。由于是求和操作,累加结果会越来越大,为了降低时间复杂度,我们可以事先将数组按照升序排序,这样当累加值大于target是,就可以不用继续往下递归了。
class Solution {
public:
vector<vector<int>> result;
vector<int> res;
void backTravel(vector<int> candidates,int target,int start,int sum)
{
if(sum > target)
return;
else if(sum == target)
result.push_back(res);
else
{
for (int i = start; i < candidates.size() && sum + candidates[i] <= target; i++)//”剪枝操作“
{
res.push_back(candidates[i]);
//因为可以重复选,所以每次递归都可以从当前位置开始挑选
sum += candidates[i];
backTravel(candidates,target,i,sum);
sum -= candidates[i];
res.pop_back();
}
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());//对数组排个序
backTravel(candidates,target,0,0);
return result;
}
};
第40题 组合总和Ⅱ

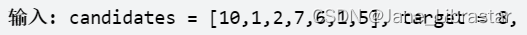

**解题思路:**这个题难点在于有重复数据,但是不能有重复组合,即【1,2,5】不能出现两次,因此,在上一题的基础上,我们要加一个控制条件,即在数组整体排好序的情况下,在for循环(横向选数)中,若当前数据与前一次循环的数据一样是,就代表这个数已经做过组合选择了,就不需要再对他进行选择,直接跳过本次循环。例如上述数组排好序为【1 1 2 5 6 7 10】,当我们对第一个1递归选择组合结束之后,来到第二个1,这时候发现跟前面的数一样,那就不需要对它递归进行二次组合了,这样就实现了去重。(注意,再回溯算法中,for循环控制的是横向选择,递归控制的是纵向选择,对横向选择进行控制不会影响纵向的选择,因此 【1 1 6】这个组合不会被筛掉,因为这里面的1 1是通过递归选择的,而 【1 2 5】 【1 2 5】这里面的两个1是在for循环中,1被挑选了两次,这是不可以的,所以要加以控制)。
class Solution {
public:
vector<vector<int>> result;
vector<int> res;
void backTravel(vector<int> candidates,int target,int start,int sum)
{
if(sum > target)
return;
else if(sum == target)
result.push_back(res);
else
{
for (int i = start; i < candidates.size() && sum + candidates[i] <= target; i++)
{
//去重操作
if(i>start && candidates[i] == candidates[i-1])
continue;
res.push_back(candidates[i]);
//hmap[candidates[i]] -= 1;
//因为不可以重复选,所以每次递归都不能从当前位置开始挑选
sum += candidates[i];
backTravel(candidates,target,i+1,sum);
sum -= candidates[i];
//hmap[candidates[i]] += 1;
res.pop_back();
}
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());
map<int, int> hmap;
backTravel(candidates,target,0,0);
return result;
}
};
第131题 分割回文串

解题思路: 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中再切割第三段…对于字符串“aab”,事先切割出来“a”,“a”是回文串,从下一个位置开始切割“a”,同样,又是一个回文串,再继续切割,“b”是回文串,此时,整个字符串遍历完毕,回溯;从第二个a开始,“ab”不是回文,此次递归结束,回溯;回到第一个a,本次切割就是“aa”了,“aa”是回文,再切,只剩“b”了,还是回文,此次切割结束,回溯;最后一次切割就是“aab”了,不是回文,全部切割结束。
class Solution {
public:
vector<vector<string>> result;
vector<string> res;//存放小结果
void backTravel(const string& s,int start)
{
if(start >= s.size())//当起始位置超过字符串长度
{
result.push_back(res);//把当前的切割结果放入result
return;
}
for(int i = start;i<s.size();i++)
{
//获取[start,i]之间的字符串是否是回文串
if(isPalindrome(s,start,i))//若当前切割的字串是回文串
{
string str = s.substr(start,i-start+1);
res.push_back(str);
}
else //若不是回文串,跳过当前切割
continue;
backTravel(s,i+1);//寻找i+1起始位置的字串
res.pop_back();
}
}
bool isPalindrome(const string& s,int start,int end)
{
for(int i = start,j = end;i<j;i++,j--)
{
if(s[i] != s[j])
return false;
}
return true;
}
vector<vector<string>> partition(string s) {
backTravel(s,0);
return result;
}
};
第93题 复原IP地址




解题思路: 整体思路跟上一题差不多,都是切割,这里要注意的是在切割的过程中要加分隔符 “.”,所以采用了insert函数追加字符和erase函数删除字符。此外,每次切割都要判断当前子串是否符合要求,具体代码细节在下文都做了注释。
class Solution {
public:
vector<string> result;//记录结果
//判断字符串s的子串【start,end】是否合法
bool isValid(const string& s,int start,int end)
{
if(start > end)
return false;
if(s[start] == '0' && start != end)
return false;//以0开头的数字是不合法的
int num = 0;
for(int i = start;i<=end;i++)
{
num = num * 10 + (s[i] - '0');
if(num > 255)
return false;
}
return true;
}
void backTravel(string& s,int start,int pointNum)
{
if(pointNum == 3)//当字符串中有3个逗点时,代表已经被切割成4段,直接判断第四段是否合法,合法的话,直接放入result
{
if(isValid(s,start,s.size()-1))
result.push_back(s);
return;
}
for(int i = start;i<s.size();i++)
{
if(isValid(s,start,i))//判断【start,i】这段是否符合要求
{
s.insert(s.begin()+i+1,'.');//记得要加分隔符
pointNum++;
backTravel(s,i+2,pointNum);
pointNum--;
s.erase(s.begin()+i+1);
}
else
break;
}
}
vector<string> restoreIpAddresses(string s) {
if (s.size() < 4 || s.size() > 12) return result; // 算是剪枝了
backTravel(s, 0, 0);
return result;
}
};
第78题 子集



**解题思路:**其实就是很简单的组合问题,递归结束条件是子集个数达到要求就停止。
class Solution {
public:
vector<vector<int>> result;
vector<int> res;
void backTravel(vector<int>& nums,int start,int Num)
{
if(result.size()<=Num)
result.push_back(res);
for(int i = start;i<nums.size();i++)
{
res.push_back(nums[i]);
backTravel(nums,i+1,Num);
res.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
int len = nums.size();
int Num = pow(2,len);
backTravel(nums,0,Num);
return result;
}
};
第90题 子集Ⅱ



**解题思路:**跟第40题一样,需要去去重,去重之前需要先对原数组排序,由于有重复数据,所以子集的个数就不是2^len个,直接通过for循环默认结束递归(因为也是全部遍历,for循环结束,整个递归就应该结束了)。
class Solution {
public:
vector<vector<int>> result;
vector<int> res;
void backTravel(vector<int>& nums,int start)
{
result.push_back(res);
for(int i = start;i<nums.size();i++)
{
if(i>start && nums[i] == nums[i-1])
continue;
res.push_back(nums[i]);
backTravel(nums,i+1);
res.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
int len = nums.size();
sort(nums.begin(),nums.end());
backTravel(nums,0);
return result;
}
};
第491题 递增子序列



**解题思路:**这道题麻烦在于既要去重,还不能对原来数组进行排序,若一排序,整个结果就变了。对于最复杂的例子【1,2,3,1,1,1,1】直接用原来的去重方法“i>start && nums[i] == nums[i-1]”就不好用了,因为数组没有排序,最前面的1会和后面的1进行组合,等遍历到后面的第一个1的时候,他们又会组合,这样就会有重复项。为了去重,引入set,记录横向遍历使用过的数字,当这个数字再次出现的时候,就不能用它了,注意是横向遍历的时候判断,不会影响纵向组合!!!
class Solution {
public:
vector<vector<int>> result;
vector<int> res;
void backTravel(vector<int> nums,int start)
{
if(res.size()>1)
result.push_back(res);
unordered_set<int> st;//引入set集合
for(int i = start;i<nums.size();i++)
{
if((!res.empty() && nums[i] < res.back()) || st.find(nums[i]) != st.end())//因为要求递增序列,所以当前数字必须大于等于原子序列的最后一个数字
continue;
st.insert(nums[i]);
res.push_back(nums[i]);
backTravel(nums,i+1);
res.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
backTravel(nums,0);
return result;
}
};
第46题 全排列



**解题思路:**这是个排列问题,和组合的区别是,在组合中【1,2】和【2,1】是一个组合,但是在排列中就是两种排列了。所以我们每次挑选数据的时候,就要从头开始,找那些没有被选过的数据。因此需要借助一个used数组,来判断那些数被用了,哪些没有被用。
class Solution {
public:
vector<vector<int>> result;
vector<int> res;
void backTravel(vector<int>& nums,vector<bool>& used)
{
//当收集元素的个数等于nums数组长度,这一组结束
if(res.size() == nums.size())
{
result.push_back(res);
return;
}
for(int i = 0;i<nums.size();i++)
{
if(used[i] == true)
continue;
used[i] = true;
res.push_back(nums[i]);
backTravel(nums,used);
res.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<bool> used(nums.size(),false);
backTravel(nums,used);
return result;
}
};
第47题 全排列Ⅲ


**解题思路:**这里既要去重,又要排列组合。涉及到去重,就需要对原数组进行排序,因为在排列中,每次都是从头挑选,所以去重的时候要注意,当前这个数和前一个数一样,并且used[i-1] == false才表示真正的去重,因为进入到当前这个数字的时候,之前的数字使用情况都被置false了,所以表示的意思是跟他相同数字已经在前边使用过了,本次循环直接跳过就行。
class Solution {
public:
vector<vector<int>> result;
vector<int> res;
void backTravel(vector<int>& nums,vector<bool>& used)
{
//当收集元素的个数等于nums数组长度,这一组结束
if(res.size() == nums.size())
{
result.push_back(res);
return;
}
for(int i = 0;i<nums.size();i++)
{
// 如果同一树层nums[i - 1]使用过则直接跳过
if((i>0 && nums[i] == nums[i-1]) && (used[i-1] == false))
continue;
if(used[i] == false)
{
used[i] = true;
res.push_back(nums[i]);
backTravel(nums,used);
res.pop_back();
used[i] = false;
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<bool> used(nums.size(),false);
sort(nums.begin(),nums.end());
backTravel(nums,used);
return result;
}
};