在描述多维数据的维度关系时，线性模型无疑应用最多。然而某些情况下，我们关心随着时间变化或随着样本分组，线性关系的具体参数是否发生了变化，即是否发生结构变化Structural break。邹检验Chow test提供了最基本的一种结构变化显著性的检验方法，后续统计学者提供了复杂结构变化的识别和判定方法。

邹检验

邹检验适用于如下情形：

情形1：存在数量已知，位置已知的潜在结构断点。

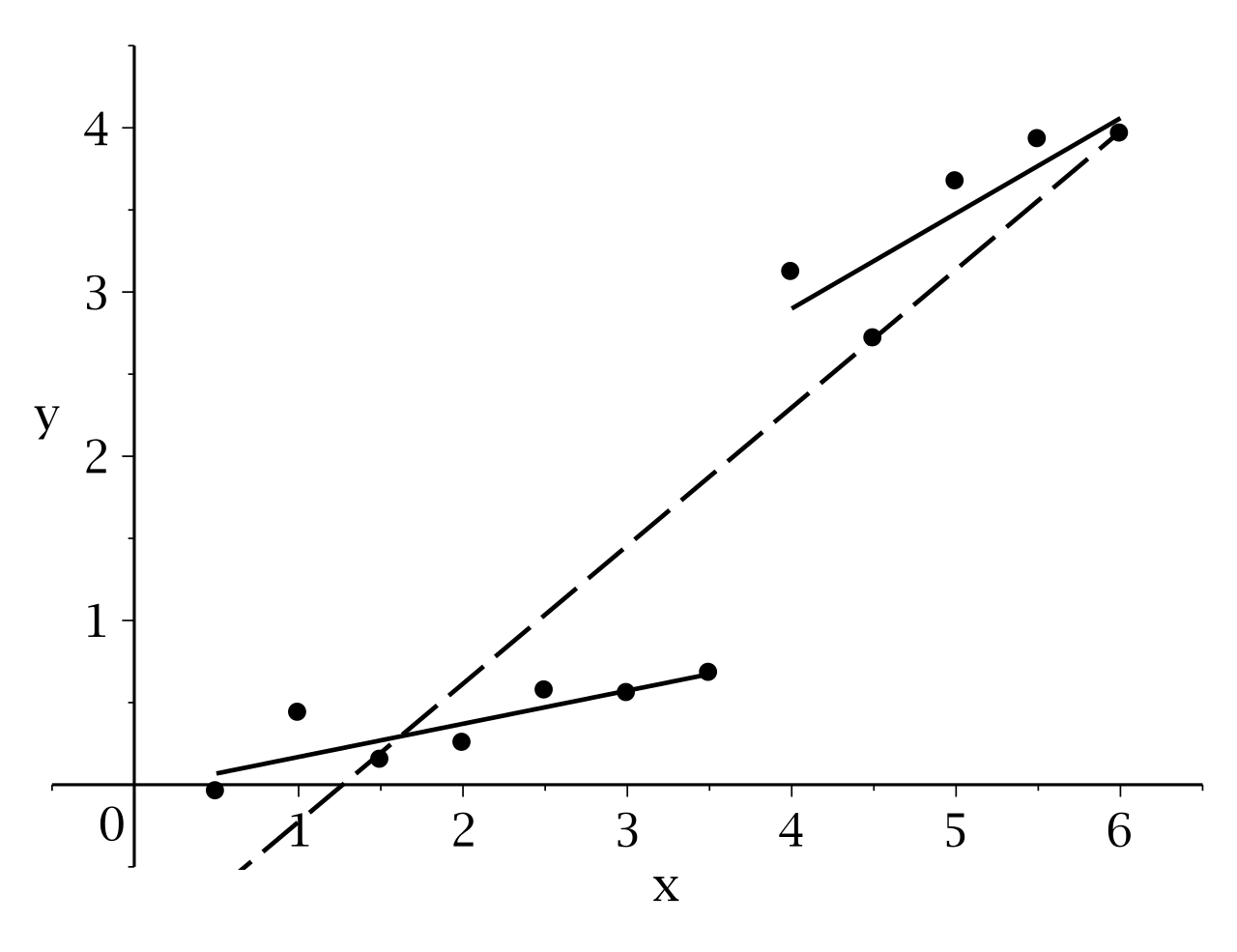
邹检验通过比较总样本回归的残差平方和与分组样本回归残差平方和之间的差值，构造了一个统计变量，该变量符合F分布，可以作为显著性的判断依据。

https://en.wikipedia.org/wiki/Chow_test

一般情形下的结构变化识别

对于更复杂情形下的结构变化：

情形2：存在数量已知，位置未知的潜在结构断点。 情形3：存在数量未知，位置未知的潜在结构断点。 情形4：存在方差的结构断点。

显然邹检验不适用于这些情形。不过如果遍历样本集合应用邹检验，且结果表明所有点均不为断点，则说明情形2和3中，整个区间不存在结构断点。这种检验思路构成sup-F检验，即一系列F检验的上确界均不能拒绝原假设。

针对情形2和3，Andrews(1993,2003)开发了sup-Wald（即一系列Wald检验的上确界）方法，sup-LM（即一系列拉格朗日乘数统计量的上确界）方法和sup-LR（即一系列极大似然比的上确界）方法用以检验结构变化。

针对情形4，Zaman等人(2010,2017)开发了MZ test和sup-MZ test用以检验数据方差是否存在位置已知或位置未知的结构断点。

https://en.wikipedia.org/wiki/Structural_break

结构变化检验的R语言实现

R语言中有strucchange和memochange两个包专门设计用于检验结构变化。其中strucchange已满足基本功能要求。

https://cran.r-project.org/web/packages/strucchange/index.html

strucchange中sctest.formula用于检验线性回归模型中的结构断点，在函数中设定type='Chow'即可实现邹检验。以文档中的例子来做展示：

library(strucchange)

## Example 7.4 from Greene (1993), "Econometric Analysis"
## Chow test on Longley data
data("longley")
sctest(Employed ~ Year + GNP.deflator + GNP + Armed.Forces, data = longley,
       type = "Chow", point = 7)

结果显示该模型在第7个数据点上存在一个结构断点（虽然显著性不太强）。

sctest.Fstats可以进行supF-, aveF- 和expF检验，即通过遍历方式搜寻断点。例子如下：

## Load dataset "nhtemp" with average yearly temperatures in New Haven
data(nhtemp)
## plot the data
plot(nhtemp)
## test the model null hypothesis that the average temperature remains
## constant over the years for potential break points between 1941
## (corresponds to from = 0.5) and 1962 (corresponds to to = 0.85)
## compute F statistics
fs <- Fstats(nhtemp ~ 1, from = 0.5, to = 0.85)
## plot the F statistics
plot(fs, alpha = 0.01)
## and the corresponding p values
plot(fs, pval = TRUE, alpha = 0.01)
## perform the aveF test
sctest(fs, type = "aveF")

aveF检验显示纽黑文的气温数据存在变化断点，注意这里进行遍历的区间是从0.5到0.85。

supLM检验也可以实现，这里不赘述。

计量检验方法的一个共同短板在于，仅能对时序样本的中间区间进行检验。如果想要对时序数据的拐点进行即时识别乃至预判，则需要寻求其他方法。

参考文献

[1] Chow, Gregory C. "Tests of equality between sets of coefficients in two linear regressions." Econometrica: Journal of the Econometric Society (1960): 591-605.

[2] Andrews, Donald WK. "Tests for parameter instability and structural change with unknown change point." Econometrica: Journal of the Econometric Society (1993): 821-856.

[3] Andrews, Donald WK. "Tests for parameter instability and structural change with unknown change point: A corrigendum." Econometrica (2003): 395-397.

[4] Maasoumi, Esfandiar, Asad Zaman, and Mumtaz Ahmed. "Tests for structural change, aggregation, and homogeneity." Economic Modelling 27, no. 6 (2010): 1382-1391.

[5] Ahmed, Mumtaz, Gulfam Haider, and Asad Zaman. "Detecting structural change with heteroskedasticity." Communications in Statistics-Theory and methods 46, no. 21 (2017): 10446-10455.