张量值张量函数
张量值张量函数有以下类型:标量,向量和高阶张量
标量值张量函数:
Ψ
=
Ψ
(
T
)
=
det
T
Ψ
=
Ψ
(
T
,
S
)
=
T
:
S
\Psi = \Psi(T) =\det T \\ \Psi = \Psi(T,S) =T:S
Ψ=Ψ(T)=detTΨ=Ψ(T,S)=T:S
其中, T , S T, S T,S都是二阶张量
另外,二阶张量值张量函数:
Π
=
Π
(
T
)
=
α
1
+
β
T
\Pi = \Pi(T) = \alpha 1+\beta T
Π=Π(T)=α1+βT
张量级数
函数 f ( x ) f(x) f(x)可以近似表示成Taylor级数: f ( x ) = ∑ i = 0 ∞ 1 n ! ∂ n f ( a ) ∂ x n ( x − a ) n f(x) = \sum_{i=0}^{\infty}\frac{1}{n!}\frac{\partial^nf(a)}{\partial x^n}(x-a)^n f(x)=∑i=0∞n!1∂xn∂nf(a)(x−a)n
那么,对于张量也同样可以推导:假设现在有一个关于二阶张量
E
E
E的标量值张量函数
ψ
(
E
)
\psi(E)
ψ(E),那么可以近似表示成:

关于二阶张量E的二阶张量值张量函数
S
(
E
)
S(E)
S(E),可以近似表示成:
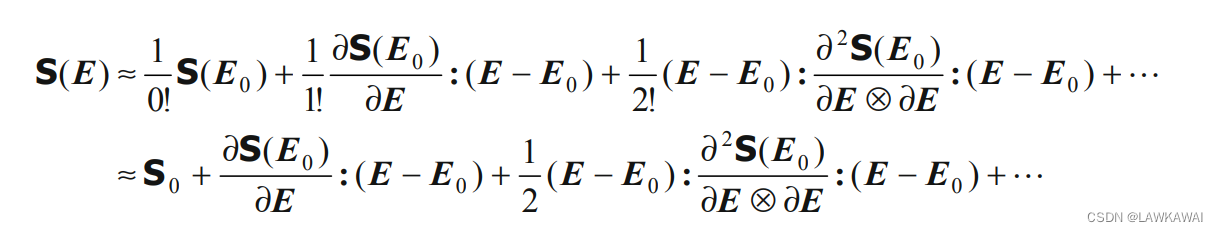
其他代数表达式的级数展开:
exp
S
=
1
+
S
+
1
2
!
S
2
+
1
3
!
S
3
+
.
.
.
ln
(
1
+
S
)
=
S
−
1
2
S
2
+
1
3
S
3
−
.
.
.
sin
(
S
)
=
S
−
1
3
!
S
3
+
1
5
!
S
5
\exp^S = 1+S+\frac{1}{2!}S^2+\frac{1}{3!}S^3+ ...\\ \ln (1+S) = S-\frac{1}{2}S^2+\frac{1}{3}S^3-... \\ \sin (S) = S - \frac{1}{3!}S^3+\frac{1}{5!}S^5
expS=1+S+2!1S2+3!1S3+...ln(1+S)=S−21S2+31S3−...sin(S)=S−3!1S3+5!1S5
参考对称二阶张量
S
S
S的谱表示:
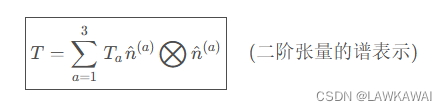
可以将级数表示成:
exp
S
=
∑
a
=
1
3
(
1
+
λ
a
+
1
2
!
λ
a
2
+
1
3
!
λ
a
3
+
.
.
.
)
n
^
(
a
)
⨂
n
^
(
a
)
=
∑
a
=
1
3
exp
λ
a
n
^
(
a
)
⨂
n
^
(
a
)
ln
(
1
+
S
)
=
∑
a
=
1
3
(
λ
a
−
1
2
λ
a
2
+
1
3
λ
a
3
−
.
.
.
)
n
^
(
a
)
⨂
n
^
(
a
)
=
∑
a
=
1
3
ln
(
1
+
λ
a
)
n
^
(
a
)
⨂
n
^
(
a
)
sin
(
S
)
=
∑
a
=
1
3
(
λ
a
−
1
3
!
λ
a
3
+
1
5
!
λ
a
5
+
.
.
.
)
n
^
(
a
)
⨂
n
^
(
a
)
=
∑
a
=
1
3
sin
(
λ
a
)
n
^
(
a
)
⨂
n
^
(
a
)
\exp^S = \sum_{a=1}^3(1+\lambda_a+\frac{1}{2!}\lambda_a^2+\frac{1}{3!}\lambda_a^3+ ...)\hat n^{(a)}\bigotimes \hat n^{(a)}=\sum_{a=1}^3 \exp^{\lambda_a}\hat n^{(a)}\bigotimes \hat n^{(a)}\\ \ln (1+S) = \sum_{a=1}^3(\lambda_a-\frac{1}{2}\lambda_a^2+\frac{1}{3}\lambda_a^3-...) \hat n^{(a)}\bigotimes \hat n^{(a)}=\sum_{a=1}^3\ln(1+\lambda_a)\hat n^{(a)}\bigotimes \hat n^{(a)}\\ \sin (S) = \sum_{a=1}^3(\lambda_a - \frac{1}{3!}\lambda_a^3+\frac{1}{5!}\lambda_a^5+...)\hat n^{(a)}\bigotimes \hat n^{(a)}=\sum_{a=1}^3\sin(\lambda_a)\hat n^{(a)}\bigotimes \hat n^{(a)}
expS=a=1∑3(1+λa+2!1λa2+3!1λa3+...)n^(a)⨂n^(a)=a=1∑3expλan^(a)⨂n^(a)ln(1+S)=a=1∑3(λa−21λa2+31λa3−...)n^(a)⨂n^(a)=a=1∑3ln(1+λa)n^(a)⨂n^(a)sin(S)=a=1∑3(λa−3!1λa3+5!1λa5+...)n^(a)⨂n^(a)=a=1∑3sin(λa)n^(a)⨂n^(a)
其中 λ a \lambda_a λa和 n ^ ( a ) \hat n^{(a)} n^(a)是张量S的特征值和特征向量
各向同性的张量值张量函数
一个二阶张量值的张量函数,
Π
=
Π
(
T
)
\Pi = \Pi(T)
Π=Π(T),如果经过正交变换满足以下条件,则是各向同性的:
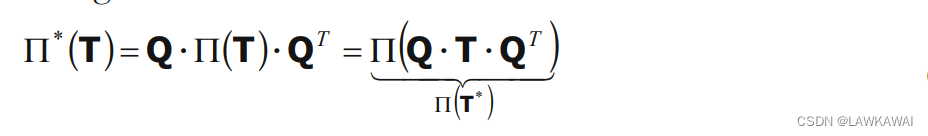
Π
(
T
)
\Pi(T)
Π(T)和
T
T
T有相同的主向量,即
Π
(
T
)
\Pi(T)
Π(T)和
T
T
T是同轴张量。
为了证明这点我们可以先将张量T的分量表示成主空间下的分量:
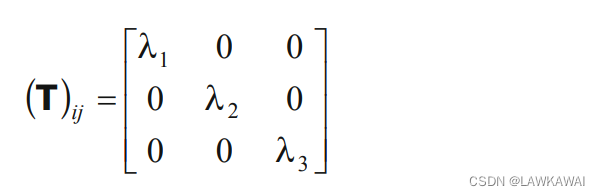
那么由张量T的主不变量构成的张量函数表示为:
Π
=
Π
(
λ
1
,
λ
2
,
λ
3
)
\Pi = \Pi(\lambda_1, \lambda_2, \lambda_3)
Π=Π(λ1,λ2,λ3),以及张量T的变换是:
T
∗
=
Q
⋅
T
⋅
Q
T
T^* = Q \cdot T \cdot Q^T
T∗=Q⋅T⋅QT
同样地,对于张量函数
Π
\Pi
Π的变换,有:
Π
∗
(
T
)
=
Q
⋅
Π
(
T
)
⋅
Q
T
\Pi^*(T) = Q \cdot \Pi(T) \cdot Q^T
Π∗(T)=Q⋅Π(T)⋅QT
假设取正交张量分量为:
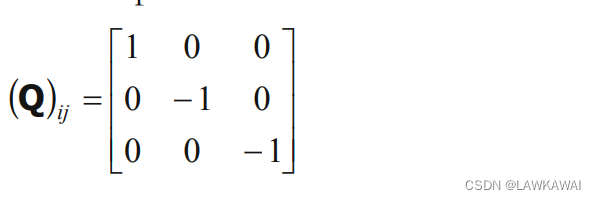
那么,计算得到:

其中,为了满足
Π
∗
=
Π
\Pi^*=\Pi
Π∗=Π(各向同性),必须
Π
12
=
Π
13
=
Π
23
=
0
\Pi_{12}=\Pi_{13}=\Pi_{23}=0
Π12=Π13=Π23=0,因此,
Π
(
T
)
\Pi(T)
Π(T)和
T
T
T有相同的主向量
并且我们可以观察到,一个张量函数当且仅当表示成以下线性变换,才是各向同性的:
Π
=
Π
(
T
)
=
Φ
0
1
+
Φ
1
T
+
Φ
2
T
2
\Pi = \Pi(T) = \Phi_01+\Phi_1T+\Phi_2T^2
Π=Π(T)=Φ01+Φ1T+Φ2T2
其中,
Φ
0
,
Φ
1
,
Φ
2
\Phi_0, \Phi_1, \Phi_2
Φ0,Φ1,Φ2是张量T的不变量或T的特征值。
以下是简单证明。
考虑T和
Π
\Pi
Π的谱表示,分别是:
T
=
∑
a
=
1
3
λ
a
n
^
(
a
)
⨂
n
^
(
a
)
=
λ
1
n
^
(
1
)
⨂
n
^
(
1
)
+
λ
2
n
^
(
2
)
⨂
n
^
(
2
)
+
λ
3
n
^
(
3
)
⨂
n
^
(
3
)
T = \sum_{a=1}^3\lambda_a \hat n^{(a)}\bigotimes \hat n^{(a)} = \lambda_1 \hat n^{(1)}\bigotimes \hat n^{(1)}+ \lambda_2 \hat n^{(2)}\bigotimes \hat n^{(2)}+ \lambda_3 \hat n^{(3)}\bigotimes \hat n^{(3)}
T=a=1∑3λan^(a)⨂n^(a)=λ1n^(1)⨂n^(1)+λ2n^(2)⨂n^(2)+λ3n^(3)⨂n^(3)
Π = ∑ a = 1 3 ω a n ^ ( a ) ⨂ n ^ ( a ) = ω 1 n ^ ( 1 ) ⨂ n ^ ( 1 ) + ω 2 n ^ ( 2 ) ⨂ n ^ ( 2 ) + ω 3 n ^ ( 3 ) ⨂ n ^ ( 3 ) \Pi = \sum_{a=1}^3\omega_a \hat n^{(a)}\bigotimes \hat n^{(a)} = \omega_1 \hat n^{(1)}\bigotimes \hat n^{(1)}+ \omega_2 \hat n^{(2)}\bigotimes \hat n^{(2)}+ \omega_3 \hat n^{(3)}\bigotimes \hat n^{(3)} Π=a=1∑3ωan^(a)⨂n^(a)=ω1n^(1)⨂n^(1)+ω2n^(2)⨂n^(2)+ω3n^(3)⨂n^(3)
有相同的主方向
n
^
(
i
)
\hat n^{(i)}
n^(i),那么可以将以下张量表示成:

求解以上方程组,并且定义
n
^
(
a
)
⨂
n
^
(
a
)
≡
M
(
a
)
\hat n^{(a)}\bigotimes \hat n^{(a)} \equiv M^{(a)}
n^(a)⨂n^(a)≡M(a),可以得到
M
(
a
)
M^{(a)}
M(a)表示成T的函数:
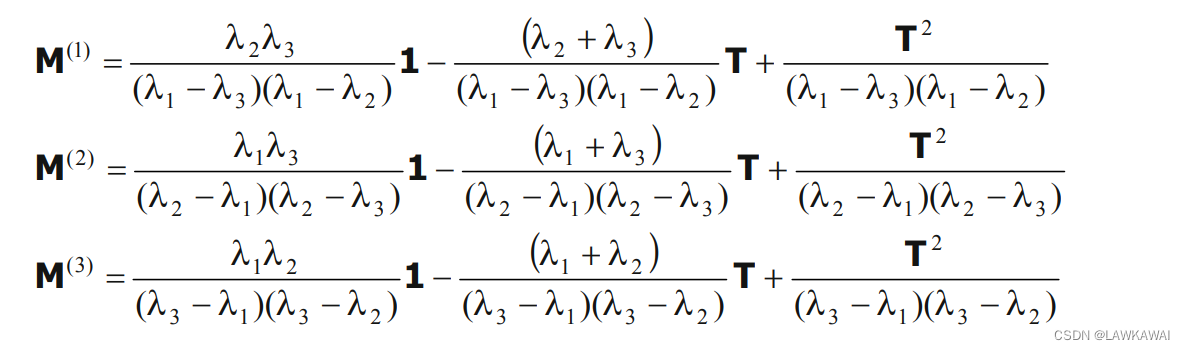
将这个解代入到
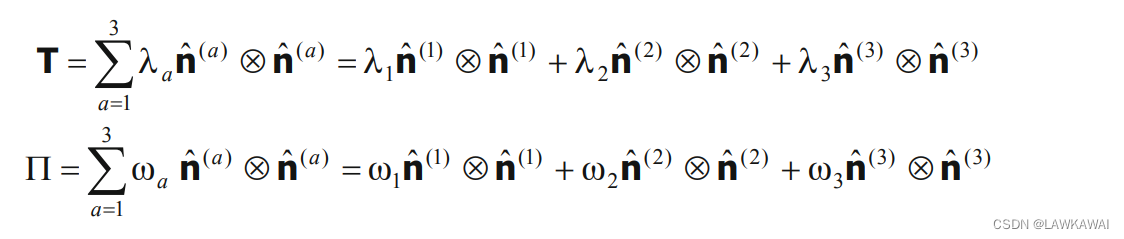
分别得到:
T
=
T
Π
=
Π
(
T
)
=
Φ
0
1
+
Φ
1
T
+
Φ
2
T
2
T = T \\ \Pi = \Pi(T) = \Phi_01+\Phi_1T +\Phi_2T^2
T=TΠ=Π(T)=Φ01+Φ1T+Φ2T2
其中,
Φ
0
,
Φ
1
,
Φ
2
\Phi_0, \Phi_1, \Phi_2
Φ0,Φ1,Φ2分别是T的特征值的函数,为:

同样地,我们可以证明如果给定了一个张量函数
Π
(
T
)
\Pi(T)
Π(T),那么这个张量函数是各向同性的,如果:
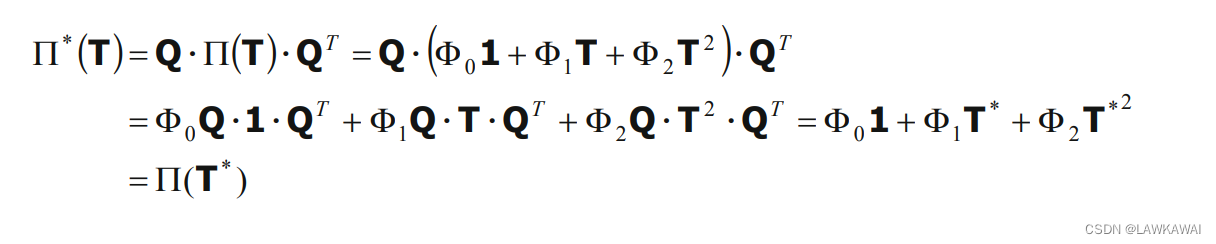
张量值张量函数的导数
先考虑一个标量值的张量函数:
Π
=
Π
(
A
)
\Pi=\Pi(A)
Π=Π(A)
Π
(
A
)
\Pi(A)
Π(A)关于
A
A
A的偏微分是:
∂
Π
∂
A
=
Π
,
A
=
∂
Π
∂
A
i
j
(
e
^
i
⨂
e
^
j
)
\frac{\partial \Pi}{\partial A}=\Pi_{,A}=\frac{\partial \Pi}{\partial A_{ij}}(\hat e_i\bigotimes \hat e_j)
∂A∂Π=Π,A=∂Aij∂Π(e^i⨂e^j)
Π
(
A
)
\Pi(A)
Π(A)的二阶微分是一个四阶张量:
∂
2
Π
∂
A
⨂
∂
A
=
Π
i
,
A
A
=
∂
2
Π
∂
A
i
j
∂
A
k
l
(
e
^
i
⨂
e
^
j
⨂
e
^
k
⨂
e
^
l
)
=
D
i
j
k
l
(
e
^
i
⨂
e
^
j
⨂
e
^
k
⨂
e
^
l
)
\frac{\partial^2 \Pi}{\partial A \bigotimes \partial A}=\Pi_{i,AA}=\frac{\partial^2\Pi}{\partial A_{ij} \partial A_{kl}}(\hat e_i\bigotimes \hat e_j\bigotimes \hat e_k \bigotimes \hat e_l)=D_{ijkl}(\hat e_i\bigotimes \hat e_j\bigotimes \hat e_k \bigotimes \hat e_l)
∂A⨂∂A∂2Π=Πi,AA=∂Aij∂Akl∂2Π(e^i⨂e^j⨂e^k⨂e^l)=Dijkl(e^i⨂e^j⨂e^k⨂e^l)
令
C
C
C和b是正定对称二阶张量:
C
=
F
T
⋅
F
;
b
=
F
⋅
F
T
C = F^T \cdot F; \quad b = F \cdot F^T
C=FT⋅F;b=F⋅FT
其中F是任意的二阶张量,且
det
F
>
0
\det F >0
detF>0,我们必须牢记的是,有一个标量值的各向同性张量函数
Φ
=
Φ
(
I
C
,
I
I
C
,
I
I
I
C
)
\Phi=\Phi(I_C, II_C, III_C)
Φ=Φ(IC,IIC,IIIC),表示成C的主不变量,其中
I
C
=
I
b
,
I
I
C
=
I
I
b
,
I
I
I
C
=
I
I
I
b
I_C = I_b, II_C=II_b, III_C=III_b
IC=Ib,IIC=IIb,IIIC=IIIb
接下来,我们求出
Φ
\Phi
Φ关于C和b的偏导数,我们先需要验证以下关系:
F
⋅
Φ
,
C
⋅
F
T
=
Φ
,
b
⋅
b
F \cdot \Phi_{,C}\cdot F^T=\Phi_{,b}\cdot b
F⋅Φ,C⋅FT=Φ,b⋅b
那么,通过应用导数的链式法则,我们可以得到:
Φ , C = ∂ Φ ( I C , I I C , I I I C ) ∂ C = ∂ Φ ∂ I C ∂ I C ∂ C + ∂ Φ ∂ I I C ∂ I I C ∂ C + ∂ Φ ∂ I I I C ∂ I I I C ∂ C \Phi_{,C} =\frac{\partial \Phi(I_C, II_C, III_C)}{\partial C}=\frac{\partial\Phi}{\partial I_C}\frac{\partial I_C}{\partial C} +\frac{\partial\Phi}{\partial II_C}\frac{\partial II_C}{\partial C} +\frac{\partial\Phi}{\partial III_C}\frac{\partial III_C}{\partial C} Φ,C=∂C∂Φ(IC,IIC,IIIC)=∂IC∂Φ∂C∂IC+∂IIC∂Φ∂C∂IIC+∂IIIC∂Φ∂C∂IIIC
考虑主不变量的偏导数,有:

将以上式子代入到
Φ
,
C
\Phi_{,C}
Φ,C里面,得到:
Φ
,
C
=
∂
Φ
∂
I
C
1
+
∂
Φ
∂
I
I
C
(
I
C
1
−
C
)
+
∂
Φ
∂
I
I
I
C
(
I
I
I
C
C
−
1
)
\Phi_{,C} =\frac{\partial \Phi}{\partial I_C}1+\frac{\partial\Phi}{\partial II_C}(I_C1-C) +\frac{\partial\Phi}{\partial III_C}(III_CC^{-1})
Φ,C=∂IC∂Φ1+∂IIC∂Φ(IC1−C)+∂IIIC∂Φ(IIICC−1)
整理一下:
Φ
,
C
=
(
∂
Φ
∂
I
C
+
∂
Φ
∂
I
I
C
I
C
)
1
−
(
∂
Φ
∂
I
I
C
)
C
+
(
∂
Φ
∂
I
I
I
C
I
I
I
C
)
C
−
1
\boxed{\Phi_{,C} =(\frac{\partial \Phi}{\partial I_C }+\frac{\partial\Phi}{\partial II_C}I_C)1-(\frac{\partial\Phi}{\partial II_C})C +(\frac{\partial\Phi}{\partial III_C}III_C)C^{-1}}
Φ,C=(∂IC∂Φ+∂IIC∂ΦIC)1−(∂IIC∂Φ)C+(∂IIIC∂ΦIIIC)C−1
另一种表达形式:
将
∂
I
C
∂
C
=
1
,
∂
I
I
C
∂
C
=
I
C
1
−
C
,
∂
I
I
I
C
∂
C
=
C
2
−
I
C
C
+
I
I
C
1
\frac{\partial I_C}{\partial C}=1, \quad \frac{\partial II_C}{\partial C}=I_C1-C, \quad \frac{\partial III_C}{\partial C}=C^2-I_CC+II_C1
∂C∂IC=1,∂C∂IIC=IC1−C,∂C∂IIIC=C2−ICC+IIC1代入到
Φ
,
C
=
∂
Φ
(
I
C
,
I
I
C
,
I
I
I
C
)
∂
C
=
∂
Φ
∂
I
C
∂
I
C
∂
C
+
∂
Φ
∂
I
I
C
∂
I
I
C
∂
C
+
∂
Φ
∂
I
I
I
C
∂
I
I
I
C
∂
C
\Phi_{,C} =\frac{\partial \Phi(I_C, II_C, III_C)}{\partial C}=\frac{\partial\Phi}{\partial I_C}\frac{\partial I_C}{\partial C} +\frac{\partial\Phi}{\partial II_C}\frac{\partial II_C}{\partial C} +\frac{\partial\Phi}{\partial III_C}\frac{\partial III_C}{\partial C}
Φ,C=∂C∂Φ(IC,IIC,IIIC)=∂IC∂Φ∂C∂IC+∂IIC∂Φ∂C∂IIC+∂IIIC∂Φ∂C∂IIIC
我们可以得到:
Φ
,
C
=
(
∂
Φ
∂
I
C
+
∂
Φ
∂
I
I
C
I
C
+
∂
Φ
∂
I
I
I
C
I
I
C
)
1
−
(
∂
Φ
∂
I
I
C
+
∂
Φ
∂
I
I
I
C
I
C
)
C
+
(
∂
Φ
∂
I
I
I
C
)
C
2
\boxed{\Phi_{,C} =(\frac{\partial \Phi}{\partial I_C }+\frac{\partial\Phi}{\partial II_C}I_C+\frac{\partial \Phi}{\partial III_C}II_C)1-(\frac{\partial\Phi}{\partial II_C}+\frac{\partial \Phi}{\partial III_C}I_C)C +(\frac{\partial\Phi}{\partial III_C})C^{2}}
Φ,C=(∂IC∂Φ+∂IIC∂ΦIC+∂IIIC∂ΦIIC)1−(∂IIC∂Φ+∂IIIC∂ΦIC)C+(∂IIIC∂Φ)C2
如果我们再次将 ∂ I C ∂ C = 1 , ∂ I I C ∂ C = I I C C − 1 − I I I C C − 2 , ∂ I I I C ∂ C = I I I C C − 1 \frac{\partial I_C}{\partial C}=1, \quad \frac{\partial II_C}{\partial C}=II_C C^{-1}-III_C C^{-2}, \quad \frac{\partial III_C}{\partial C}=III_C C^{-1} ∂C∂IC=1,∂C∂IIC=IICC−1−IIICC−2,∂C∂IIIC=IIICC−1
可以得到:
Φ
,
C
=
(
∂
Φ
∂
I
C
)
1
+
(
∂
Φ
∂
I
I
C
I
I
C
+
∂
Φ
∂
I
I
I
C
I
I
I
C
)
C
−
1
−
(
∂
Φ
∂
I
I
C
I
I
I
C
)
C
−
2
\boxed{\Phi_{,C} =(\frac{\partial \Phi}{\partial I_C })1+(\frac{\partial\Phi}{\partial II_C}II_C+\frac{\partial\Phi}{\partial III_C}III_C)C^{-1}-(\frac{\partial\Phi}{\partial II_C}III_C )C^{-2}}
Φ,C=(∂IC∂Φ)1+(∂IIC∂ΦIIC+∂IIIC∂ΦIIIC)C−1−(∂IIC∂ΦIIIC)C−2
如果有
I
C
=
I
b
,
I
I
C
=
I
I
b
,
I
I
I
C
=
I
I
I
b
I_C = I_b, II_C = II_b, III_C = III_b
IC=Ib,IIC=IIb,IIIC=IIIb,则有:
Φ
,
b
=
(
∂
Φ
∂
I
b
+
∂
Φ
∂
I
I
b
I
b
)
1
−
∂
Φ
∂
I
I
b
b
+
∂
Φ
∂
I
I
I
b
I
I
I
b
b
−
1
\boxed{\Phi_{,b}=(\frac{\partial \Phi}{\partial I_b}+\frac{\partial \Phi}{\partial II_b}I_b)1-\frac{\partial \Phi}{\partial II_b}b+\frac{\partial \Phi}{\partial III_b}III_b b^{-1}}
Φ,b=(∂Ib∂Φ+∂IIb∂ΦIb)1−∂IIb∂Φb+∂IIIb∂ΦIIIbb−1
利用
Φ
,
C
=
(
∂
Φ
∂
I
C
+
∂
Φ
∂
I
I
C
I
C
)
1
−
(
∂
Φ
∂
I
I
C
)
C
+
(
∂
Φ
∂
I
I
I
C
I
I
I
C
)
C
−
1
\boxed{\Phi_{,C} =(\frac{\partial \Phi}{\partial I_C }+\frac{\partial\Phi}{\partial II_C}I_C)1-(\frac{\partial\Phi}{\partial II_C})C +(\frac{\partial\Phi}{\partial III_C}III_C)C^{-1}}
Φ,C=(∂IC∂Φ+∂IIC∂ΦIC)1−(∂IIC∂Φ)C+(∂IIIC∂ΦIIIC)C−1
可以得到:
F
⋅
Φ
,
C
⋅
F
T
=
(
∂
Φ
∂
I
C
+
∂
Φ
∂
I
I
C
I
C
)
F
⋅
1
⋅
F
T
−
∂
Φ
∂
I
I
C
F
⋅
C
⋅
F
T
+
∂
Φ
∂
I
I
I
C
I
I
I
C
F
⋅
C
−
1
⋅
F
T
F \cdot \Phi_{,C}\cdot F^T = (\frac{\partial \Phi}{\partial I_C}+\frac{\partial \Phi}{\partial II_C}I_C)F\cdot 1\cdot F^T-\frac{\partial \Phi}{\partial II_C}F\cdot C \cdot F^T+\frac{\partial \Phi}{\partial III_C}III_CF \cdot C^{-1} \cdot F^T
F⋅Φ,C⋅FT=(∂IC∂Φ+∂IIC∂ΦIC)F⋅1⋅FT−∂IIC∂ΦF⋅C⋅FT+∂IIIC∂ΦIIICF⋅C−1⋅FT
然后,我们可以观察到:

所以,
F
⋅
Φ
,
C
⋅
F
T
F \cdot \Phi_{,C} \cdot F^T
F⋅Φ,C⋅FT可以重写成:
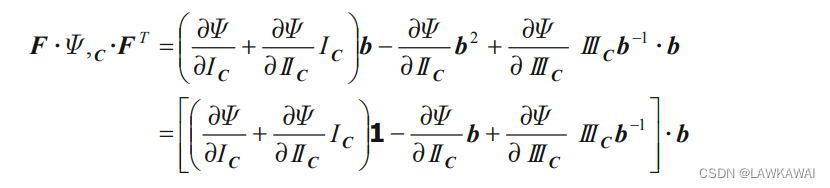
根据
Φ
,
b
=
(
∂
Φ
∂
I
b
+
∂
Φ
∂
I
I
b
I
b
)
1
−
∂
Φ
∂
I
I
b
b
+
∂
Φ
∂
I
I
I
b
I
I
I
b
b
−
1
\boxed{\Phi_{,b}=(\frac{\partial \Phi}{\partial I_b}+\frac{\partial \Phi}{\partial II_b}I_b)1-\frac{\partial \Phi}{\partial II_b}b+\frac{\partial \Phi}{\partial III_b}III_b b^{-1}}
Φ,b=(∂Ib∂Φ+∂IIb∂ΦIb)1−∂IIb∂Φb+∂IIIb∂ΦIIIbb−1 和上式,可以得到:
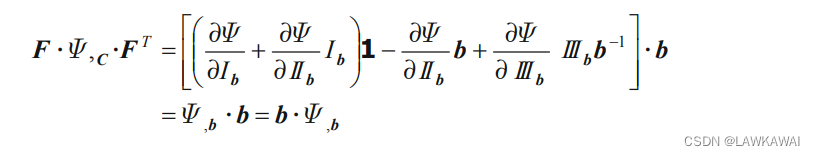
这表示,
Φ
,
C
\Phi_{,C}
Φ,C和b是同轴张量
再次,根据
C
=
F
T
⋅
F
C = F^T \cdot F
C=FT⋅F,计算标量值张量函数
Φ
=
Φ
(
C
)
\Phi = \Phi(C)
Φ=Φ(C)的关于张量F的导数:

张量C关于F的导数如下所示:
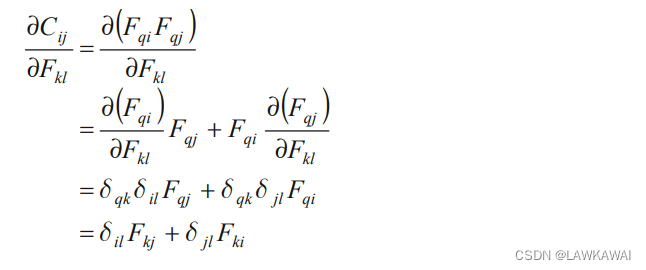
将以上的张量C关于F的导数代入到张量函数
Φ
(
C
)
\Phi(C)
Φ(C)关于张量F的导数表达式中: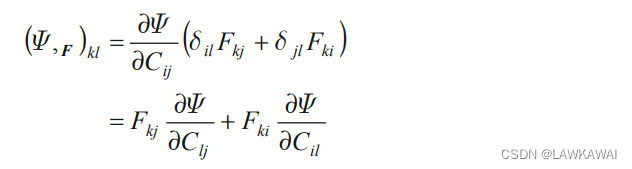 由于C的对称性,
C
i
j
=
C
j
i
C_{ij} = C_{ji}
Cij=Cji,可以得到:
由于C的对称性,
C
i
j
=
C
j
i
C_{ij} = C_{ji}
Cij=Cji,可以得到:

现在,假设C由对称二阶张量U给出,
C
=
U
T
⋅
U
=
U
⋅
U
=
U
2
C = U^T\cdot U=U \cdot U=U^2
C=UT⋅U=U⋅U=U2,那么
Φ
,
C
\Phi_{,C}
Φ,C为:
Φ
,
C
=
2
Φ
,
C
⋅
U
=
2
U
⋅
Φ
,
C
\Phi_{,C} = 2\Phi_{,C}\cdot U=2U\cdot \Phi_{,C}
Φ,C=2Φ,C⋅U=2U⋅Φ,C
因此,可以说
Φ
,
C
\Phi_{,C}
Φ,C和U是同轴张量
令A是对称二阶张量,
Φ
=
Φ
(
A
)
\Phi = \Phi(A)
Φ=Φ(A)是一个标量值张量函数,那么一下关系成立:
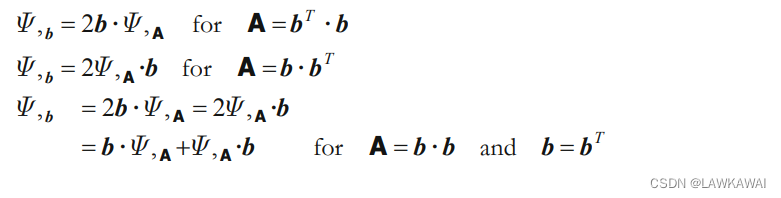
参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics