1数据结构
1.1常量与变量
变量命名第一个字符必须为字母，变量可以由数字、字母、下划线组成，区分大小写。
常量：
1.2 数值型数据
双精度：64位 智能存储15位左右十进制数 double()
单精度 ：32位，single（）
常用于图像表示与处理：unit8(),8位
1.3 符号型数据
转换为符号型：sym(A)
显示符号变量的任意精度：vpa(A),vpa(A,n)
显示符号变量的属性：assumptions()
设置符号变量的属性：assume()
通过sym(),可以把双精度的数转换为符号型的数
例如：
将20位数据输入双精度表示不了，只能以符号型输入：
>> A=sym(12345678901234567890)
A =
12345678901234567168
可以看出后三位错误，以双精度输入不可行
采取以符号型输入
>> A=sym('1234567890123456789')
A =
1234567890123456789
2 矩阵与向量输入
2.1 基本语句结构
直接赋值语句
加;不显示运算结果
例1，输入实数矩阵
A=[1 2 3; 4 5 6; 7 8 10]
A1=[1,2,3;4,5,6;7,8,10]
A2=inv(A) '求逆矩阵'
A =
1 2 3
4 5 6
7 8 10
A1 =
1 2 3
4 5 6
7 8 10
A2 =
-0.6667 -1.3333 1.0000
-0.6667 3.6667 -2.0000
1.0000 -2.0000 1.0000
动态定维：给现有矩阵增加一行：
A3=[A;[1 2 3]]
A3 =
1 2 3
4 5 6
7 8 10
1 2 3
给现有矩阵增加一列：
A4=[A3,[1;2;3;4]]
A4 =
1 2 3 1
4 5 6 2
7 8 10 3
1 2 3 4
例2，复数矩阵输入
>> B=[1+2i 2+3i 3+4i;4+5i 5+6i 6+7i;7+8i 8+9i 9+10i]
B =
1.0000 + 2.0000i 2.0000 + 3.0000i 3.0000 + 4.0000i
4.0000 + 5.0000i 5.0000 + 6.0000i 6.0000 + 7.0000i
7.0000 + 8.0000i 8.0000 + 9.0000i 9.0000 +10.0000i
函数调用
一般的函数对应一个.m文件
2.2 冒号表达式与子矩阵提取
冒号表达式：
例：
v1=0:0.2:pi '在0-π之间以0.2位步长生成数据'
v1 =
1 至 8 列
0 0.2000 0.4000 0.6000 0.8000 1.0000 1.2000 1.4000
9 至 16 列
1.6000 1.8000 2.0000 2.2000 2.4000 2.6000 2.8000 3.0000
>> v1a=linspace(0,pi,50)'0-π之间取50个点生成行向量，包括端点值'
v1a =
1 至 8 列
0 0.0641 0.1282 0.1923 0.2565 0.3206 0.3847 0.4488
9 至 16 列
0.5129 0.5770 0.6411 0.7053 0.7694 0.8335 0.8976 0.9617
17 至 24 列
1.0258 1.0899 1.1541 1.2182 1.2823 1.3464 1.4105 1.4746
25 至 32 列
1.5387 1.6029 1.6670 1.7311 1.7952 1.8593 1.9234 1.9875
33 至 40 列
2.0517 2.1158 2.1799 2.2440 2.3081 2.3722 2.4363 2.5005
41 至 48 列
2.5646 2.6287 2.6928 2.7569 2.8210 2.8851 2.9493 3.0134
49 至 50 列
3.0775 3.1416
子矩阵提取
例：
A =
1 2 3
4 5 6
7 8 0
>> B=A(1:2:end,:) '按行提取，间隔一行提取一行，提取其行所对应的所有列，也就是提取A中所有的奇数行'
B =
1 2 3
7 8 0
>> C=A([1 1 1 1],:) '提取A中的第一行重复4次'
C =
1 2 3
1 2 3
1 2 3
1 2 3
3 矩阵的代数运算
3.1 矩阵的转置运算
对于复数来说 共轭这直接转置不同，对实数矩阵来说二者完全一致。
共轭转置
C=A’
直接转置
C=A.’
3.2 加减法、乘法、除法、乘方
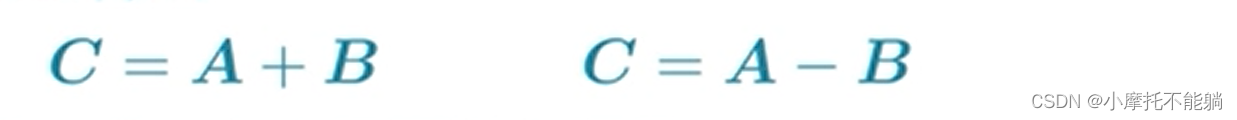
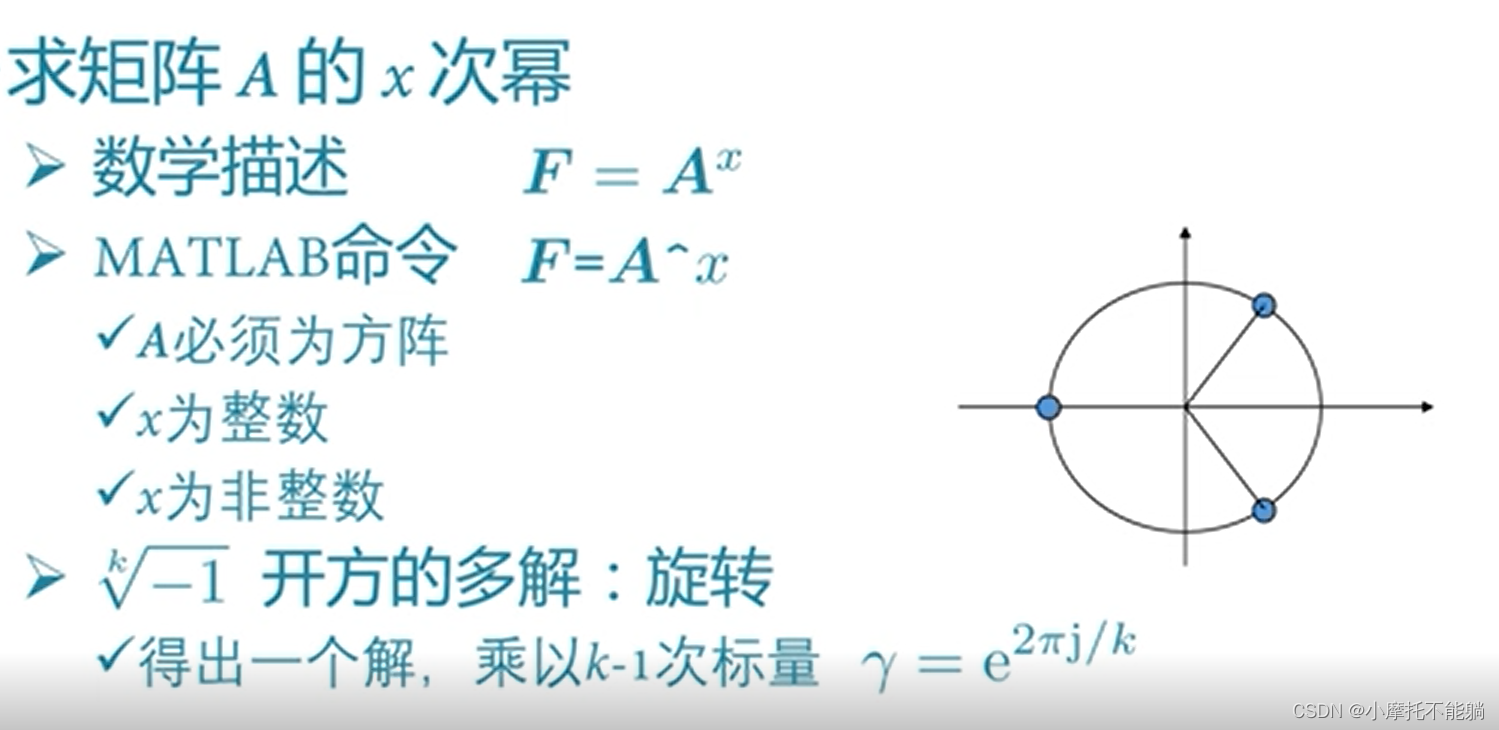
3.3 点运算
矩阵相应元素之间的运算
4 矩阵的其它运算
4.1逻辑运算
4.2 比较运算
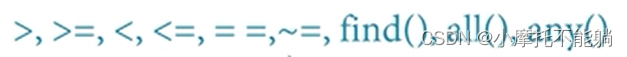
4.3 解析结果的化简与变换
simplify()：化简公式
>> syms s;p=(s+3)^2*(s^2+3*s+2)*(s^3+12*s^2+48*s+64)
p =
(s + 3)^2*(s^2 + 3*s + 2)*(s^3 + 12*s^2 + 48*s + 64)
>> p1=simplify(p)
p1 =
(s + 3)^2*(s + 4)^3*(s^2 + 3*s + 2)
因式分解：
>> p3=factor(p),p4=prod(p3)
p3 =
[ s + 3, s + 3, s + 2, s + 1, s + 4, s + 4, s + 4]
p4 =
(s + 1)*(s + 2)*(s + 3)^2*(s + 4)^3
4.4 变量替换
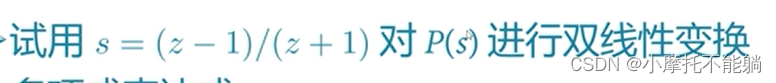`>> syms s;p=(s+3)2*(s2+3s+2)(s3+12*s2+48*s+64)
p =
(s + 3)2*(s2 + 3s + 2)(s^3 + 12s^2 + 48s + 64)
syms s z;
p1=simplify(subs(p,s,(z-1)/(z+1)))
p1 =
(8z(2z + 1)^2(3z + 1)(5*z + 3)^3)/(z + 1)^7`
4.5 Hibert矩阵
A=hilb(3)
[n,d]=rat(A) %n是分子矩阵，d是分母矩阵
A =
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
n =
1 1 1
1 1 1
1 1 1
d =
1 2 3
2 3 4
3 4 5
4.6 最大公约数与最小公倍数
m=1856120;
n=1483720;
gcd(m,n) %最大公约数
lcm(m,n) %最小公倍数
factor(lcm(m,n))%质因数分解
ans =
1960
ans =
1.4051e+09
ans =
2 2 2 5 7 7 757 947
4.7 找出某个范围内的全部质数
isprime()如果是质数将返回1 不是返回0
>> a=1:100;b=a(isprime(a))
b =
1 至 11 列
2 3 5 7 11 13 17 19 23 29 31
12 至 22 列
37 41 43 47 53 59 61 67 71 73 79
23 至 25 列
83 89 97
4.8 全排列计算
prems()
>> p=perms(1:4),size(p)
p =
4 3 2 1
4 3 1 2
4 2 3 1
4 2 1 3
4 1 3 2
4 1 2 3
3 4 2 1
3 4 1 2
3 2 4 1
3 2 1 4
3 1 4 2
3 1 2 4
2 4 3 1
2 4 1 3
2 3 4 1
2 3 1 4
2 1 4 3
2 1 3 4
1 4 3 2
1 4 2 3
1 3 4 2
1 3 2 4
1 2 4 3
1 2 3 4
ans =
24 4
5 流程结构
5.1 循环结构
for结构
while结构
例子：
求解1-100的和
s1=0;
for i =1:100
s1=s1+i;
end
s1
s1 =
5050
例子：
s=0;m=0;
while(s<=10000),
m=m+1;
s=s+m;
end
s,m
s =
10011
m =
141
例子：向量化编程
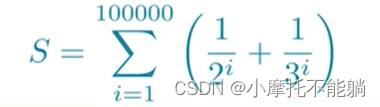
i=1:100000; s=sum(1./2.^i+1./3.^i); s
s =
1.5000
5.2 转移结构
条件转移结构
开关结构
![C++ 类和对象下 [补充]](https://img-blog.csdnimg.cn/bdd44515e9544534a3428eb699961d46.png)
