完全背包

教程视频：https://www.bilibili.com/video/BV1uK411o7c9
这里基于背包理论基础介绍。

完全背包问题概述

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

例题

背包最大重量为4。
物品为：

物品	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

每件商品都有无限个！ 问背包能背的物品最大价值是多少？

01背包和完全背包唯一不同就是体现在遍历顺序上，这里直接针对遍历顺序经行分析！
为了保证每件物品仅使用一次，内层for循环遍历背包容量时需要倒序遍历（不能改变上次循环的结果）。

for(int i=0;i<weight.length;i++){
	for(int j=bagSize;j>=weight[i];j--){
		dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
	}
}

而完全背包的物品是可以添加多次的，所以仅需将内层for循环转化为正序遍历，即可多次使用物品i。

for(int i=0;i<weight.length;i++){
	for(int j= weight[i];j<=bagSize;j++){
		dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
	}
}

此时，dp状态转移图如下所示：
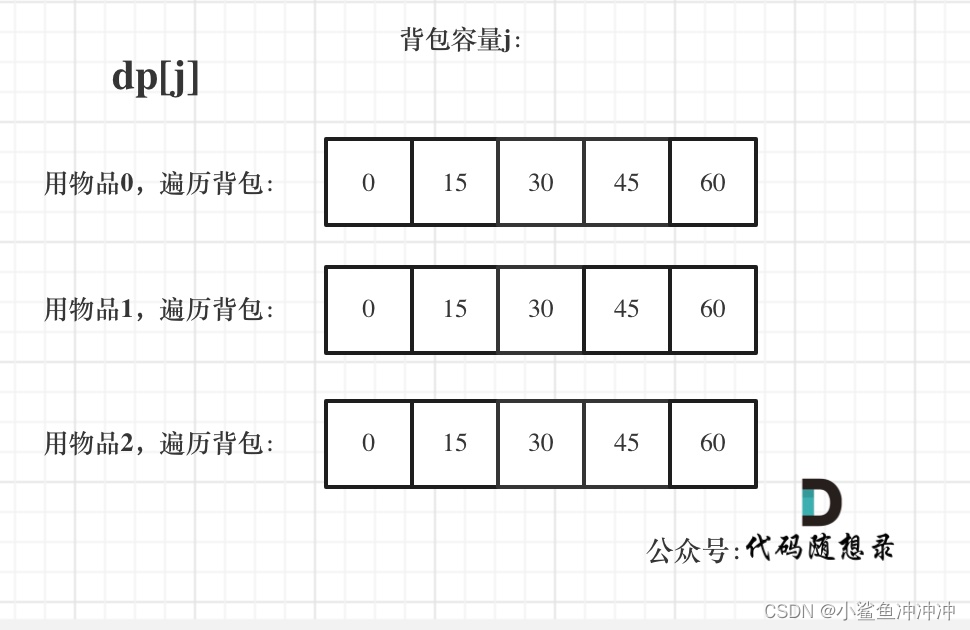在这里插入图片描述题解代码：

//先遍历物品，再遍历背包
private static void testCompletePack(){
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWeight = 4;
    int[] dp = new int[bagWeight + 1];
    for (int i = 0; i < weight.length; i++){ // 遍历物品
        for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    for (int maxValue : dp){
        System.out.println(maxValue + "   ");
    }
}

//先遍历背包，再遍历物品
private static void testCompletePackAnotherWay(){
    int[] weight = {1, 3, 4};
    int[] value = {15, 20, 30};
    int bagWeight = 4;
    int[] dp = new int[bagWeight + 1];
    for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
        for (int j = 0; j < weight.length; j++){ // 遍历物品
            if (i - weight[j] >= 0){
                dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
            }
        }
    }
    for (int maxValue : dp){
        System.out.println(maxValue + "   ");
    }
}

遍历顺序分析

在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序是无所谓的！
从递推公式dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);可以看出，dp[j] 是根据下标j之前所对应的dp[j]计算出来的。因此，只要保证下标j之前的dp[j]都是计算出了值即可。

先遍历物品再遍历背包时，dp状态转移如下：
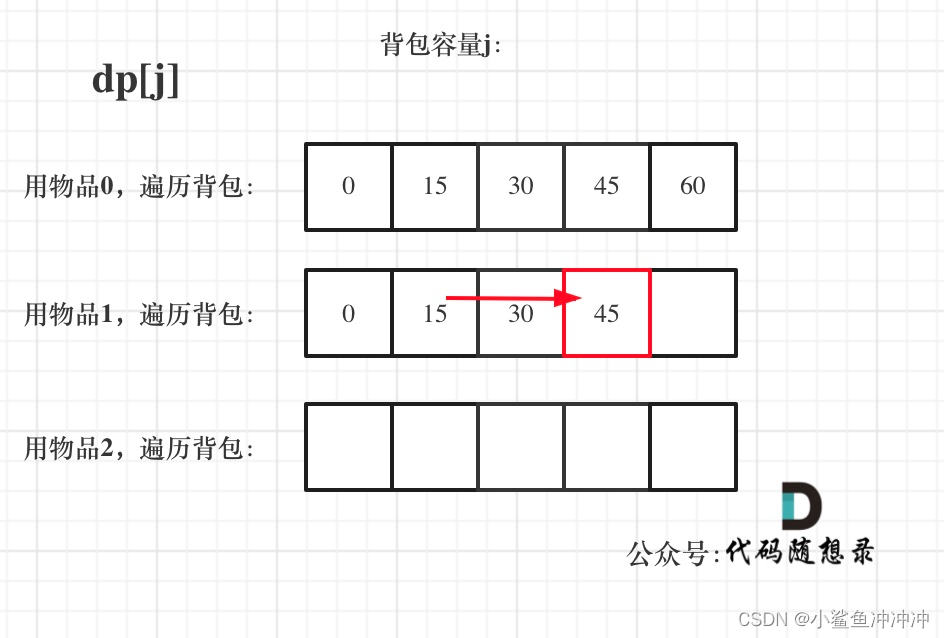
在这里插入图片描述

先遍历背包再遍历物品时，dp状态转移如下：
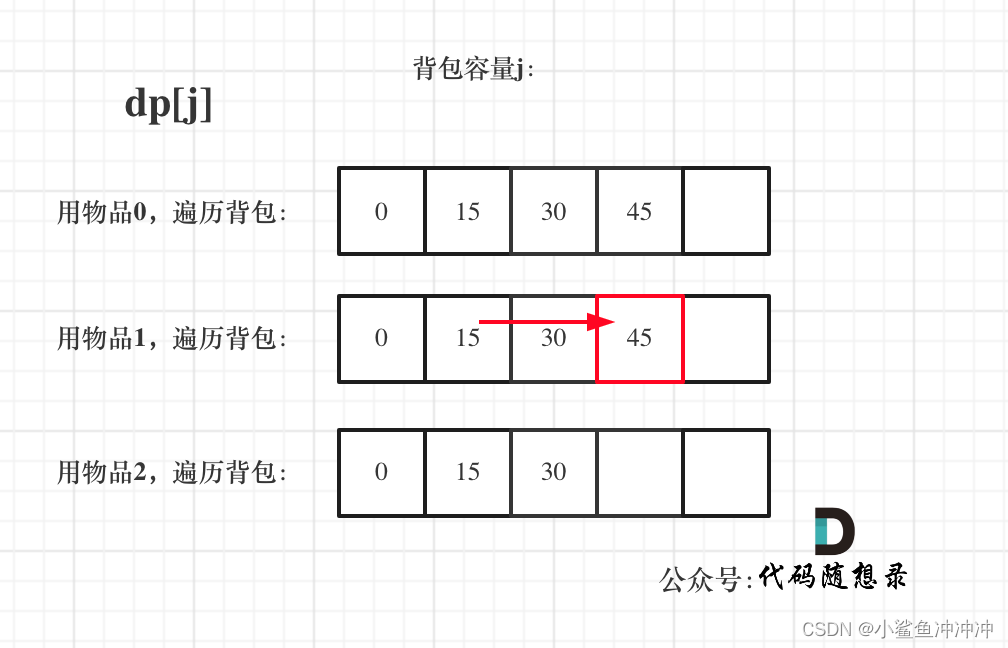
在这里插入图片描述
这两个图可以得出，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值。（但是没必要这样做，容易出错且仅适用与纯完全背包问题）

518. 零钱兑换 II

教程视频：https://www.bilibili.com/video/BV1KM411k75j/?spm_id_from=pageDriver&vd_source=ddffd51aa532d23e6feac69924e20891
在这里插入图片描述

思路：
1、dp[j]含义：能够凑成 j 金额的硬币组合数（在0～i种硬币中取）
2、递推公式：dp[j] = dp[j]+dp[j-coins[i]];思考过程类似 494. 目标和
3、dp初始化：dp[0]=1;其他下标初始化为0。
4、遍历顺序：外层for遍历硬币，内层for正序遍历总金额（这里是求组合种类数）
5、打印验证

解法一：动态规划

class Solution {
    public int change(int amount, int[] coins) {
        int[] dp = new int[amount+1];
        dp[0]=1;
        for(int i=0;i<coins.length;i++){
            for(int j=coins[i];j<=amount;j++){
                dp[j]=dp[j]+dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
}

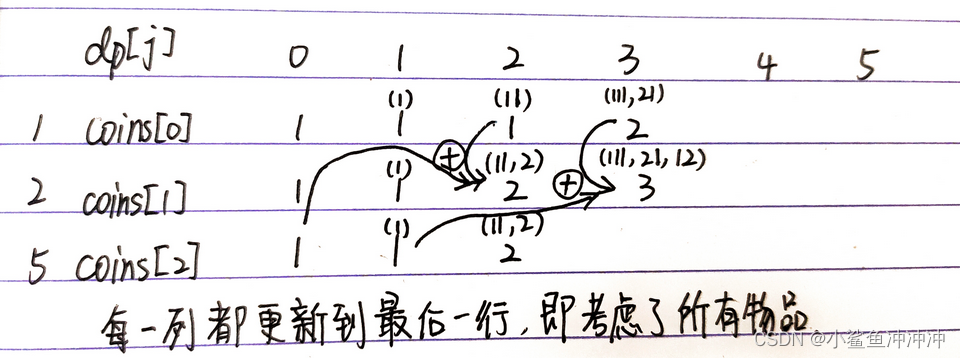
本题遍历顺序深入剖析：
入下入dp状态转移图所示，如果先遍历背包容量，后遍历物品，则会考虑顺序，变成求排列种类。
在这里插入图片描述

377. 组合总和 Ⅳ

教程视频：https://www.bilibili.com/video/BV1V14y1n7B6/?spm_id_from=pageDriver&vd_source=ddffd51aa532d23e6feac69924e20891
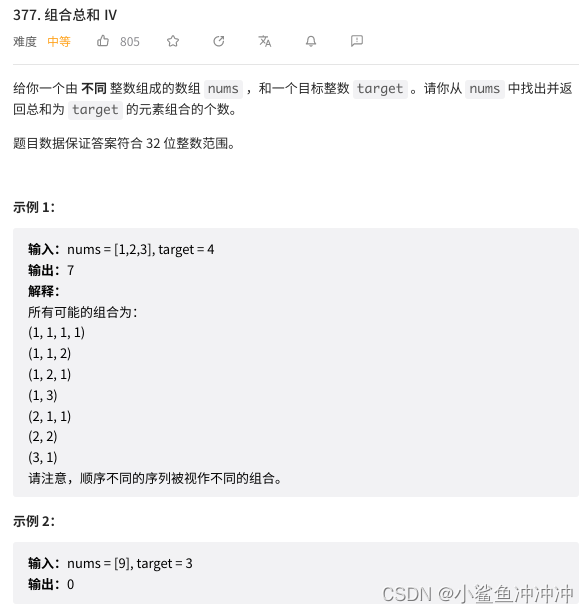
在这里插入图片描述

思路：
1、dp[j]含义：能够凑成 j 目标的元素排列数（在0～i种硬币中取）
2、递推公式：dp[j]+=dp[j-nums[i]];思考过程类似 494. 目标和
3、dp初始化：dp[0]=1;其他下标初始化为0。
4、遍历顺序：外层for正序遍历背包容量，内层for遍历物品（这里是求排列种类数）
5、打印验证

解法一：动态规划

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target+1];
        dp[0]=1;
        for(int j=1;j<=target;j++){
            for(int i=0;i<nums.length;i++){
                if(j>=nums[i]){
                    dp[j]+=dp[j-nums[i]];
                }
            }
        }
        return dp[target];
    }
}