本章的代码实现基于上一篇BST与优先队列的基类进行平衡二叉树，即AVL树。

AVL的概念

总所周知，BST在插入数据随机的情况下，其搜索能达到O(logn)的性能，但如果插入数据有序，或是经过若干次的插入与删除，BST将会退化，甚至变为线性的链表，这不利于搜索。
如何保持BST的优秀查找性质，同时又不至于过分的维护成本（例如完全二叉树），AVL树就是其中一个答案。
AVL树通过维护左右子树高度差，从而保证了搜索的效率，AVL的定义如下：

1. AVL树要么是空树，那么满足以下两个条件
2. AVL树的左右子树也是AVL树
3. AVL节点的平衡因子绝对值不超过1，平衡因子(balance factor)定义：左右子树高度差=左子树高度-右子树高度

AVL查询效率

AVL树的查询效率同样为O(logn)，具体证明如下:
使用数学归纳法，假设高度为h的AVL树，其所能容纳的最少节点数为N(h)(即容纳N个节点时，AVL最大即最糟糕的高度)，可以发现满足以下情况：

1. h=1时，N(h)=1
2. h=2时，N(h)=2
3. 当h>=3时，最糟糕的树必然根节点BF不为0(因为BF=0时，左右子树都高h-1，容纳节点必然多与1个h-2子树+1个h-1子树)，那么此时最糟糕的树= 1个根节点 + 1个h-1的子树 + 1个h-2的子树，即N(h)= 1 + N(h-1) + N(h-2)
4. 令G(h)=N(h)+1,则G(h)=F(h+2)，F为斐波那契数列，而随着i的增大，斐波那契数列有一个性质：$$\frac{F_i}{F_{i-1}}\to \frac{\sqrt{5}+1}{2}=\Phi$$
5. 可以估算i较大时，$$F_i\approx \frac{{\Phi }^i}{\sqrt{5}}$$$$N_h=F_{h+2}-1=\frac{{\Phi }^{h+2}}{\sqrt{5}}-1$$$$h=\frac{log{N}_h+1-2log\Phi +\frac{1}{2}log5}{log\Phi }\approx 1.44log{N}_h+C$$
6. 故得证AVL的搜索效率为O(logn)，在最糟糕的情况下，其搜索效率仅为完全二叉树的1.44倍，退化性能不多。

AVL的插入

AVL的查找与BST完全一致，因此无需赘述，较为困难的是AVL的插入与删除，因为必须维护AVL的平衡因子，因此涉及BF的更新与树的旋转。
再进一步之前，我们需要意识到以下几点：

1. AVL是递归定义的，AVL的左右子树都是AVL树
2. 上一条性质意味着，如果一个节点失衡，只会影响局部而不一定是整体。那么通过调整局部的子树，可以达到整体的平衡
3. 树的旋转前后，如果不改变树的高度，那么子树平衡的同时不影响父节点的BF，说明调整完毕，否则需要继续递归向上调整

1.插入节点

插入节点与BST一致，唯一的区别在于，AVL树我们使用了三叉链和bF，需要注意parent节点的连接与bF的默认置零。

void insert(int key)
{
    TreeNode* cur = this->root;
    TreeNode* pre = cur;
    TreeNode* node = new TreeNode(key);
    //利用pre和cur找到插入的位置
    while (cur)
    {
        pre = cur;
        if (key < cur->val)
            cur = cur->left;
        else
            cur = cur->right;
    }
    //根节点
    if (this->root == nullptr)
    {
        this->root = node;
        return;
    }
    //在左边
    if (key < pre->val)
        pre->left = node;
    //右边
    else
        pre->right = node;
    node->parent = pre;
    cur = node;
    //.......
}

2.更新平衡因子BF

当我们插入一个新的节点时，必然会影响父节点的BF值，如果改变了父节点的高度，则会影响组父节点的BF，因此我们必须向上溯源更新BF值，更新原则如下：

• 若插入的值key < 溯源节点pre，说明新节点位于pre的左子树，左子树高度增大，pre->bF++
• 若插入的值key > 溯源节点pre，说明新节点位于pre的右子树，右子树高度增大，pre->bF–

现在我们考虑更新后的pre的平衡因子bF，从而判断是否继续向上溯源，分析如下：

1. 首先明确，根据AVL的定义，更新前pre的bF可能取值为-1,0,1
2. 若更新后bF为0，说明更新前为-1或1，且新节点插入了较低的子树，插入较低子树意味着pre的高度不变，无需继续溯源，插入完成，跳出循环
3. 若更新后bF为-1或1，说明更新前为0，两子树高度一致，在插入新节点后，其中一颗子树高度增大，因此pre的高度发生变化，需要继续溯源，pre=pre->parent,直到根节点为止。
4. 若更新后bF为-2或2，说明更新前为-1或1，且新节点插入了较高的子树，此时，pre失衡，且pre为失衡的最小子树，需要进行旋转调整，因为insert造成的失衡可以通过1次旋转完成调整，并且使pre的BF=0，因此跳出循环，进入旋转模块。

void insert(int key)
{
    //......
    //上接插入节点
    bool unbanlance = false;
    //更新bF值
    while (pre)
    {
        //沿着搜索路径向上回溯，修改bF
        if (key < pre->val)
            ++pre->bF;
        else
            --pre->bF;
        //平衡
        if (pre->bF == 0)
            return;
        //pre处失衡
        else if (pre->bF == 2 || pre->bF == -2)
        {
            unbanlance = true;
            break;
        }
        //继续向上调整
        else
        {
            cur = pre;
            pre = pre->parent;
        }
    }
    //......
}

3.旋转调整树的结构

调整树的结构，我们可以对失衡情况进行分类，共有以下4类。

3.1 LL 右旋

如图所示：

LL代表着这样一种情况：

• 插入前，P节点的BF为1，L节点的BF为0（必然是这种情况，不可能P为1且L为1，否则P不是最先找到节点），代表着P的左子树比后子树高1，L的左右子树一致
• 插入后，L和P的左子树高度增加1，P节点的BF为2，L节点的BF为1。此时P节点失衡，我们采用右旋，下降P节点，上升L节点。
• 右转后，L和P节点的BF值都归0

//a为失衡节点，b为a的左节点
void LL(TreeNode* a, TreeNode* b)
{
    a->left = b->right;
    if (b->right != nullptr)
        b->right->parent = a;
    b->right = a;
    b->parent = a->parent;
    a->parent = b;
    a->bF = 0;
    b->bF = 0;
    if (b->parent==nullptr)
        this->root = b;
    else if (b->val < b->parent->val)
        b->parent->left = b;
    else
        b->parent->right = b;
}

3.2 RR 左旋

如图所示：

RR对应着LL的对称情况，不必多说。

//a为失衡节点，b为a的右节点
void RR(TreeNode* a, TreeNode* b)
{
    bool isRoot = a->parent == nullptr;
    a->right = b->left;
    if (b->left != nullptr)
        b->left->parent = a;
    b->left = a;
    b->parent = a->parent;
    a->parent = b;
    a->bF = 0;
    b->bF = 0;
    if (b->parent == nullptr)
        this->root = b;
    else if (b->val < b->parent->val)
        b->parent->left = b;
    else
        b->parent->right = b;
}

3.3 LR 左右双旋

如图所示：

LR对应着这一种情况：

• 插入前，与LL的情况一致。
• 插入后，L的右子树高度增加1，而P的左子树高度增加1，P节点的BF为2，L节点的BF为-1，所需要进行的调整较为复杂，但可以拆分为两步进行。
• 首先对L、LR进行一次左旋，下降L，上升LR。之后对P、LR进行一次右旋，下降P，上升LR。
• 左右双旋后，LR的BF=0，而L和P的BF则需要根据插入节点所位于LR的位置进行判断（也可根据LR之前的BF进行判断），如果插入在LR的左子树，则L->BF=0,P->BF=-1，插在LR的右子树，则L->BF=1,P->BF=0

//a为失衡节点，b为a的左节点
void LR(TreeNode* a, TreeNode* b)
{
    TreeNode* c = b->right;
    b->right = c->left;
    a->left = c->right;
    if (c->left != nullptr)
        c->left->parent = b;
    if (c->right != nullptr)
        c->right->parent = a;
    c->left = b;
    c->right = a;
    c->parent = a->parent;
    b->parent = c;
    a->parent = c;
    //c就是插入节点
    if (c->bF == 0)
    {
        a->bF = 0;
        b->bF = 0;
    }
    //插入节点在c的左子树
    else if (c->bF = 1)
    {
        b->bF = 0;
        a->bF = -1;
    }
    else
    {
        b->bF = 1;
        a->bF = 0;
    }
    c->bF = 0;
    if (c->parent == nullptr)
        this->root = c;
    else if (c->val < c->parent->val)
        c->parent->left = c;
    else
        c->parent->right = c;
}

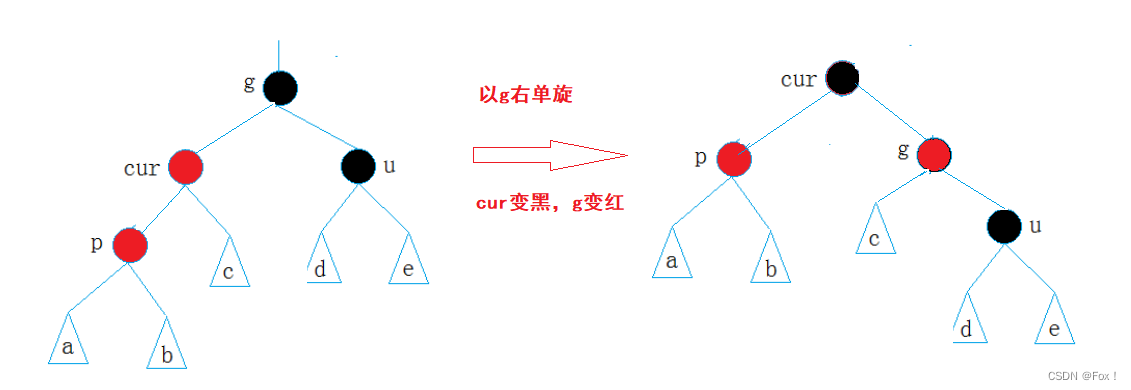
3.4 RL 右左双旋

如图所示：

RL对应着LR的对称情况，不必多说。

//a为失衡节点，b为a的右节点
void RL(TreeNode* a, TreeNode* b)
{
    TreeNode* c = b->left;
    b->left = c->right;
    a->right = c->left;
    if (c->right != nullptr)
        c->right->parent = b;
    if (c->left != nullptr)
        c->left->parent = a;

    c->left = a;
    c->right = b;
    c->parent = a->parent;
    a->parent = c;
    b->parent = c;

    if (c->bF == 0)
    {
        a->bF = 0;
        b->bF = 0;
    }
    else if (c->bF = 1)
    {
        a->bF = 0;
        b->bF = -1;
    }
    else
    {
        a->bF = 1;
        b->bF = 0;
    }
    c->bF = 0;
    if (c->parent == nullptr)
        this->root = c;
    else if (c->val < c->parent->val)
        c->parent->left = c;
    else
        c->parent->right = c;
}

4 插入总结

最后我们对插入做一个总结，具体过程如下：

1. 首先，从根节点出发，找到新插入节点的位置（空节点）和其父节点
2. 插入节点
3. 从插入节点的父节点开始，向上回溯更新BF
4. 若是更新后的BF=1或-1，则继续更新，直到根节点为止；若是更新后的BF=0，则插入结束，返回；若是更新后的BF=2或-2，则找到了最小的失衡AVL子树，跳出循环，修复该子树。
5. 若是失衡，则根据失衡节点a和插入节点所在分支的子节点b的BF值，判断是LL/RR/LR/RL中哪种情况，并进行相应的旋转操作。

完整代码如下:

//插入
void insert(int key)
{
    TreeNode* cur = this->root;
    TreeNode* pre = cur;
    TreeNode* node = new TreeNode(key);
    //利用pre和cur找到插入的位置
    while (cur)
    {
        pre = cur;
        if (key < cur->val)
            cur = cur->left;
        else
            cur = cur->right;
    }
    //根节点
    if (this->root == nullptr)
    {
        this->root = node;
        return;
    }
    //在左边
    if (key < pre->val)
        pre->left = node;
    //右边
    else
        pre->right = node;
    node->parent = pre;
    cur = node;
    bool unbanlance = false;
    //更新bF值
    while (pre)
    {
        //沿着搜索路径向上回溯，修改bF
        if (key < pre->val)
            ++pre->bF;
        else
            --pre->bF;
        //平衡
        if (pre->bF == 0)
            return;
        //pre处失衡
        else if (pre->bF == 2 || pre->bF == -2)
        {
            unbanlance = true;
            break;
        }
        //继续向上调整
        else
        {
            cur = pre;
            pre = pre->parent;
        }
    }
    //失衡状态需要调整
    if (unbanlance)
    {
        //LL型
        if (pre->bF == 2 && cur->bF == 1)
            LL(pre, cur);
        else if (pre->bF == 2 && cur->bF == -1)
            LR(pre, cur);
        else if (pre->bF == -2 && cur->bF == -1)
            RR(pre, cur);
        else
            RL(pre, cur);
    }
    return;
}

AVL的删除

相比于插入，AVL的删除实际上可能更加困难，正如BST的删除也比插入更难。
与BST一致，我们依然是从叶节点、单边节点和双边节点开始考虑。

1.寻找删除节点

我们删除节点的流程应为：找到并记录删除节点->更新BF值->调整树结构->实际删除节点。

• 无删除节点，返回
• 叶节点，记录下该节点和父节点
• 单边节点，记录下该节点和父节点
• 双边节点，采用替换删除法，采用前驱（左子树最大值）或后继（右子树最小值）替换该删除节点的值，实际删除节点为前驱或后继节点，本程序采用后继，记录下后继节点和父节点。
• 删除节点是叶节点或单边节点，同时是根节点的情况，需要特殊处理。(双边节点实际上删的是后继节点，所以不需要单独处理)

void remove(int key)
{
    TreeNode* cur = this->root;
    TreeNode* pre = nullptr;
    TreeNode* deleteNode = nullptr;
    TreeNode* deleteParent = nullptr;
    while (cur)
    {
        if (key > cur->val)
        {
            pre = cur;
            cur = cur->right;
        }
        else if (key < cur->val)
        {
            pre = cur;
            cur = cur->left;
        }
        //找到了需要删除的节点
        else
        {
            //需要删除节点的左子树为空
            if (cur->left == nullptr)
            {
                //若是根节点，将右子树作为新的根节点即可
                //根节点没有父节点，无需更新bF
                if (cur->parent == nullptr)
                {
                    root = cur->right;
                    if (root)
                        root->parent = nullptr;
                    delete(cur);
                    return;
                }
                else
                {
                    //记录信息
                    deleteNode = cur;
                    deleteParent = pre;
                }
            }
            else if (cur->right == nullptr)
            {
                if (cur->parent == nullptr)
                {
                    root = cur->left;
                    if (root)
                        root->parent = nullptr;
                    delete(cur);
                    return;
                }
                else
                {
                    deleteNode = cur;
                    deleteParent = pre;
                }
            }
            else
            {
                //左右子树都非空，进行替换，并且更新需要删除的位置
                //利用rightMin进行更新
                TreeNode* minRight = cur->right;
                while (minRight->left)
                    minRight = minRight->left;
                //替换
                cur->val = minRight->val;
                //标记删除节点
                deleteNode = minRight;
                deleteParent = minRight->parent;
            }
            break;
        }
    }

    //没有需要删除的节点
    if (deleteParent == nullptr)
        return;
    //.......
}

2.更新平衡因子BF + 旋转

不同于插入，在删除之中，旋转可能会改变树的高度，因此更新BF和旋转必须在一个循环中反复进行，不能拆分进行。

毫无疑问，我们依然需要确立更新原则，更新原则如下：

• 若删除的节点 < 溯源节点deleteParent，说明删除节点位于deleteParent的左子树，左子树高度减小，deleteParent->bF–
• 若删除的节点 > 溯源节点deleteParent，说明删除节点位于deleteParent的右子树，右子树高度增孝，deleteParent->bF++

现在我们考虑更新后的deleteParent的平衡因子bF，从而判断是否继续向上溯源，分析如下：

1. 依然明确，根据AVL的定义，更新前deleteParent的bF可能取值为-1,0,1
2. 若更新后bF为0，说明更新前为-1或1，删除了较高子树的节点，继续向上回溯。
3. 若更新后bF为-1或1，说明更新前为0，两子树高度一致，删除其中一棵子树的节点，树的高度没有发生边海，至此插入结束。
4. 若更新后bF为-2或2，说明更新前为-1或1，且删除了较低子树的节点，此时，deleteParent失衡，需要进行旋转调整，旋转调整分为6种情况，其中4种情况会改变树的高度，需要继续向上回溯。

以下为失衡时的6种情况，以及对应的处理方法：

1. 当deleteParent的平衡因子BF为2，deleteParent的左孩子平衡因子为1时，即降低了R节点的树高，与插入时的LL情况一致，采用右旋，旋转前的子树路径为P->L->L的左子树，高度为1+1+h，旋转后的子树路径为L->L的左子树，高度为1+h，右子树为L->P->(L右子树h-1)或(P右子树h-1)，高度由h+2→h+1，必须继续回溯。
2. 当deleteParent的平衡因子BF为2，deleteParent的左孩子平衡因子为-1时，即降低了R节点的树高，与插入时的LR情况一致，采用左右双旋，同上进行分析，高度h+2→h+1，继续回溯。
3. 当deleteParent的平衡因子BF为2，deleteParent的左孩子平衡因子为0时，此时情况较为特殊，降低了R的树高，但是L的两个子树高度一致，这是插入中没有的情况，我们采用右旋+改变平衡因子调整方法的方法进行，右旋后，将L->BF=-1,P->BF=1，旋转前后的高度h+2→h+1，高度没有变化，不需要继续回溯
4. 当deleteParent的平衡因子BF为-2，deleteParent的左孩子平衡因子为-1时，第1种情况的对称情况，左旋，继续回溯。
5. 当deleteParent的平衡因子BF为-2，deleteParent的左孩子平衡因子为1时，第2种情况的对称情况，右左双旋，继续回溯
6. 当deleteParent的平衡因子BF为-2，deleteParent的左孩子平衡因子为0时，第3种情况的对称情况，左旋+改变平衡因子调整方法，将R->BF=1,P->BF=-1，不需要继续回溯。

void remove(int key)
{
    //.....
    //上接寻找删除节点
    //备份
    TreeNode* delP = deleteParent;
    TreeNode* del = deleteNode;
    //更新bF
    while (deleteParent)
    {
        //删除左子树
        if (deleteNode->val < deleteParent->val)
            --deleteParent->bF;
        else
            ++deleteParent->bF;
        //根据bF进一步判断
        //bF=0，说明原来为-1 或者 1，此时改变了树的高度，需要继续向上更新
        if (deleteParent->bF == 0)
        {
            deleteNode = deleteParent;
            deleteParent = deleteParent->parent;
        }
        //bF=1 / -1，说明原来为0，此时没有修改树的高度（高度由最高的子树决定），不需要继续更新
        else if (deleteParent->bF == 1 || deleteParent->bF == -1)
        {
            break;
        }
        //bF=2 / -2，失衡，需要进行旋转
        else
        {
            //左边子树高
            if (deleteParent->bF == 2)
            {
                //LL情况
                if (deleteParent->left->bF == 1)
                    LL(deleteParent, deleteParent->left);
                //LR
                else if (deleteParent->left->bF == -1)
                    LR(deleteParent, deleteParent->left);
                else
                {
                    //由于右子树的降低而导致的失衡，左节点的两个子树高度一致
                    //可以采用LL进行处理，但需要重新调整bF
                    LL(deleteParent, deleteParent->left);
                    //调整deleteNode和左子节点如今的位置
                    deleteParent = deleteParent->parent;
                    //旋转前，左子树=1节点+2个节点的子树AB（高h） 高h+1；右子树=1个子树C（高h-1） 高h-1
                    //旋转后，左子树=子树A 高h，右子树=原来根节点 + 左子树B（高h）+右子树C（高h-1） 高h+1
                    //因此，新的根节点左子树低于右子树，右节点的子树则是左子树高于右子树
                    deleteParent->bF = -1;
                    deleteNode->right->bF = 1;
                    //此时，树的高度没有发生变化，不需要继续向上更新，故break
                    break;
                }
            }
            else
            {
                //RR
                if (deleteParent->right->bF == -1)
                    RR(deleteParent, deleteParent->right);
                //RL
                else if (deleteParent->right->bF == 1)
                    RL(deleteParent, deleteParent->right);
                else
                {
                    RR(deleteParent, deleteParent->right);
                    deleteParent = deleteParent->parent;
                    deleteParent->bF = 1;
                    deleteParent->left->bF = -1;
                    break;
                }
            }

            //旋转会调整树的高度，需要继续更新（不需要更新的情况已经break了）
            deleteNode = deleteParent;
            deleteParent = deleteParent->parent;
        }
    }
    //......
}

3.实际删除节点

利用备份好的删除节点信息，考虑单边节点和删除节点所位于的子树情况进行删除。

void remove(int key)
{
    //.....
    //上接bf调整和旋转
    //删除节点（必然有一颗子树为空）
    //删除节点的左子树为空
    if (del->left == nullptr)
    {
        //删除节点位于左子树
        if (del->val < delP->val)
            delP->left = del->right;
        else
            delP->right = del->right;
        if (del->right != nullptr)
            del->right->parent = delP;
    }
    //右子树为空
    else
    {
        if (del->val < delP->val)
            delP->left = del->left;
        else
            delP->right = del->left;
        //此时delteNode->left必然不为nullptr（这种情况已经讨论过）
        del->left->parent = delP;
    }
    delete(del);
    return;
}

4.删除总结

相比于插入，删除需要注意的情况更多，且存在旋转改变高度，上层父节点也需要旋转的可能。
在此就不再列删除流程，而是记录一些关键点：

1. 对于删除的节点种类的选择：叶节点、单边节点、双边节点，双边采用替换删除法转为叶节点或单边节点
2. 更新BF和旋转树需要同时在循环内进行，循环停止条件为不改变树高度或到达根节点
3. 不改变树高度分为删除本身不改变和旋转后恢复删除前高度两种情况，后者只在父节点的BF=2或-2，且子节点BF=0时出现

总体代码如下：

void remove(int key)
{
    TreeNode* cur = this->root;
    TreeNode* pre = nullptr;
    TreeNode* deleteNode = nullptr;
    TreeNode* deleteParent = nullptr;
    while (cur)
    {
        if (key > cur->val)
        {
            pre = cur;
            cur = cur->right;
        }
        else if (key < cur->val)
        {
            pre = cur;
            cur = cur->left;
        }
        //找到了需要删除的节点
        else
        {
            //需要删除节点的左子树为空
            if (cur->left == nullptr)
            {
                //若是根节点，将右子树作为新的根节点即可
                //根节点没有父节点，无需更新bF
                if (cur->parent == nullptr)
                {
                    root = cur->right;
                    if (root)
                        root->parent = nullptr;
                    delete(cur);
                    return;
                }
                else
                {
                    //记录信息
                    deleteNode = cur;
                    deleteParent = pre;
                }
            }
            else if (cur->right == nullptr)
            {
                if (cur->parent == nullptr)
                {
                    root = cur->left;
                    if (root)
                        root->parent = nullptr;
                    delete(cur);
                    return;
                }
                else
                {
                    deleteNode = cur;
                    deleteParent = pre;
                }
            }
            else
            {
                //左右子树都非空，进行替换，并且更新需要删除的位置
                //利用rightMin进行更新
                TreeNode* minRight = cur->right;
                while (minRight->left)
                    minRight = minRight->left;
                //替换
                cur->val = minRight->val;
                //标记删除节点
                deleteNode = minRight;
                deleteParent = minRight->parent;
            }
            break;
        }
    }

    //没有需要删除的节点
    if (deleteParent == nullptr)
        return;

    //备份
    TreeNode* delP = deleteParent;
    TreeNode* del = deleteNode;
    //更新bF
    while (deleteParent)
    {
        //删除左子树
        if (deleteNode->val < deleteParent->val)
            --deleteParent->bF;
        else
            ++deleteParent->bF;
        //根据bF进一步判断
        //bF=0，说明原来为-1 或者 1，此时改变了树的高度，需要继续向上更新
        if (deleteParent->bF == 0)
        {
            deleteNode = deleteParent;
            deleteParent = deleteParent->parent;
        }
        //bF=1 / -1，说明原来为0，此时没有修改树的高度（高度由最高的子树决定），不需要继续更新
        else if (deleteParent->bF == 1 || deleteParent->bF == -1)
        {
            break;
        }
        //bF=2 / -2，失衡，需要进行旋转
        else
        {
            //左边子树高
            if (deleteParent->bF == 2)
            {
                //LL情况
                if (deleteParent->left->bF == 1)
                    LL(deleteParent, deleteParent->left);
                //LR
                else if (deleteParent->left->bF == -1)
                    LR(deleteParent, deleteParent->left);
                else
                {
                    //由于右子树的降低而导致的失衡，左节点的两个子树高度一致
                    //可以采用LL进行处理，但需要重新调整bF
                    LL(deleteParent, deleteParent->left);
                    //调整deleteNode和左子节点如今的位置
                    deleteParent = deleteParent->parent;
                    //旋转前，左子树=1节点+2个节点的子树AB（高h） 高h+1；右子树=1个子树C（高h-1） 高h-1
                    //旋转后，左子树=子树A 高h，右子树=原来根节点 + 左子树B（高h）+右子树C（高h-1） 高h+1
                    //因此，新的根节点左子树低于右子树，右节点的子树则是左子树高于右子树
                    deleteParent->bF = -1;
                    deleteNode->right->bF = 1;
                    //此时，树的高度没有发生变化，不需要继续向上更新，故break
                    break;
                }
            }
            else
            {
                //RR
                if (deleteParent->right->bF == -1)
                    RR(deleteParent, deleteParent->right);
                //RL
                else if (deleteParent->right->bF == 1)
                    RL(deleteParent, deleteParent->right);
                else
                {
                    RR(deleteParent, deleteParent->right);
                    deleteParent = deleteParent->parent;
                    deleteParent->bF = 1;
                    deleteParent->left->bF = -1;
                    break;
                }
            }

            //旋转会调整树的高度，需要继续更新（不需要更新的情况已经break了）
            deleteNode = deleteParent;
            deleteParent = deleteParent->parent;
        }
    }

    //删除节点（必然有一颗子树为空）
    //删除节点的左子树为空
    if (del->left == nullptr)
    {
        //删除节点位于左子树
        if (del->val < delP->val)
            delP->left = del->right;
        else
            delP->right = del->right;
        if (del->right != nullptr)
            del->right->parent = delP;
    }
    //右子树为空
    else
    {
        if (del->val < delP->val)
            delP->left = del->left;
        else
            delP->right = del->left;
        //此时delteNode->left必然不为nullptr（这种情况已经讨论过）
        del->left->parent = delP;
    }
    delete(del);
    return;
}

总结

总算把AVL树的博客写完了，我发现大量的博客确实缺少了对于AVL删除的叙述，有些可惜。
之后的红黑树、B树、B+树、哈夫曼树，估计不会自己实现，而是记录一下思路和细节，也没有必要再费劲地去处理红黑树N多种情况。
——2023.5.17