问:CART决策树可以有多个分支结构。
答:错误。CART决策树每个内部节点只能有两个分支结构,这些分支分别对应于二进制判定的是或否。因此,CART决策树的每个节点将数据集分成两个较小的子集,其中一个子集满足某种特定条件,而另一个子集不满足该条件。
决策树
决策树是一种基本的分类与回归的算法,其模型呈树形结构,在分类问题种,表示基于特征对实例进行分类的过程,可以认为是if-then规则的集合,也可以认为是定义在特征空间与类空间上的条件概率分布
分类与回归一个比较浅层的区别是回归针对连续变量,分类针对离散变量
在学习的时候,利用训练数据,根据损失函数最小化原则建立决策树模型。
在预测的时候,对新的数据,利用决策树模型进行分类
决策树的学习通常包括3个步骤:特征选择、决策树的生成、决策树的剪枝
决策树学习思想主要来自ID3算法、C4.5算法以及CART算法
CART决策树
CART全称为(classification and regression tree),即分类回归树模型,其决策树模型可应用与分类也可应用于回归
分类: 离散
回归: 连续
1.分类树
因为每次选择该特征中一个取值对该特征进行二分
与ID3使用信息增益不同,CART分类树生成算法使用基尼指数选择最优特征和决定该特征的最优切分点
1.1 基尼系数
基尼系数公式的定义如下:


1.1 特征离散
如果特征是离散的,那么它就是按照特征的可选值进行划分节点,该特征有几个离散值,那么就划分成几个节点,和ID3、C4.5决策树一样。
1.2 特征连续
如果特征值是连续的,划分节点时就不能够按照特征的可选数量进行分割节点,因为连续特征有很多可选值,所以肯定不能和离散特征一样的分割方式,它是采用二叉树的方式,每次按照连续特征分成两个分支,分割方式为将待分割特征的所有值从小到大排序,然后选中其中一个值作为划分点,将样本划分为两个部分。
比如说,有一列特征A,值为 [ 1 , 5 , 2 , 6 , 8 , 3 ] 按照顺序进行排序,[ 1 , 2 , 3 , 5 , 6 , 8 ] ,所以可选的值很多,我们假设选中3作为划分点,将原始样本划分为:[ 1 , 2 , 3 ] 和 [ 5 , 6 , 8 ] 。

按照连续型特征分割后然后在用基尼系数进行评估。
2.回归树
其实回归树就是标签为连续型的,所以此时不能够使用基尼系数、熵这种的概率评估作为评估指标,因为不是分类不能够利用古典概型求出概率,所以我们考虑使用均方误差作为特征划分的好坏,将划分后的每个节点所有样本的均方误差之和之前没划分的节点的均方误差做差来代替基尼系数。
之前分类问题是计算所有特征的信息增益,此时我们会计算每个特征按照每个划分点的均方误差: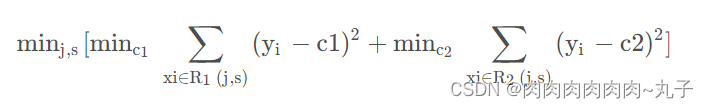
上面的j是不同的特征,s是对应每个特征可供选择的划分点,因为一个连续特征的值很多,所以划分点很多,要选择最优的。
括号内的意思就是找出针对特征j的最优划分点s,采用均方误差,最外层是特征,计算不同特征。
回归的比分类相对麻烦一些,分类只需要计算每个特征的信息增益,回归是计算每个特征的均方误差增益,但是它多了一个步骤就是求每个特征增益的时候还要找出最优划分值s。
这样生成的树成为最小二乘回归树。
三、剪枝算法