1.概率图模型：HMM（隐马）,MEMM（最大熵）,CRF（条件随机场）
概率：既然是一个图那么就是一个有圈有边的结构，圈代表随机向量，随机变量之间有边，边上有概率
既然是模型肯定可以求解：
有向图求解方式：p(Y)=p(x1)*p(x2|x1)....
无向图求解方式：
z(x)：代表归一化因子，作用就是为了把最终结果，缩放成一个概率
累乘：图中有几个最大团，就累乘多少次
势函数：指数函数：e的多少次方：特征函数
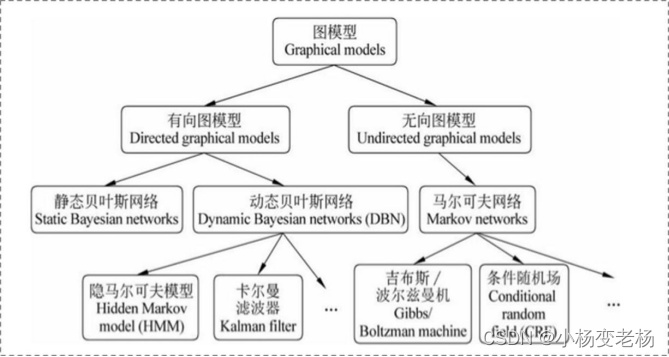
图模型：
1.有向图：有箭头，表示单向依赖关系
2.无向图：没有箭头，表示双向依赖关系
有向图：
1.静态贝叶斯网络
2.动态贝叶斯网络
无向图：
马尔可夫网络
团的概念：由几个节点所构成的闭环。（且节点之间相互连接）
最大团：最多有几个元素构成一个闭环并且相互连接（节点之间相互连接）
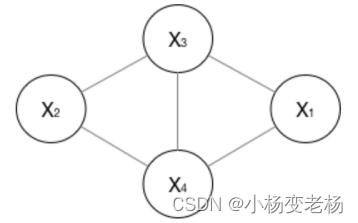
两个最大团：
x1,x3,x4;x2,x3,x4
2.齐次马尔可夫假设：
当前这个状态只依赖于前一个状态。相当于学习过的n-gram的n=2
3.生成式模型和判别式模型
学习的过程不一样
如何体现学习方式不同：建模不同，那么学习方式就不同。
生成式模型：可以直接生成模型来判别
生成式模型求得联合概率分布P(Y,X)，对于没有见过的X，你要求出X与不同标记之间的联合概率分布
判别式模型：只有规律，通过某些特征进行判别
1.对条件概率分布P(Y|X)建模
2.对所有的样本只构建一个模型，确认总体判别边界
3.观测到输入什么特征，就预测最可能的label
4.另外，判别式的优点是：对数据量要求没生成式的严格，速度也会快，小数据量下准确率也会好些。
4.序列标注：词性标注、命名实体识别、搜狗输入法
之前的学习解决四大类问题：回归,分类,聚类,降维
序列标注问题和分类问题的区别和联系
序列标注是一类特殊的分类任务，分类问题就不用细说了，标注问题相当于是分类问题的一个拓展，
分类是输入一个序列得到一个分类结果，而标注问题，输入的是一个序列，输出的也是一个序列，
标注问题输出的是一个向量，分类问题输出的是一个标签。
概率图：
在概率图模型中，数据通过公式G（V，E）进行建模表示：
V：代表的就是随机变量，它可以是一个token同时也可以是一个label，具体的由Y=（y1,y2,y3......yn）为随机变量建模，需要注意的就是，Y是一批的随机向量，y1，y2都是对应的一个token可以理解成每一个y就是一个句子，那么P（Y）代表的就是这些随机向量的分布。
E：代表边，概率的依赖关系。
理解G（V，E）：首先概率图模型也是模型，类比线性回归模型，y=w*x+b进行建模，而概率图模型是通过G（V，E）进行建模的，又因为我们的概率图模型是由概率和图构成的，因此，概率和边都是变量就类似于线性回归中的w，b一样，因此我们通过，G（V，E）进行概率图模型的建模。
有向图（HMM）和无向图（CRF）：
贝叶斯网络（信念网络）都是有向的，马尔科夫网络无向。所以，贝叶斯网络适合为有单向依赖的数据建模，马尔科夫网络适合实体之间互相依赖的建模。具体地，他们的核心差异表现在如何求 
，即怎么表示
这个的联合概率。
1.有向图：
对于有向图，这么求联合概率：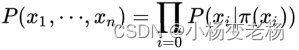
比如说下列这个有向图，我们想要对其建模：
应该这样表示他们的联合概率:
- 无向图：
对于无向图一般情况下指的就是马尔可夫网络。
在无向图中进行建模，需要将一个图分解成若干个团，而这些团必须是最大团，则有：
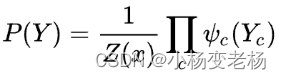
其中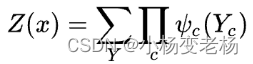
，这个很好理解，z就是一个归一化的因子，作用就是归一化，为了让结果是概率的形式。
所以说上边的无向图进行建模就变成了：
其中， 
是一个最大团
上随机变量们的联合概率，一般取指数函数的：
好了，管这个东西叫做势函数。
那么概率无向图的联合概率分布可以在因子分解下表示为：
这个也是CRF的开端。
齐次马尔可夫假设：
马尔可夫链是X（x1,x2,x3,x4......xn）这里边的xi只受xi-1的影响，也就相当于是一个2-gram。
生成式模型和判别式模型：
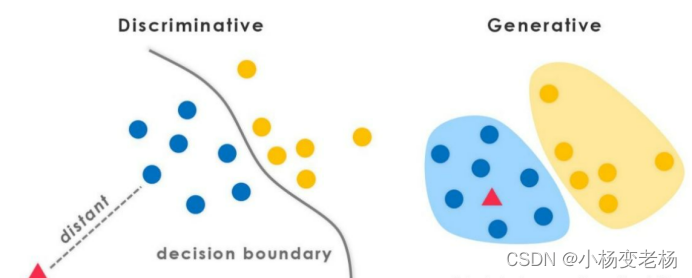
其实机器学习的任务是从属性X预测标记Y，即求概率P(Y|X)；
对于判别式模型来说求得P(Y|X)，对没有见过的待测样本X，根据P(Y|X)可以求得标记Y，即可以直接判别出来，如上图的左边所示，实际是就是直接得到了判别边界，所以传统的机器学习算法如逻辑回归模型、支持向量机SVM等都是判别式模型，这些模型的特点都是输入属性X可以直接得到Y（对于二分类任务来说，实际得到一个score，当score大于阈值时则为正类，否则为反类）
那么判别式模型。判别模型的特征，所以有句话说：判别模型是直接对 
建模，就是说，直接根据X特征来对Y建模训练。
具体地，我的训练过程是确定构建 
模型里面“复杂映射关系”中的参数，完了再去inference一批新的sample。
所以判别式模型的特征总结如下：
- 对
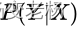建模 - 对所有的样本只构建一个模型，确认总体判别边界
- 观测到输入什么特征，就预测最可能的label
- 另外，判别式的优点是：对数据量要求没生成式的严格，速度也会快，小数据量下准确率也会好些。
而生成式模型求得P(Y,X)，对于没有见过的X，你要求出X与不同标记之间的联合概率分布，然后大的获胜，如上图右边所示，并没有什么边界存在，对于未见示例（红三角），求两个联合概率分布（有两个类），比较一下，取那个大的。机器学习中朴素贝叶斯模型、隐马尔可夫模型HMM等都是生成式模型，拿朴素贝叶斯举例，对于输入X，需要求出好几个联合概率，然后较大的那个就是预测结果。
同样，生成式模型。并且需要注意的是，在模型训练中，我学习到的是X与Y的联合模型 
，也就是说，我在训练阶段是只对
建模，我需要确定维护这个联合概率分布的所有的信息参数。完了之后在inference再对新的sample计算
，导出 , 但这已经不属于建模阶段了。
结合贝叶斯过一遍生成式模型的工作流程。学习阶段，建模： 
, 然后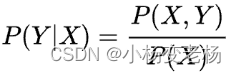 
。
另外，LDA也是这样，只是他需要确定很多个概率分布，而且建模抽样都蛮复杂的。
所以生成式总结下有如下特点：
- 对
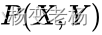建模 - 这里我们主要讲分类问题，所以是要对每个label（yi）都需要建模，最终选择最优概率的label为结果，所以没有什么判别边界。
- 生成式模型的优点在于，所包含的信息非常齐全，称之为“上帝信息”，所以不仅可以用来输入label，还可以干其他的事情。生成式模型关注结果是如何产生的。但是生成式模型需要非常充足的数据量以保证采样到了数据本来的面目，所以速度相比之下，慢。
举一个例子：
判别式模型举例：要确定一个羊是山羊还是绵羊，用判别模型的方法是从历史数据中学习到模型，然后通过提取这只羊的特征来预测出这只羊是山羊的概率，是绵羊的概率。
生成式模型举例：利用生成模型是根据山羊的特征首先学习出一个山羊的模型，然后根据绵羊的特征学习出一个绵羊的模型，然后从这只羊中提取特征，放到山羊模型中看概率是多少，在放到绵羊模型中看概率是多少，哪个大就是哪个。
二者目的都是在使后验概率最大化，判别式是直接对后验概率建模，但是生成模型通过贝叶斯定理这一“桥梁”使问题转化为求联合概率。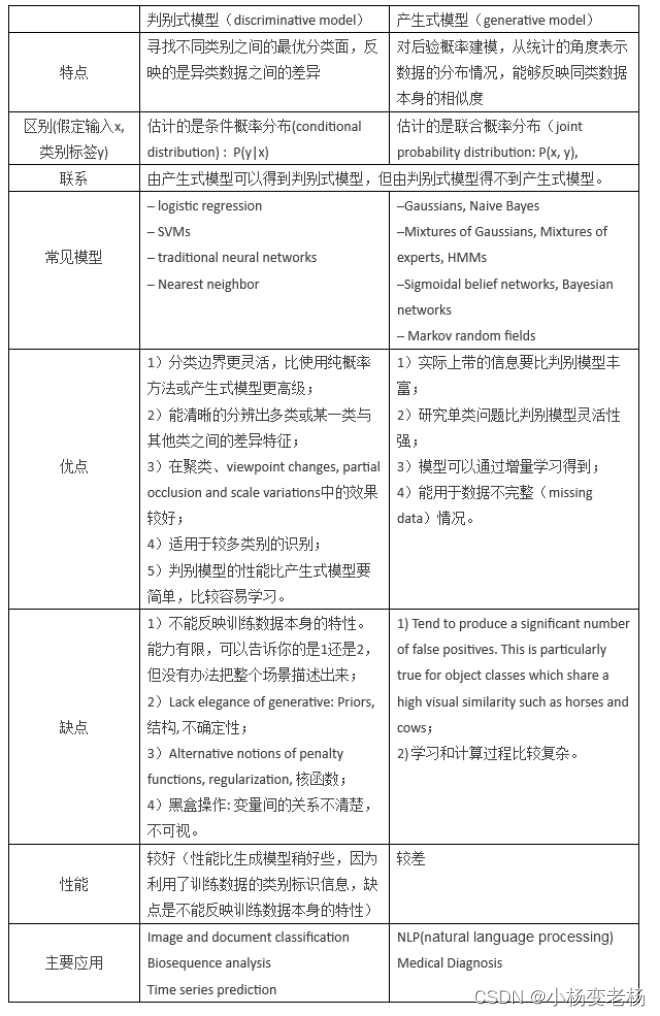
序列标注是一类特殊的分类任务，分类问题就不用细说了，标注问题相当于是分类问题的一个拓展，分类是输入一个序列得到一个分类结果，而标注问题，输入的是一个序列，输出的也是一个序列，标注问题输出的是一个向量，分类问题输出的是一个标签。
区分一下深度学习的标注和机器学习的标注。
