文章阅读

文章阅读
二分搜索代码框架常应用于「在有序数组中搜索指定元素」这个基本场景，具体的实际问题可以没有那么直接，但是也可以使用二分搜索进行解决
实际问题一般都让你求最值，比如让你求吃香蕉的「最小速度」，让你求轮船的「最低运载能力」，求最值的过程，必然是搜索一个边界的过程

套路

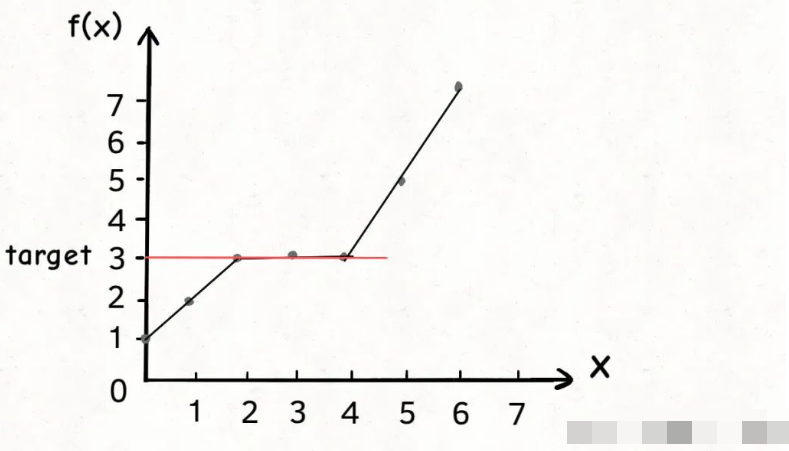
首先，你要从题目中抽象出一个自变量x，一个关于 x 的函数f（x），以及一个目标值target。
同时，x，f（x），target 还要满足以下条件:
1、f（x）必须是在x上的单调函数（单调增单调减都可以，大部分是递减的）
2、题目是让你计算满足约束条件f（x）== target 时的 x 的值。
然后通过搜素左边界或者右边界完成，不懂的去专栏学一下
在这里插入图片描述

题目

1011. 在 D 天内送达包裹的能力

class Solution {
    public int shipWithinDays(int[] weights, int days) {
        int max = 0, sum = 0;
        for(int w : weights){
            max = Math.max(max, w);
            sum += w;
        }
        int left = max, right = sum;
        while(left <= right){
            int mid = (left + right) >> 1;
            if(f(weights, mid) <= days){//单调递减的
                right = mid - 1;
            }else{
                left = mid + 1;
            }
        }
        return left;
    }
    //运载能力为x的时候，需要的f(x)天数，单调递减的
    public int f(int[] weights, int x){
        int days = 0;
        int i = 0;
        while(i < weights.length){
            int cap = x;
            while(i < weights.length){
                if(cap < weights[i]) break;
                else cap -= weights[i];
                i++;
            }
            days++;
        }
        return days;
    }
}

410. 分割数组的最大值

class Solution {
    public int splitArray(int[] nums, int k) {
        int max = 0, sum = 0;
        for(int w : nums){
            max = Math.max(max, w);
            sum += w;
        }
        int left = max, right = sum;
        while(left <= right){
            int mid = (left + right) >> 1;
            if(f(nums, mid) <= k){//单调递减的
                right = mid - 1;
            }else{
                left = mid + 1;
            }
        }
        return left;
    }
    //子数组各自和的最大值为x的时候，需要的f(x)连续子数组个数，单调递减的
    public int f(int[] weights, int x){
        int res = 0;
        int i = 0;
        while(i < weights.length){
            int sum = x;
            while(i < weights.length){
                if(sum < weights[i]) break;
                else sum -= weights[i];
                i++;
            }
            res++;
        }
        return res;
    }
}

875. 爱吃香蕉的珂珂

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int left = 1, right = 0;
        if(h == 1000000000) return 3;
        for(int p : piles) right = Math.max(right, p);
        while(left <= right){
            int mid = (left + right) >> 1;
            if(f(piles, mid) <= h) right = mid - 1;
            else left = mid + 1;
        }
        return left;
    }
    //吃香蕉的速度为x，则需要花费f(x)小时
    public int f(int[] piles, int x){
        int hour = 0;
        for(int p : piles){
            hour += p / x;
            if(p % x > 0){
                hour++;
            }
        }
        return hour;
    }
}