---

1、01背包理论基础

教程视频：https://www.bilibili.com/video/BV1cg411g7Y6

背包问题概述

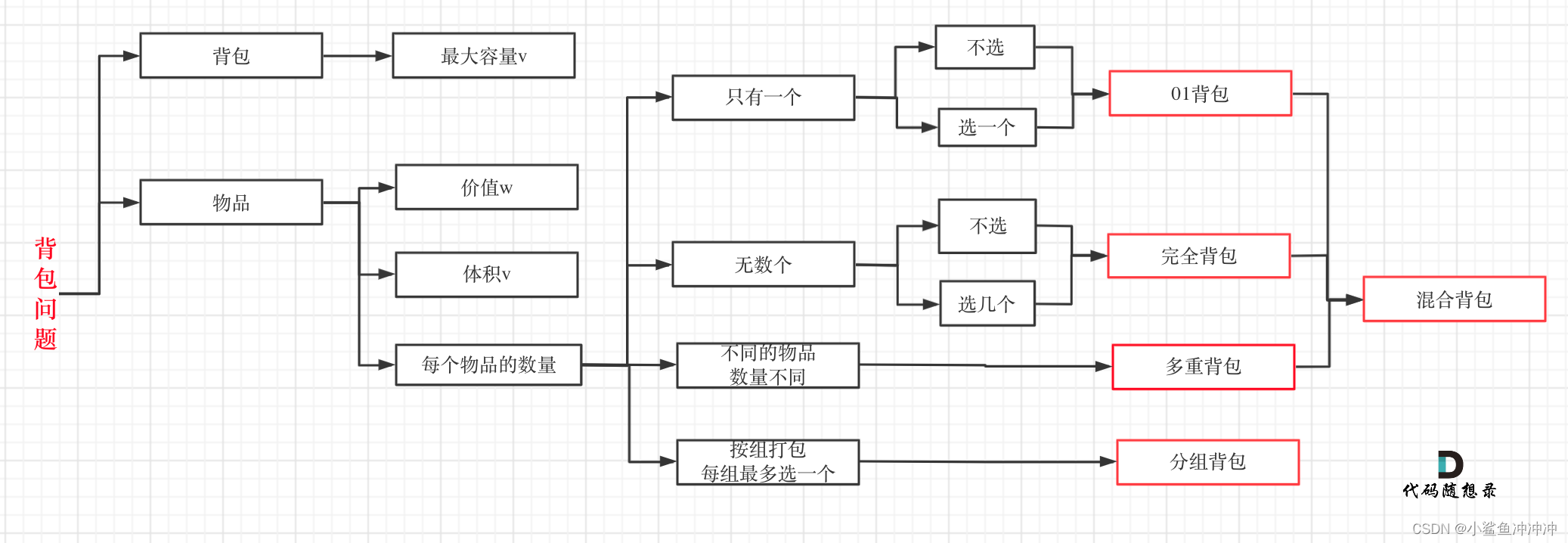重点掌握01 背包和完全背包即可。

01背包

问题：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

暴力解法：每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是$o(2^n)$，这里的n表示物品数量。

因为暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

二维dp数组01背包案例

背包最大重量为4。
物品为：

物品	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

动态规划分析：

1. 确定dp数组以及下标的含义
   这里使用二维数组解决。即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

	物品编号(i) \ 背包容量(j)	0	1	2	3	4
物品0	0	0	15	15	15	15
物品1	1	0	dp[1][1]	dp[1][2]	dp[1][3]	dp[1][4]
物品2	2	0	dp[2][1]	dp[2][2]	dp[2][3]	dp[2][4]

2. 确定递推公式
   有两个方向推出来dp[i][j]：
   不放物品i ：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)在表格中表现为正上方格子值+当前行的物品价值。
   放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值。

   因此dp[i][j]=Math.max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);

3. dp数组如何初始化
   背包容量为0时，最大价值为0，即dp[*][0]=0;
   对第一件物品来说，背包容量不够时最大价值为0；从能放进背包那一刻开始，背包的最大价值等于value[0]。
   剩余位置初始为什么数值都可以，因为都会被覆盖。

4. 确定遍历顺序
   双层for循环，一层遍历物品，一层遍历背包。
   在本题中，只要保持dp[<i][<=j]处都有值即可，因此两层循环顺序调换并不影响最终结果。

5. 举例推导dp数组
   做动态规划的题目，最好的过程就是自己在纸上举一个例子把对应的dp数组的数值推导一下，然后再动手写代码！

class Solution{
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testBagProblem(weight,value,bagSize);
    }

	public static void testBagProblem(int[] weight, int[] value, int bagSize){
		// 创建dp数组
		int[][] dp = new int[weight.length][bagSize+1];
		// 初始化dp数组
		for(int i=0;i<weight.length;i++){
			dp[i][0]=0;
		}
		for(int i=0;i<=bagSize;i++){
			if(i>=weight[0]){
				dp[0][i]=value[0];
			}
			dp[0][i]=0;
		}
		// 填充dp数组
		for(int i=1;i<weight.length;i++){
			for(int j=1;j<=bagSize;j++){
			if(j>=weight[i]){
				//当前背包的容量大于等于当前物品i的时候，比较两种情况下，哪种最大价值最大
				dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
			}else{
				dp[i][j] = dp[i-1][j];
			}
			}
		}
		//打印
		for (int i = 0; i < weight.length; i++) {
            for (int j = 0; j <= bagSize; j++) {
                System.out.print(dp[i][j] + "\t");
            }
            System.out.println("\n");
        }
	}
}

2、01背包理论基础（滚动数组）

教程视频：https://www.bilibili.com/video/BV1BU4y177kY
滚动数组，其实就是将二维dp表格解决降为一维dp数组，一些录友当时还表示比较困惑。

1. 确定dp数组的定义
   在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。
2. 一维dp数组的递推公式
   dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
3. 一维dp数组如何初始化
   下标0的位置，即dp[0]初始为0。
   从递归公式可以看出，dp数组在推导的时候一定是取价值最大的数，所以如果题目给的价值都是正整数，那么非0下标都初始化为0就可以了。
4. 一维dp数组遍历顺序
   此时因为将对于物品的遍历压缩到一位数组中，需要先遍历物品，再遍历背包容量。
   为了利用上次循环的状态，同时保证物品i只被放入一次，背包容量需要倒序遍历。
5. 举例推导dp数组

class Solution{
    public static void main(String[] args) {
        int[] weight = {1,3,4};
        int[] value = {15,20,30};
        int bagSize = 4;
        testBagProblem(weight,value,bagSize);
    }
    public static void testBagProblem(int[] weight, int[] value,int bagSize){
    	//定义dp数组
    	int[] dp = new int[bagSize+1];
    	//dp数组初始化（默认全为0，可以不显示初始化）
    	for(int i=0;i<weight.length;i++){
    		
    		for(int j=bagSize;j>=0;j--){
	    		if(j>weight[i]){
	    			dp[j] = Math.max(dp[j], dp[j-weight[i]]+value[i]);
	    		}//这里可以化简，还可以把if判断放在for循环条件中
	    		//else{
	    			//dp[j]=dp[j];
	    		//}
    		}
    		//打印dp数组
	        for (int j = 0; j <= bagSize; j++){
	            System.out.print(dp[j] + " ");
	        }
    	}
    }
}

---

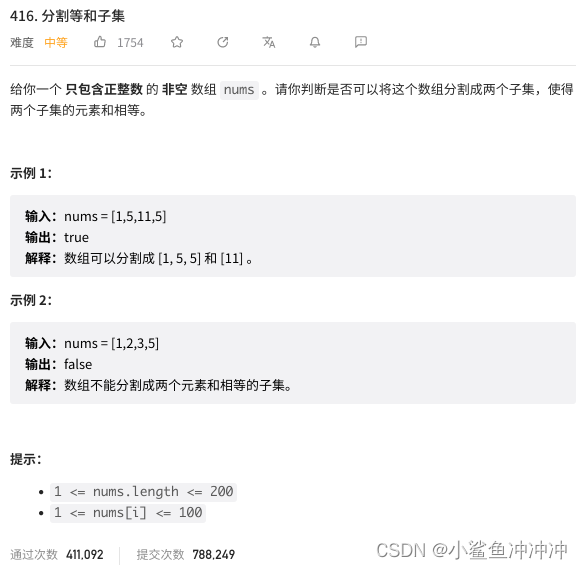
3、 416. 分割等和子集

教程视频：https://www.bilibili.com/video/BV1rt4y1N7jE

解法一：动态规划

注意题目描述中商品是不是可以重复放入。所以本题中，要使用的是01背包，因为元素只能用一次。

只有确定了如下四点，才能把01背包问题套到本题上来：
1、背包的体积为sum / 2
2、背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
3、背包如果正好装满，说明找到了总和为 sum / 2 的子集。
4、背包中每一个元素是不可重复放入。

1. 确定dp数组以及下标的含义
   dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。
2. 确定递推公式（物品i的重量是nums[i]，其价值也是nums[i]）
   dp[j]=Math.max(dp[j], dp[j-nums[i]]+nums[i]);
3. dp数组如何初始化
   首先dp[0]是0。
   题目给的价值都是正整数，所以非0下标都初始化为0。
4. 确定遍历顺序
   同理滚动数组，外层for循环遍历nums中数值，内层for循环反向遍历背包容量。
5. 举例推导dp数组
   dp[j]的数值一定是小于等于j的。
   如果dp[j] == sum/2，即背包正好装满，说明集合中的子集总和正好可以凑成sum/2。

class Solution {
    public boolean canPartition(int[] nums) {
        int sum=0;
        for(int i=0;i<nums.length;i++){
            sum+=nums[i];
        }
        //总和为奇数，不能平分
        if(sum%2==1){return false;}

        int[] dp = new int[sum/2+1];
        for(int i=0;i<nums.length;i++){
            for(int j=sum/2;j>=nums[i];j--){
                //物品 i 的重量是 nums[i]，其价值也是 nums[i]
                dp[j]=Math.max(dp[j], dp[j-nums[i]]+nums[i]);
            }
        }
        return dp[sum/2] == sum/2;
    }
}

---