网上有很多关于多维空间的描述,这里分享一下我的个人理解
假设在二维空间中有两个图形,三角形、四边形,画面如下

以如下规律在三维空间展开
- 对于三角形,在三维空间中添加一点,和其连接,使得每个面都为三角形
- 对于四边形,在三维空间中需要添加四点,并连接相应的点,使得每个面都为四边形。
那么新的形状在2维空间的投影就变成

按照同样的规律在四维空间展开
- 对于三角体,在第四维空间添加一个点,并和三维中所有点连接,使得每个六个边都能围成一个三角体
- 对于正方体,在第四维空间添加一个四方体,和三维中的八个点连接,使得每八个面都能围成一个正方体
那么新的形状在2维空间的投影就变成

高维形状在低维投影可变形,且依然符合形状特征
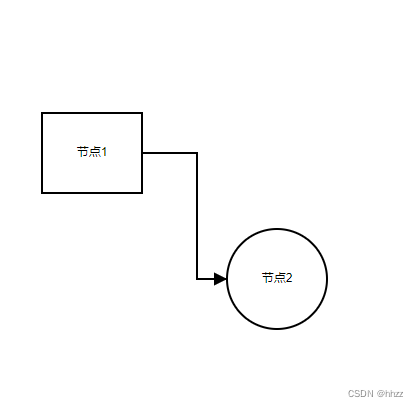
将上面的投影适当变形,就能看到网上说的超三角体、超正方体,但我觉得并没有意义,因为在更高的维度,这种形状难以想象,反倒是图3更适合扩展为多维图形

个人理解多维图形的意义
- 高维运算可以像【复数】一样用来解决低一维度的数学问题
- 【时间】不是四维,反而更像薛定谔、量子坍缩,存在于每一个维度,是一种不可逆的变化