下面来解释这些东西是怎么来的

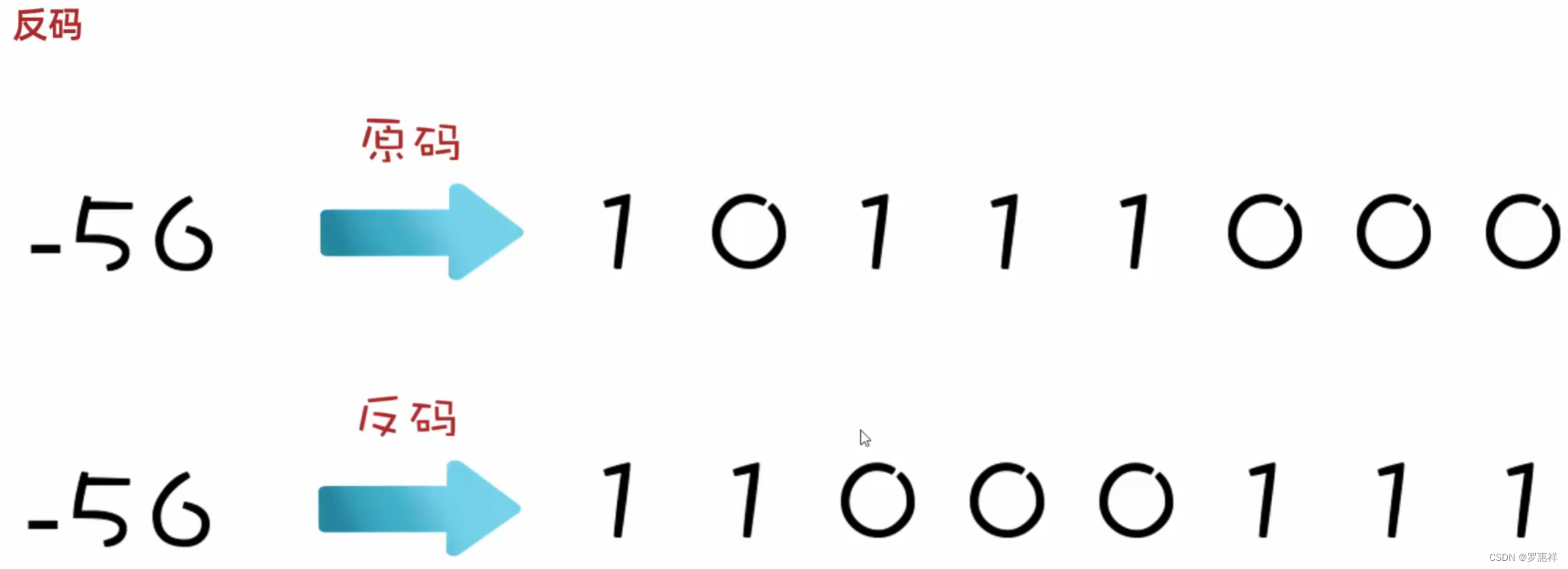
原码

例如： 

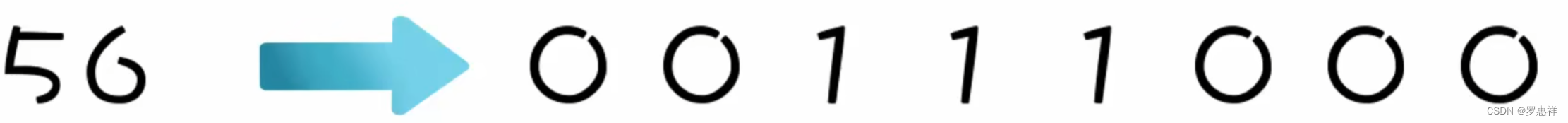
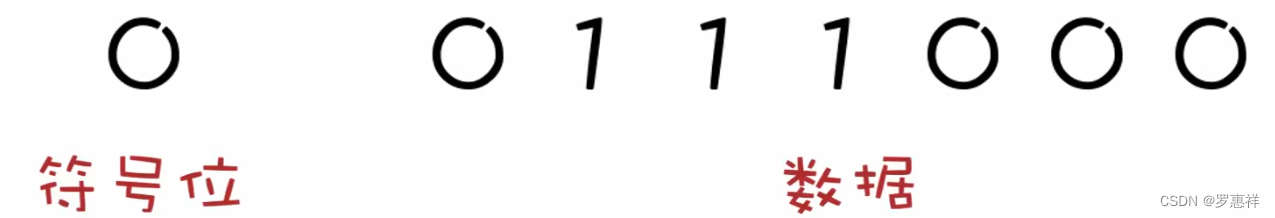
最左边的叫做符号位，0 为正，1 为负，后面的才是具体的数值

在计算机中，一个 0 或者 1 所占的空间叫 bit 中文名叫比特位，八个 bit 就称为一个字节，字节是计算机中最小的数据单位  

下面是一个字节可以表示的最大值和最小值（byte 类型占一个字节，但取值范围是 -128~127，到后面就会解释到一个字节表示的最大值和最小值其实是 -128~127）

原码的弊端

 1000_0000   表示  -0   在这个基础上我们进行 +1

 1000_0001   表示 -1    正确值：1，实际值：-1  在这个基础上我们在进行+1

 1000_0010   表示-2     正确值：0，实际值：-2  在这个基础上我们在进行+1

 1000_0011   表示-3     正确值：-1，实际值：-3 

从上面可以发现，在计算机运算的时候，因为没有正负号，只能采用 0，1 代表正负， 在进行

负数运算的时候会存在弊端 

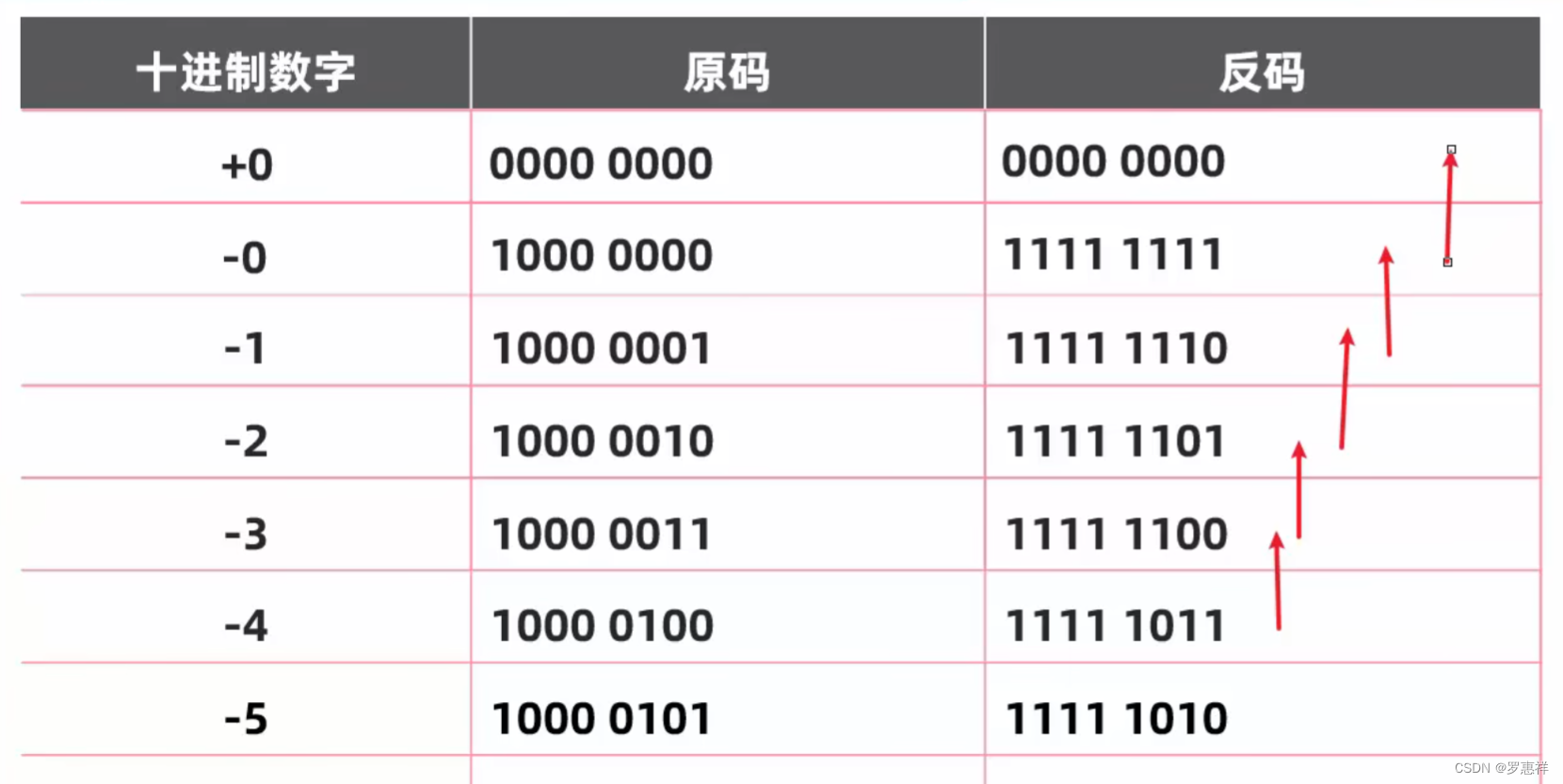
 反码

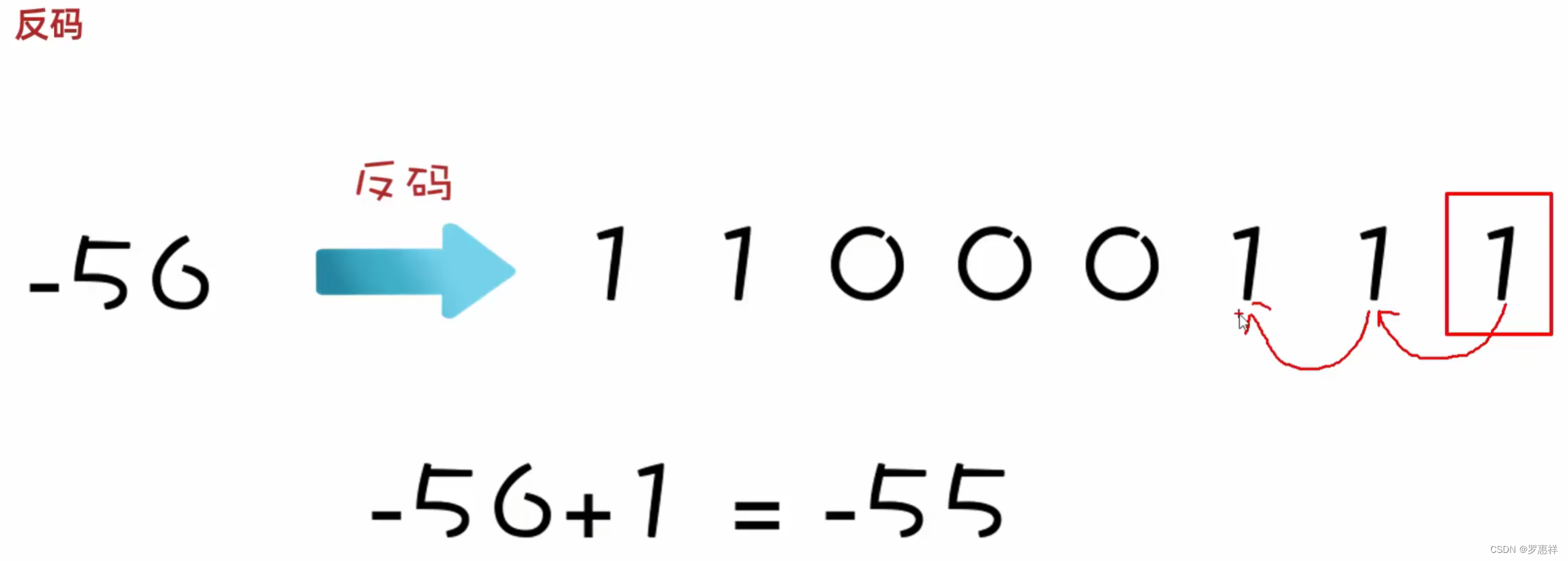
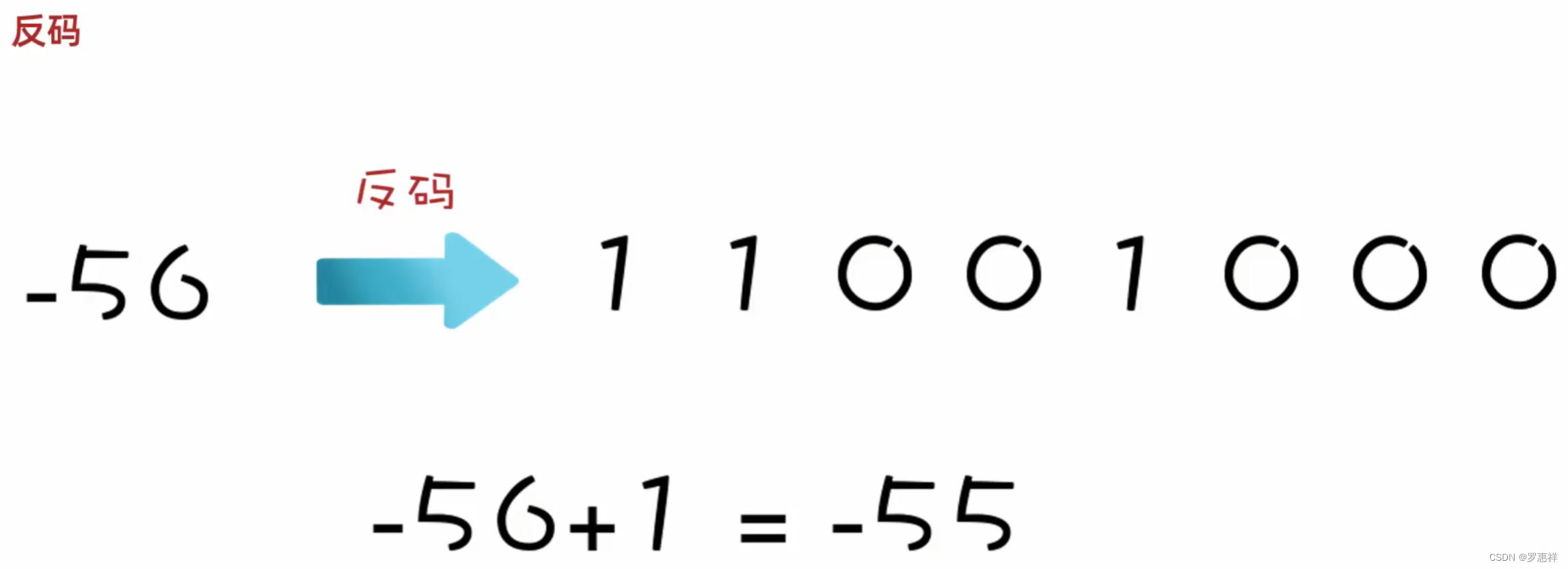
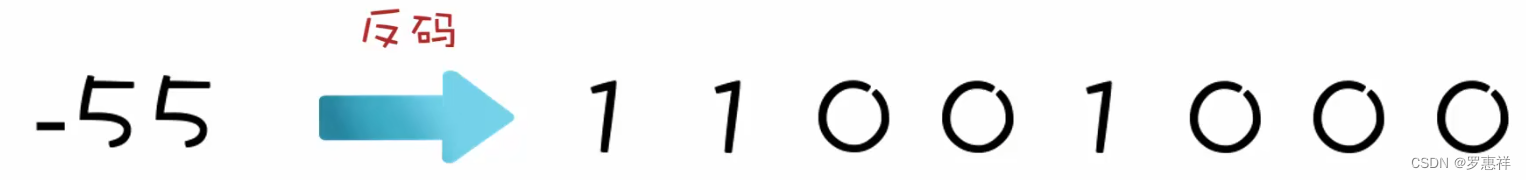
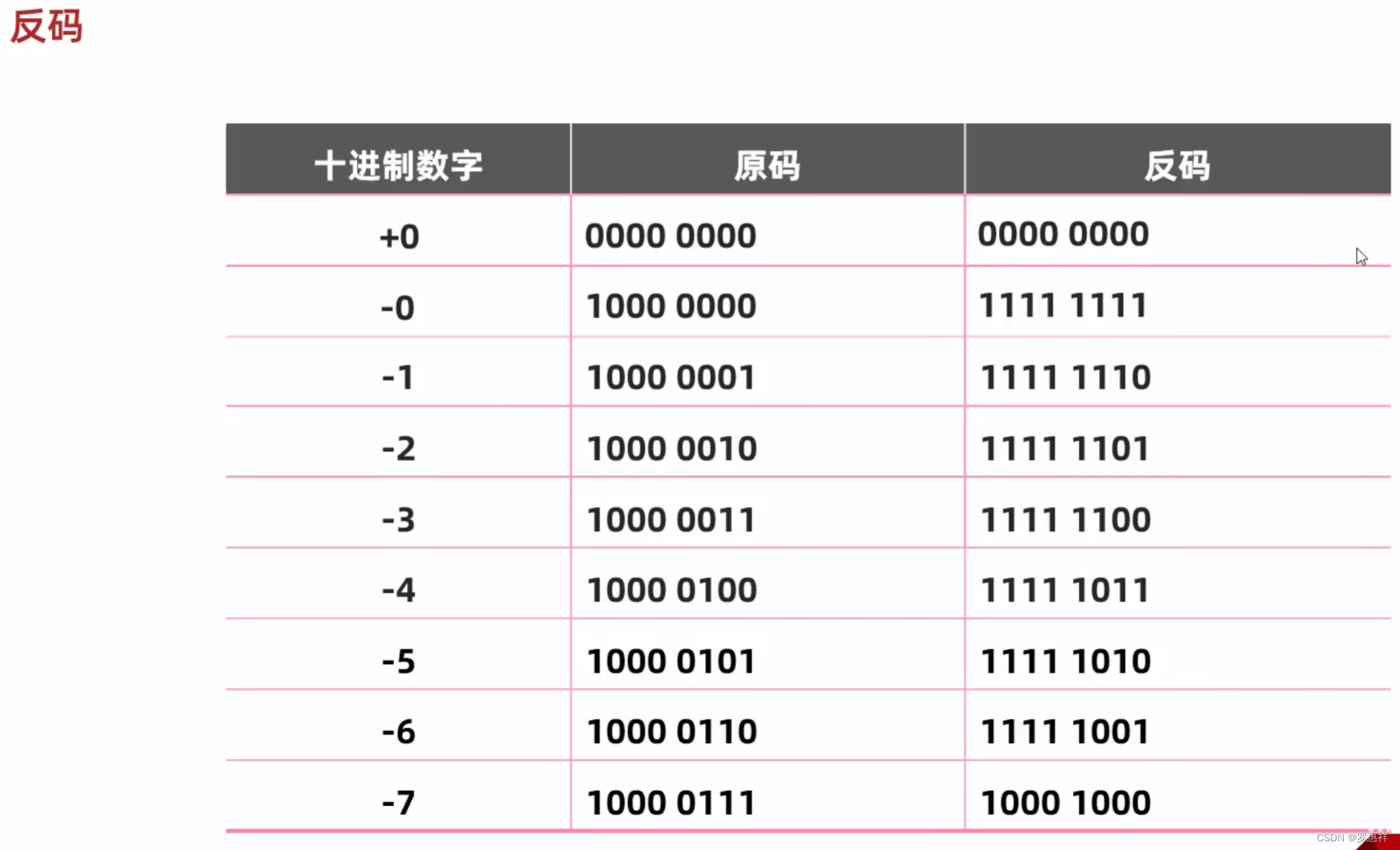
 我们可以发现，负数中反码运算的 +1 就是原码运算的 -1，取到了相反的作用， 从而解决了原码运算中负数的运算弊端

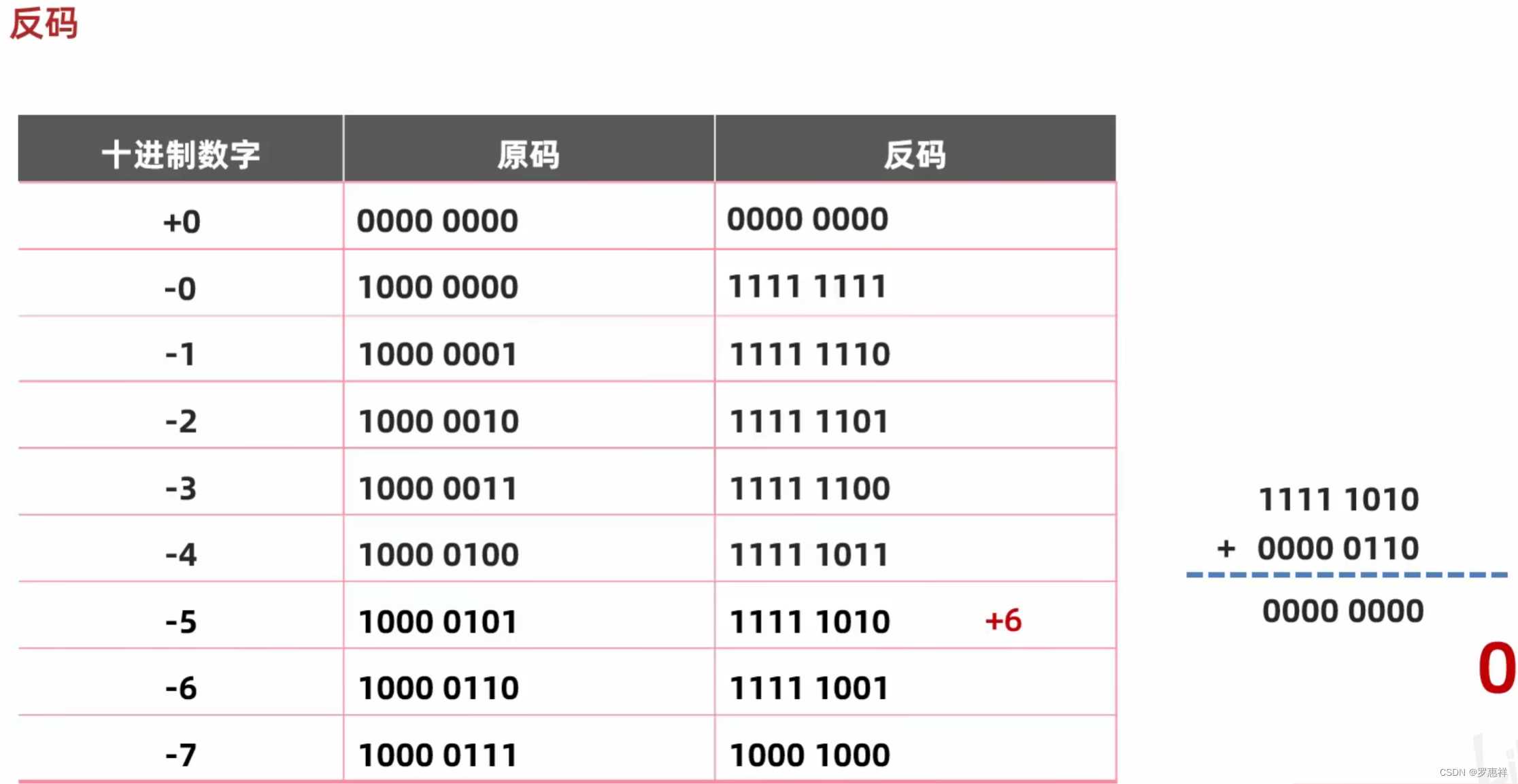
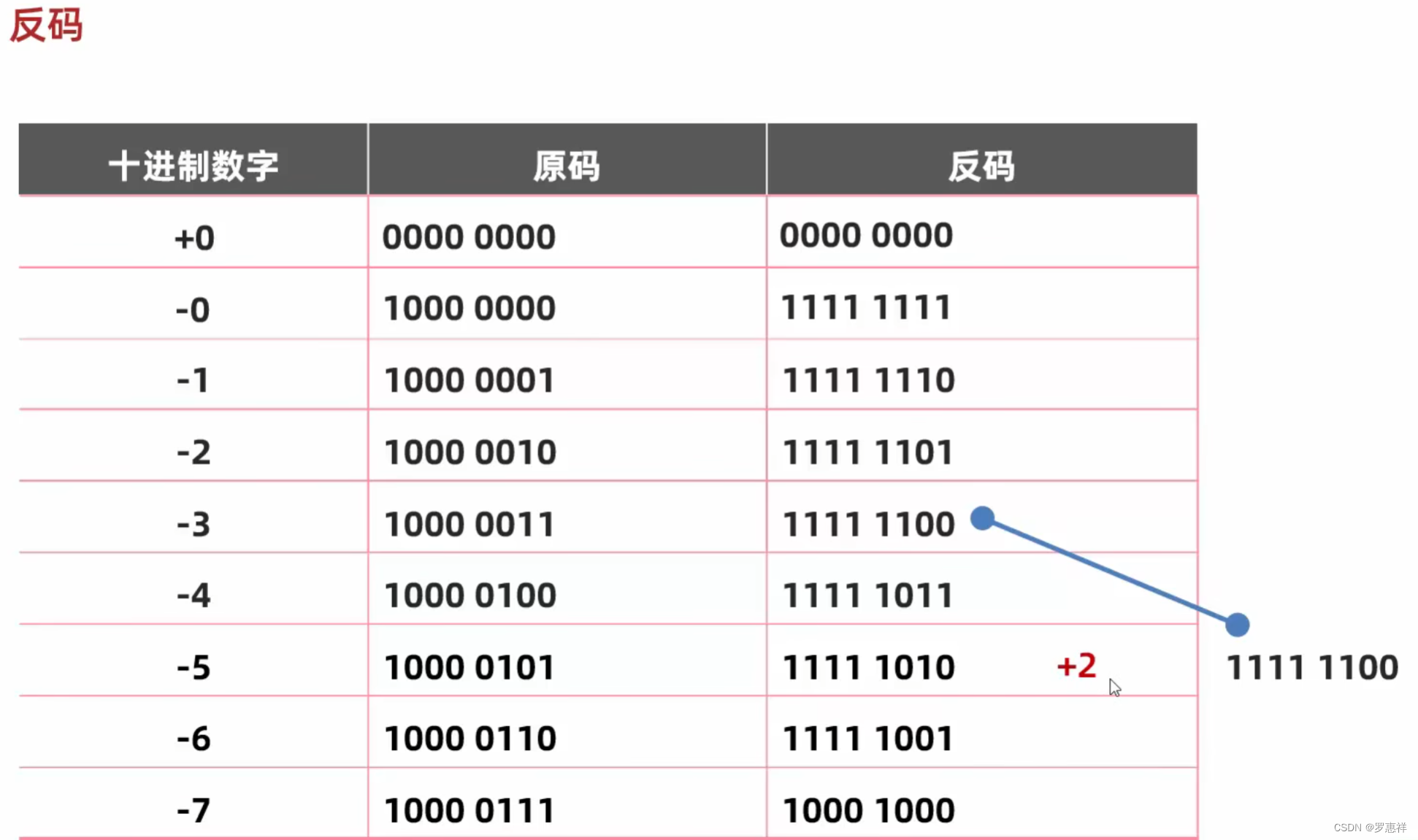
但同时又发现了一个问题，+0 和 -0 都是 0 但是反码和原码都不一样，所以当运用反码进行跨 0 运算的时候又产生了一个误差，例如：-5 + 6 的正确值为 1，但实际值却是 0  

补码

因为 0 又两个编码表示，为了减少一个 0 的编码，就出现了补码，

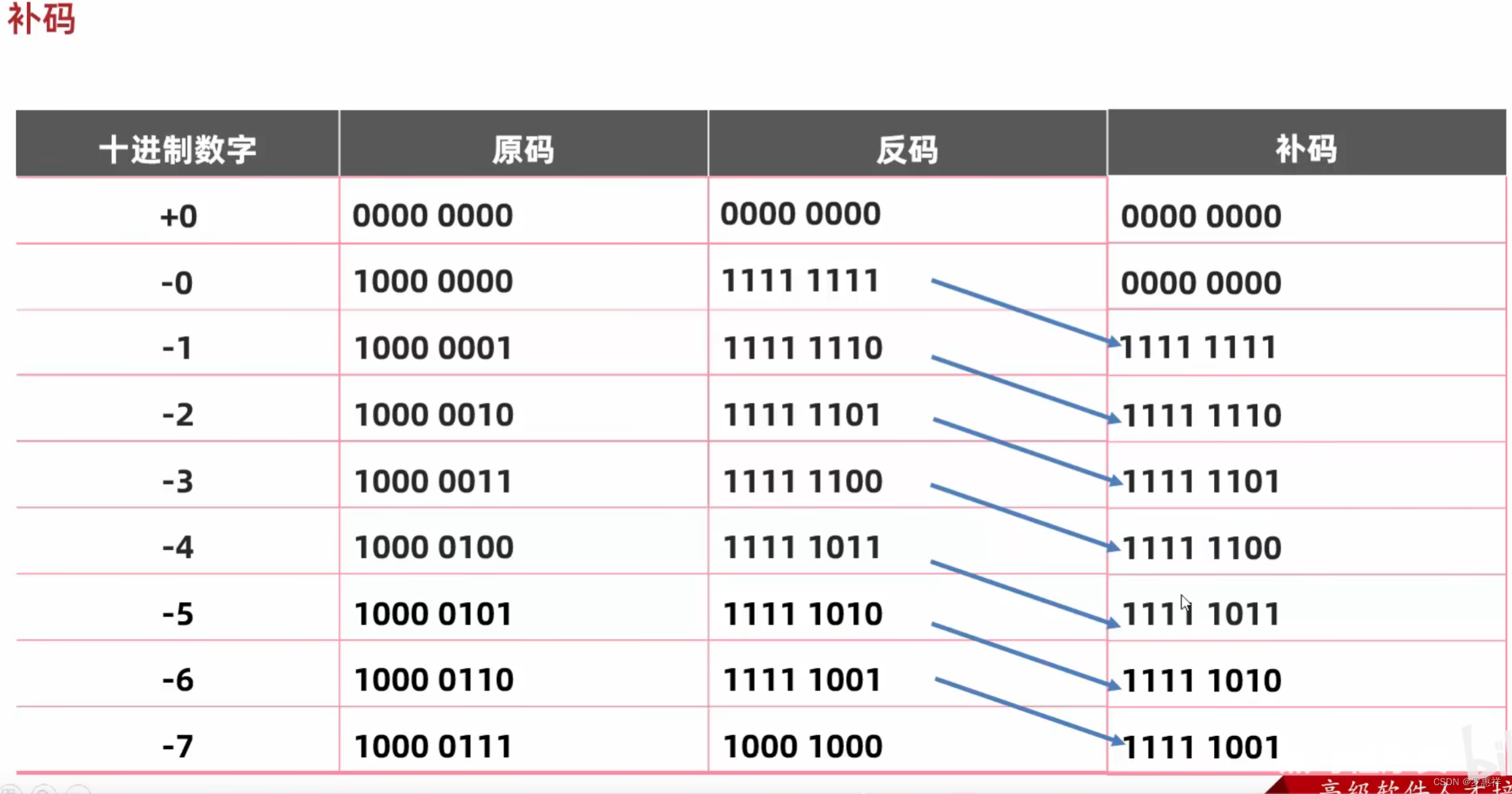
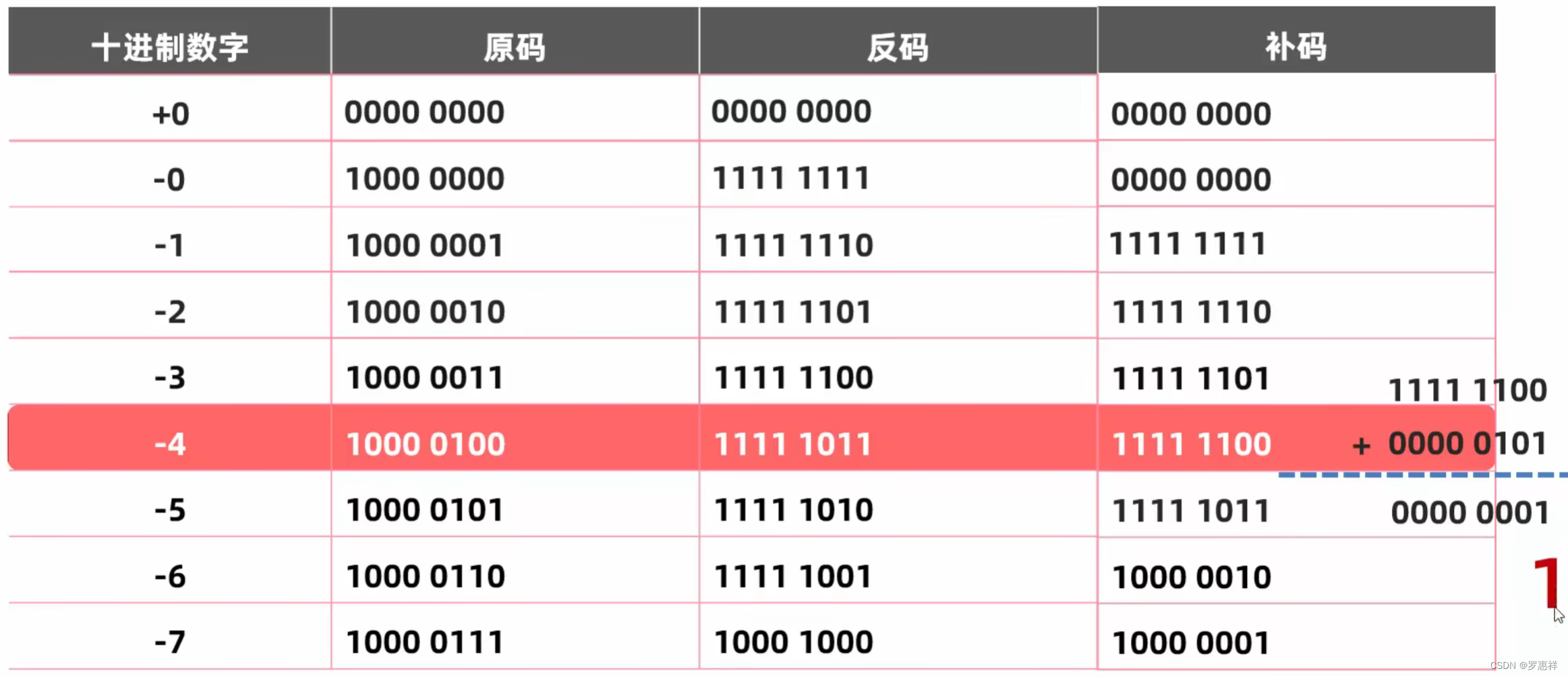
 补码就是将负数的反码在 +1 ，正数的依旧不变，这样讲反码错开一位之后，+0 和 -0 就是相同的表现形式，就避免了反码跨0运算误差的问题 

 也正是因为补码是错位的反码，所以  -127 的反码就给了 -128，这也就解释了为什么一个字节所表达的范围是  -128~127

也正是因为上面的原因，在计算机中数字的存储还有运算都是以补码的来进行运算的

小结

 在多学几招

 

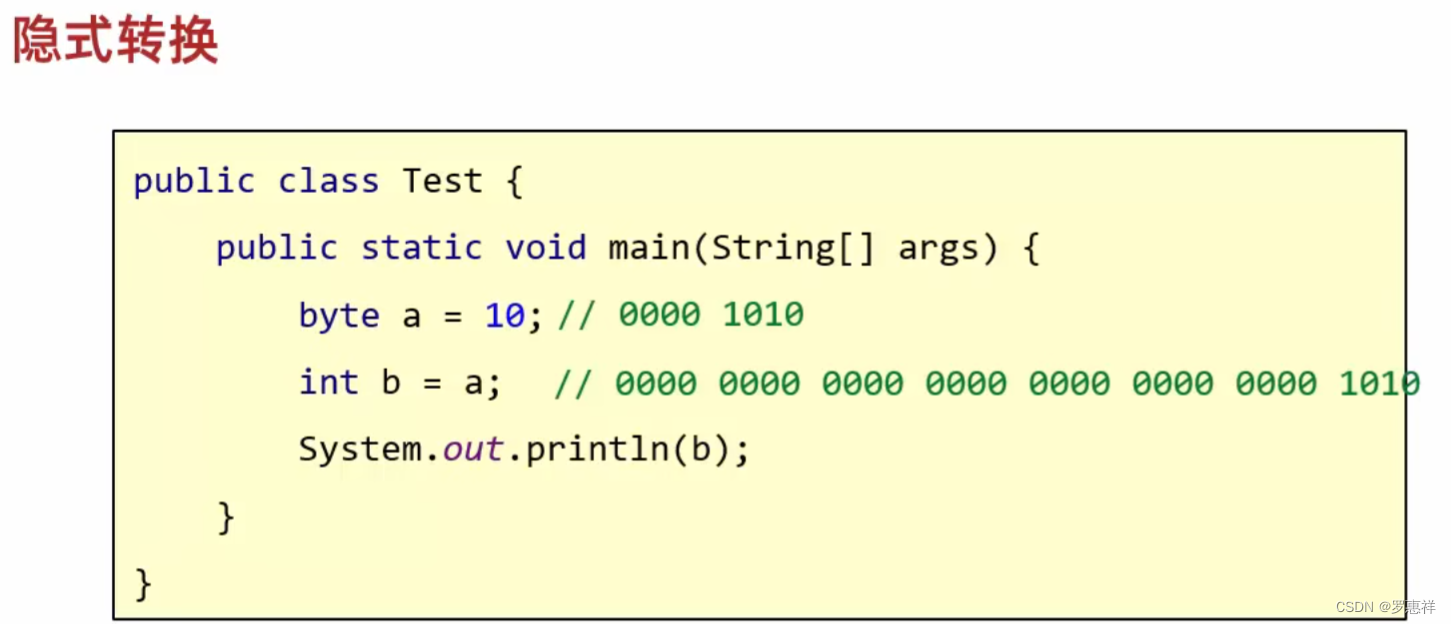
 隐形转换的底层就是前面进行补 0 即可

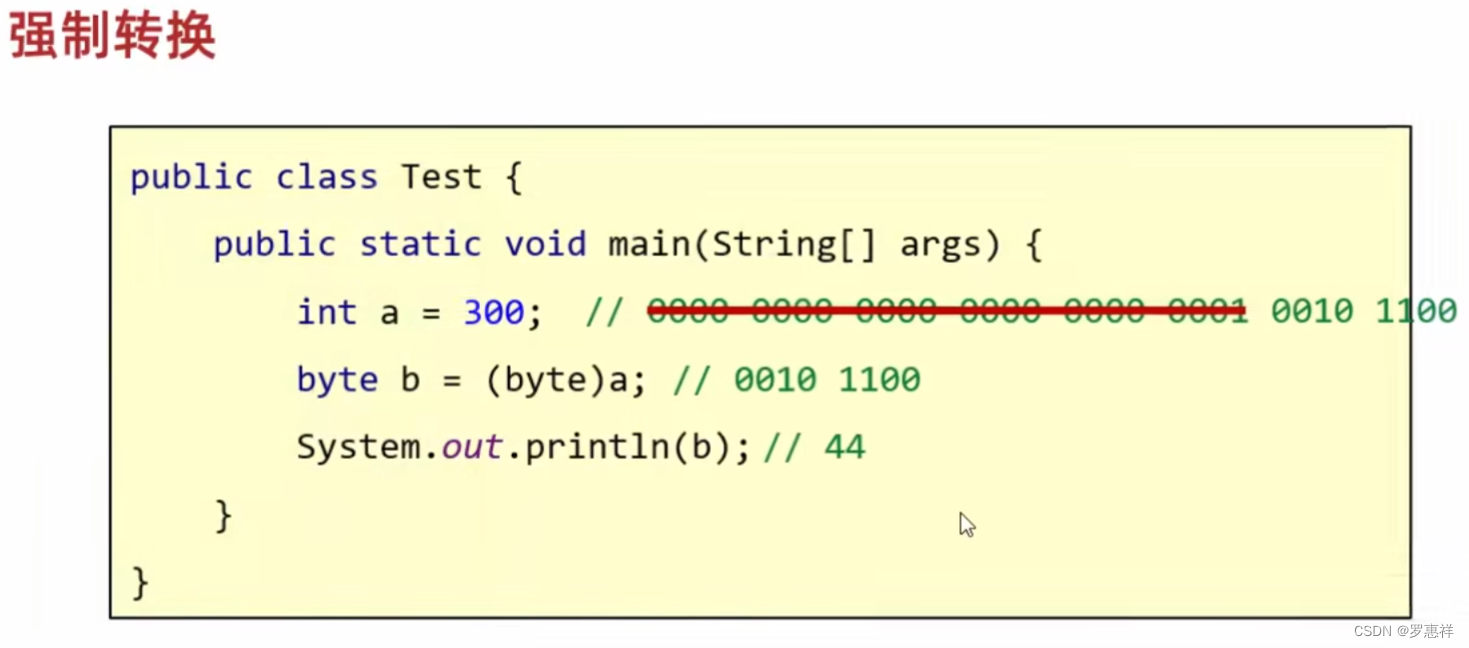
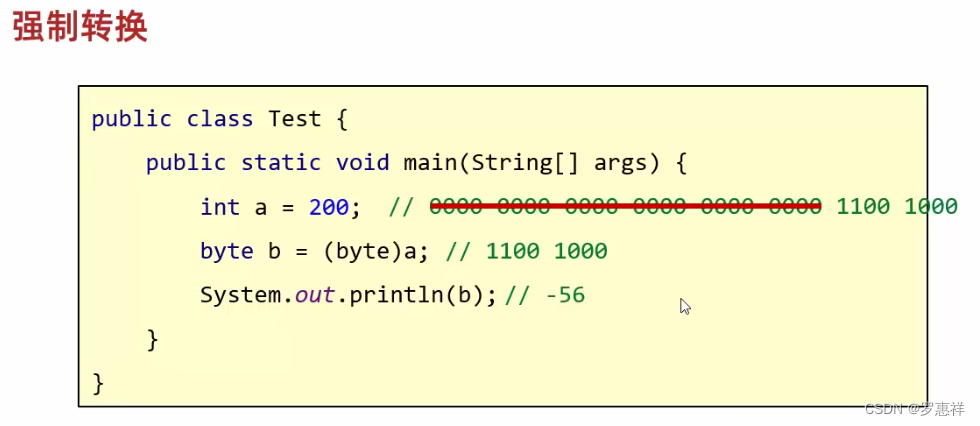
 强制转换的底层就是删掉前面多余的字节，所以在容量溢出和数值的正负上会有精度问题

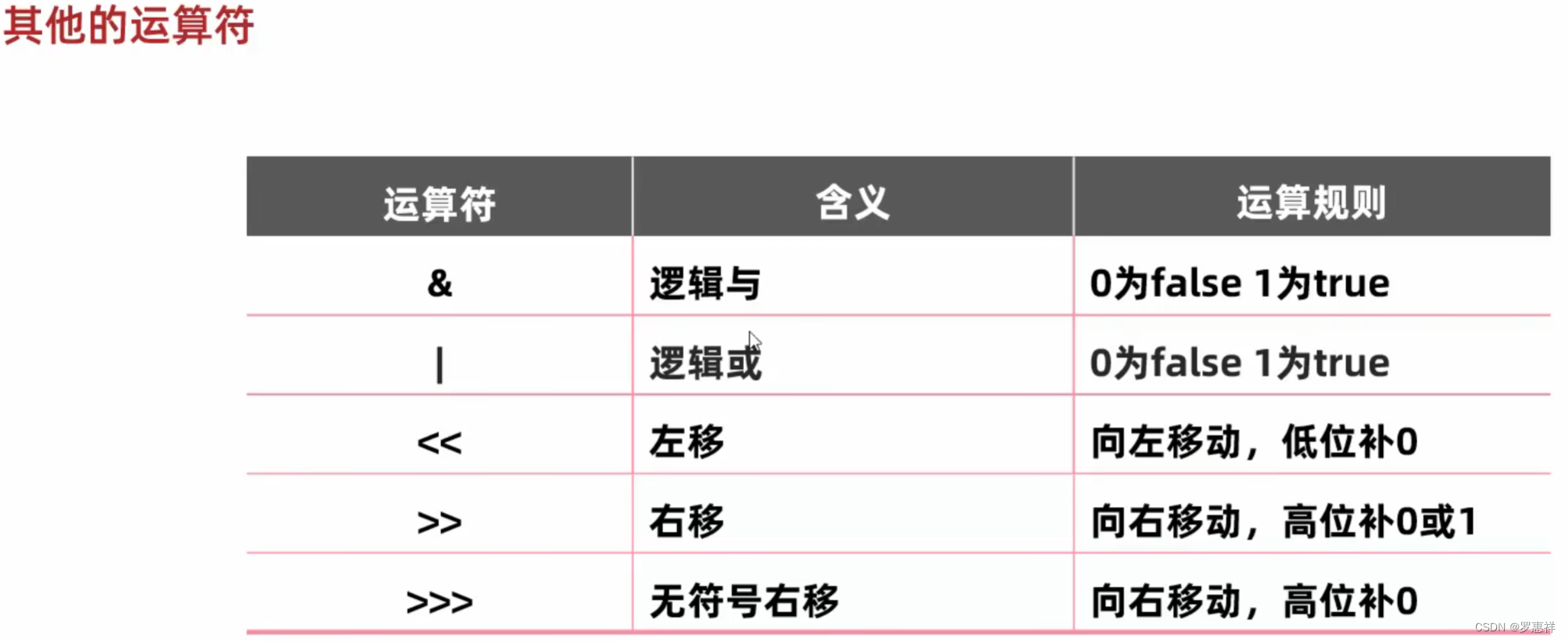
位运算符

 

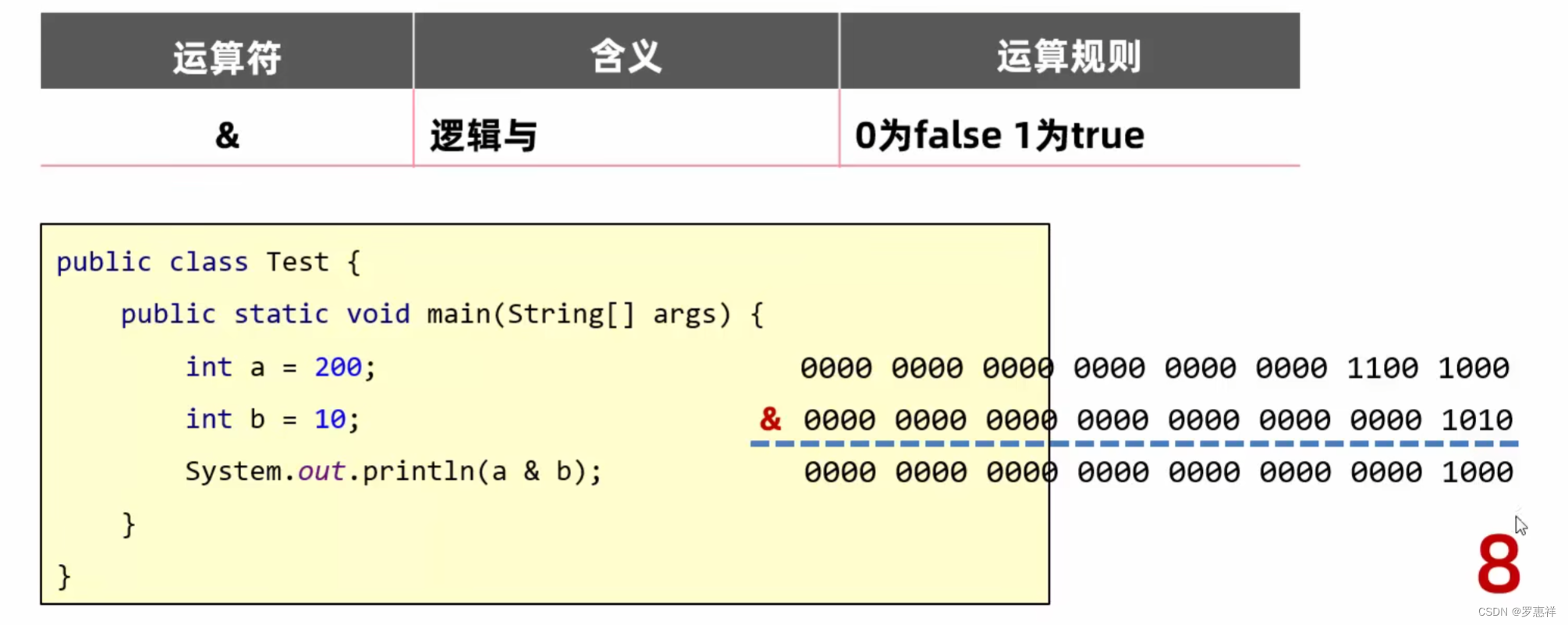
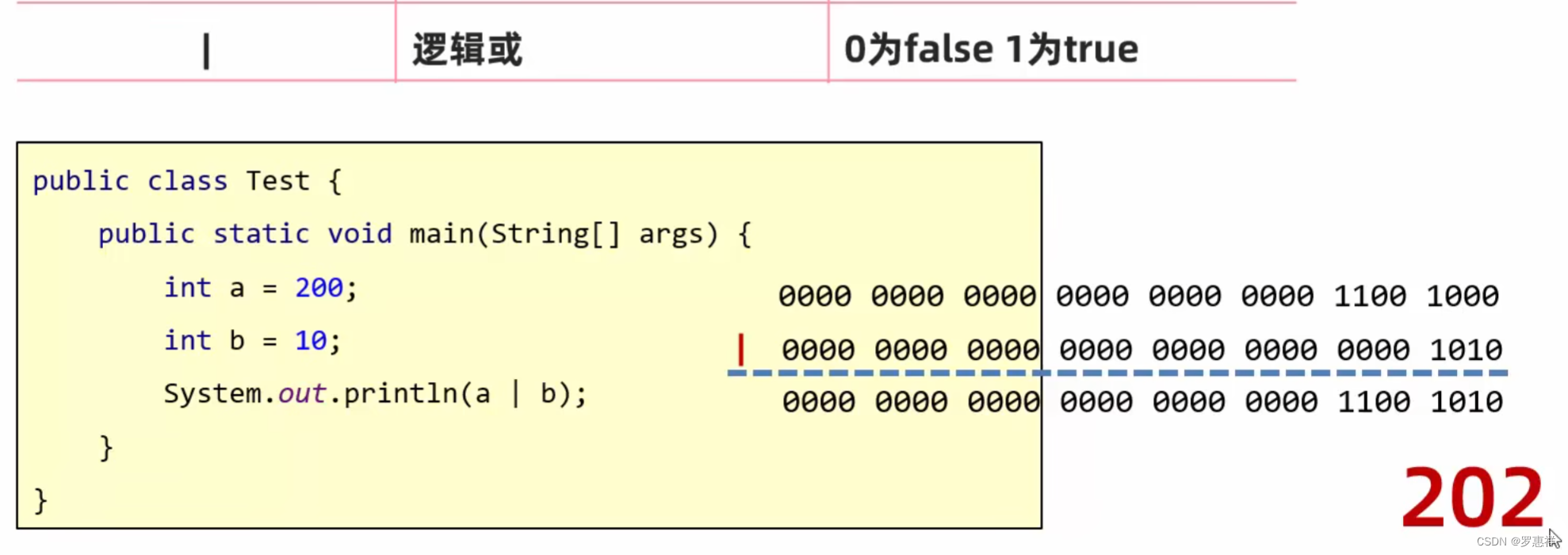
 左移一次就相当于 *2 

 补 0 和 1 根据原来的数值的正负来补对应的 0 和 1

右移一次就相当于 /2

 和右移类似，就是高位不管是正数还是负数都补 0

【黑马程序员Java零基础视频教程_上部(2022新版Java入门，含斯坦福大学练习题+力扣算法题+大厂java面试题）】https://www.bilibili.com/video/BV17F411T7Ao?p=38&vd_source=04c9e32408f61b4fd8bec53b61c24bd9