8.1 算法解释

分治问题 通过「把原问题分为子问题，再将子问题进行合并处理」，从而实现对原问题的求解。

归并排序就是典型的分治问题，“分”即为把大数组平均分成两个小数组，通过递归实现，得到很多个长度为 1 的子数组；“治”即为把已经排好序的两个小数组合并为一个排好序的大数组，从长度为 1 的子数组开始，最终合成一个大数组。

我们可以使用数学表达式来表示这个过程。定义 T(n) 表示处理一个长度为 n 的数组的时间复杂度，则归并排序的时间复杂度递推公式为：T(n) = 2T(n/2) + O(n) 。其中 2T(n/2) 表示我们分成了两个长度减半的子问题，O(n) 则为合并两个长度为 n/2 数组的时间复杂度。

那么如何利用递推公式得到最终的时间复杂度呢？可以使用主定理求解：

主定理
考虑T(n) = aT(n/b) + f(n)，定义 k=logb(a)

• 如果 f(n) = O(n^p) 且 p<k ，那么 T(n) = O(n^k)
• 如果存在 c>=0 且 f(n) = O(n^k log^c(n)) ，那么 T(n) = O(n^k log^(c+1)(n))
• 如果 f(n)=O(n^p) 且 p>k ，那么T(n) = O(f(n))

另外，自上而下的分治可以和 memorization 结合，避免重复遍历相同的子问题。如果方便推导，也可以换用自下而上的动态规划方法求解。

8.2 表达式问题

241. 为运算表达式设计优先级（中等）

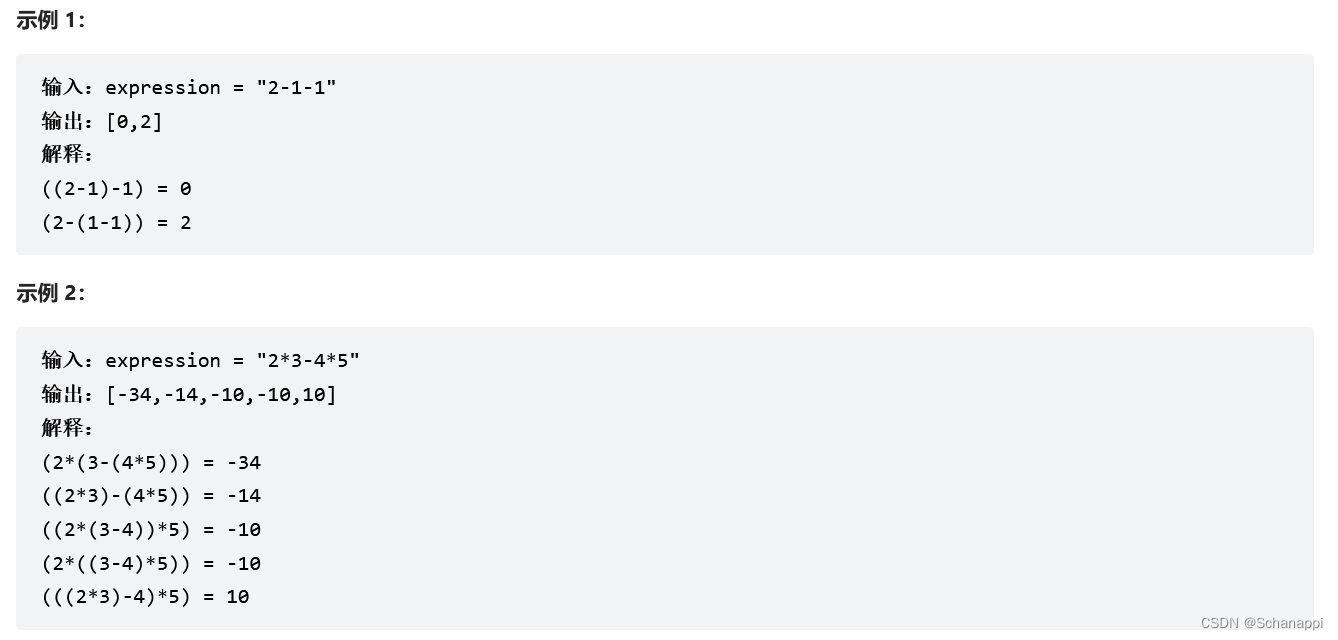
思路及代码： 241. 为运算表达式设计优先级

932. 漂亮数组（中等）

思路及代码： 932.漂亮数组

312. 戳气球（困难）

思路及代码： 312.戳气球