图和图搜索算法的基本概念

图的基础概念

图是有节点和边的一种表达方式

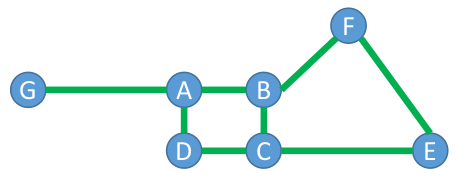
各节点由边连起来
边可以是有向的，也可以无向的

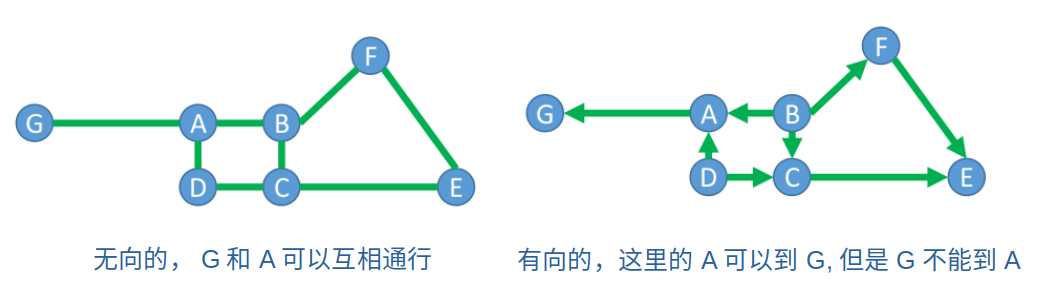
边也可以有权重，如果没有特殊说明，可以认为权重是一样的。
下面则是有权重的

在每条边上机器人付出的代价不一样，代价可能是路径或者更广义的概念，比如机器人消耗的能量，或者易出现的风险。

图搜索基本概念

对于任何一个图搜索算法，首先要构造一个图

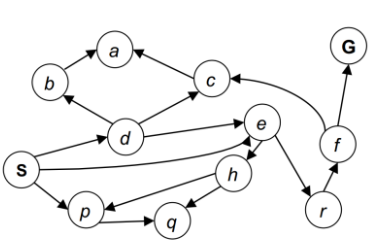
上图是抽象概念里的图

对于实际场景，我们需要人为构造一个图，以下是两种简单的例子

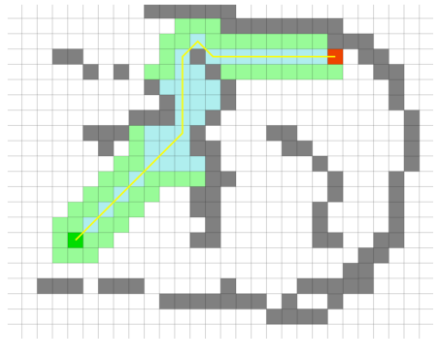
栅格地图的路径规划，里面的节点和相邻的节点是具有连接关系的，所以本身就是一个图了

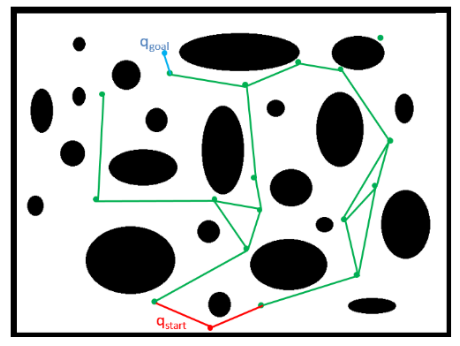
基于采样的，没有天然的节点关系，需要人为构造一个图在里面，例如上面就是通过算法构造的有节点和边组成的图

图搜索算法

搜索总是从起始状态Xs开始,到Xg结束
对于搜索节点，可以构建一个搜索树

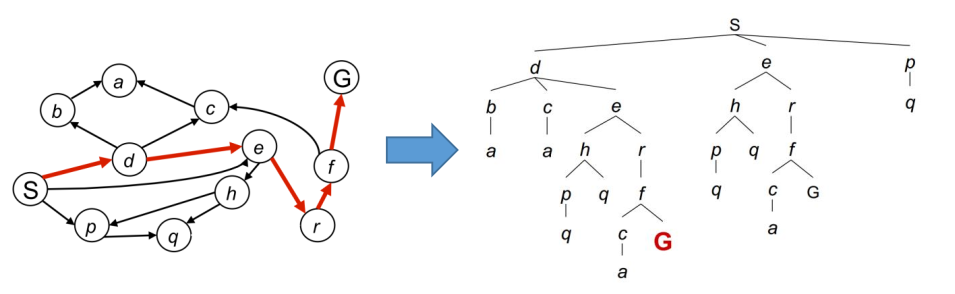
右边和左边是等价的，只是写成了树状的结构，这样看彼此关系更加清晰点

从起点搜索到终点后，回溯整个搜索过程，就可以得到希望的搜索路径

对于实际机器人来说，构建整个空间的搜索树，代价很大，所以需要尽可能快，但是不失搜索路径的算法。

图搜索算法框架

所有的图搜索算法都是按照下面的框架进行的:

1、维护一个容器，装载将来有可能访问的一个节点

2、容器初始化为空，放入的第一个节点就是起始状态Xs

3、循环：
根据预先定义的一个指标或者目的，从容器中弹出一个节点 ，称之为 访问一个节点
获取弹出节点所有的邻居节点， —扩展
将这些邻居节点装入容器

4、结束循环：访问到了结束状态，或者自定义的一个指标，结束循环

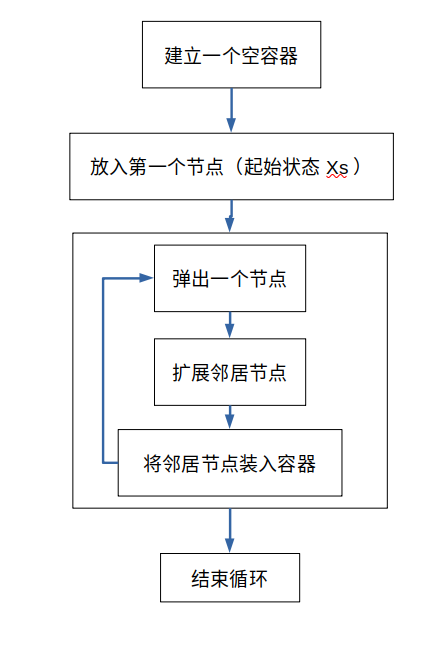
有两个下面的问题需要注意

什么时候结束循环？

• 一种可能就是容器空了，这代表没有了我们将来要访问的节点了，遍历完了所有节点
• 搜索到了结束节点

如果这个图本身是有回环的呢？
为了在图搜索中避免形成回环，永远走不出去，需要再维护一个新的容器，该容器装载着已经被访问过的节点，被访问过的节点不能再次被访问

图搜索优化的方向就是：
按照什么规则去访问节点，按照什么规则弹出节点，使我们尽可能快的找到终止节点。

图遍历算法：

• 广度优先搜索
• 深度优先搜索

广度优先搜索 遵循先进先出的原则，维护的是一个队列

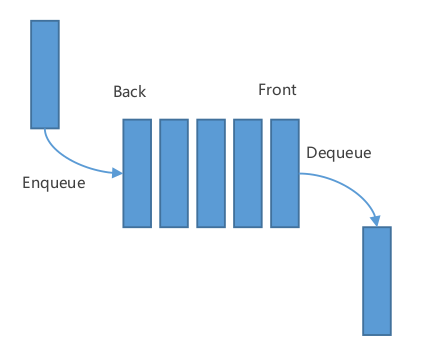
弹出元素，总是从队列的头弹出的
深度优先搜索 遵循的是后进先出的原则，维护的是一个堆栈

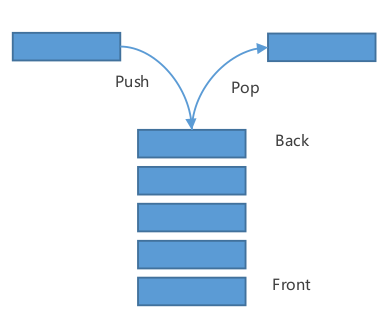
弹出从最上面弹出，最后进入容器的，最先被弹出来