本文探讨深度学习中经常会提到的概念–梯度消失与梯度爆炸。他们是影响模型收敛,学习好坏的一个重要因素,对此现象也提出了对应的解决方案。在此记录其概念,原因和相关的解决方案,仅供参考。
目录
- 概念
- 原因
- 解决方案
- 1. 参数初始化
- 2. 梯度裁剪(Gradient Clipping)
- 3. 正则化
- 4. 激活函数
- 4.1. Relu函数
- 4.2 LeakyRelu函数
- 4.3 ELU函数
- 4. Batch Normalization
- 5. 残差结构
- 6. LSTM网络
概念
梯度爆炸就是在梯度更新时偏导数很大,导致更新参数无法收敛到最值(总会跳到其他不好的地方)。
梯度消失就是在梯度更新时偏导数很小,导致更新参数无法收敛到最值(训不动)。
参数更新公式:
w
=
w
−
α
∂
J
(
w
)
∂
w
w = w-\alpha\frac{\partial J(w)}{\partial w}
w=w−α∂w∂J(w)
原因
主要原因有三点,反向传播在网络较深时出现梯度累积,激活函数的导数,权重初始化参数过小或过大。
- 训练方式:在反向传播的链式求导过程中,如果权重乘以激活函数导数这部分大于1,随着层数加深时,梯度更新会以指数的形式增加,则会梯度爆炸;如果这部分小于1,随着层数加深,梯度会指数衰减,则会出现梯度消失。
- z = wx+b a= σ ( z ) \sigma(z) σ(z) a-> y ^ \hat{y} y^ L( y ^ \hat{y} y^,y)
- 对于某一层:da/dx = da/dz * dz/dx =(激活函数导数)✖️w 得到da/dx 用于梯度传播
- dw = da/dz * x x就是[dz/dw] 用于更新本层的权重参数
- 这一层的dx相当于下一层的da 则继续相乘计算下一层的dx
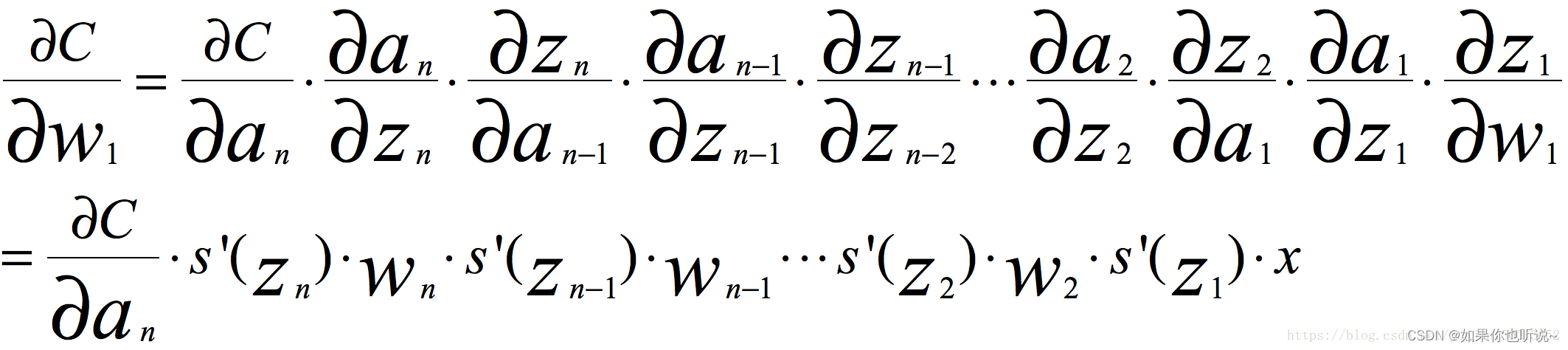
-
激活函数:如果选用sigmoid激活函数, S ( x ) = 1 1 + e − x S(x) = \frac{1}{1+e^{-x}} S(x)=1+e−x1,值在0到1之间。其导数为 S ′ ( x ) = e − x ( 1 + e − x ) 2 = S ( x ) ( 1 − S ( x ) ) S^{'}(x) = \frac{e^{-x}}{(1+e^{-x})^2} =S(x)(1-S(x)) S′(x)=(1+e−x)2e−x=S(x)(1−S(x)),导数最大值为0.25,因此很容易梯度消失。
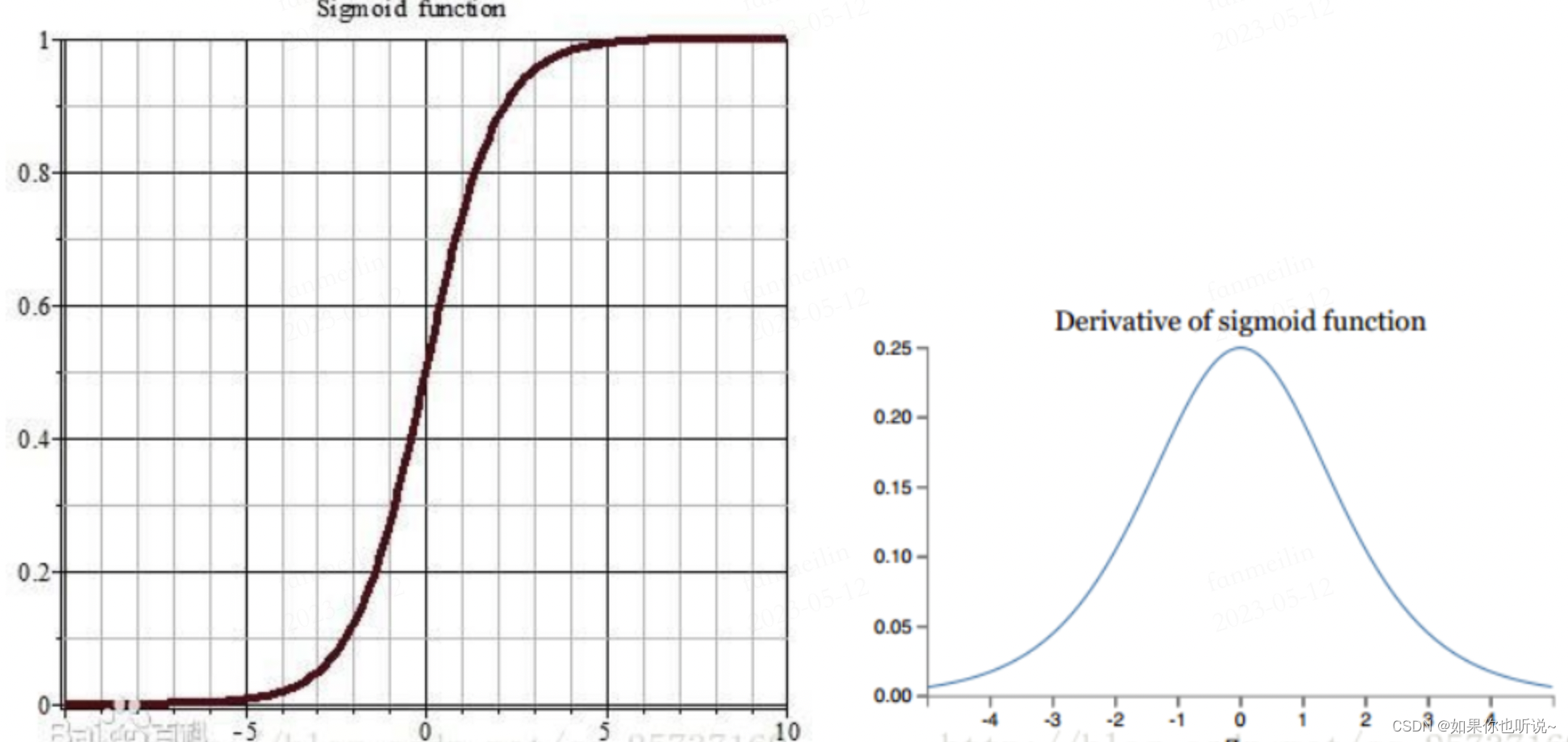
-
权重初始值:一般会使用均值为0方差为1的高斯分布初始化参数,这种方式使得权重集中在-1到1之间,因此很容易出现梯度消失。如果初始化的值很大,就会出现梯度爆炸。
解决方案
1. 参数初始化
可以采用好的参数初始化方法,比如He方法,对梯度爆炸和梯度消失都有作用。具体来说,使得前向传播时,每一层卷积计算结果的方差为1.在反向传播时,每一层向前传的梯度方差为1。
与Xavier方法一样,希望初始化后正向传播时,状态值方差保持不变,反向时,关于下一层激活值的梯度方差保持不变。初始化方法:nl表示l层的神经元个数。
W
∼
N
(
0
,
2
n
l
)
W \sim N(0,\sqrt{\frac{2}{n_l}})
W∼N(0,nl2)
2. 梯度裁剪(Gradient Clipping)
这种方式是解决梯度爆炸的一种高效的方法,这里简单介绍一下对梯度的L2范数进行裁剪,L2范数也就是对所有参数的偏导数求平方和再开方。
设定裁剪阈值为C=max_norm,
∥
g
∥
2
=
g
1
2
+
g
2
2
+
.
.
\Vert g \Vert _2=\sqrt{g^2_1+g^2_2+..}
∥g∥2=g12+g22+..,当其小于C时不变;当其大于C时,进行裁剪,具体公式如下:
g
=
C
∥
g
∥
2
⋅
g
g = \frac{C}{\Vert g \Vert _2} \cdot g
g=∥g∥2C⋅g
3. 正则化
采用权重正则化主要目的是限制过拟合,但也可以抑制梯度爆炸,比较常见的是L1正则,L2正则;
在各个深度框架下有相应的API可以使用正则化;比如在pytorch中的优化器有一个自带的参数weight_decay,用于指定权重衰减率,相当于L2正则化的
α
\alpha
α参数:
L
o
s
s
=
(
y
−
W
T
X
)
+
α
∥
W
∥
2
Loss = (y-W^TX)+\alpha {\Vert W \Vert}^2
Loss=(y−WTX)+α∥W∥2
针对优化器的weight_decay参数,官网解释
weight_decay (float, optional): weight decay (L2 penalty) (default: 0)
optimizer = optim.Adam(model.parameters(),lr=learning_rate,weight_decay=0.01)
4. 激活函数
4.1. Relu函数
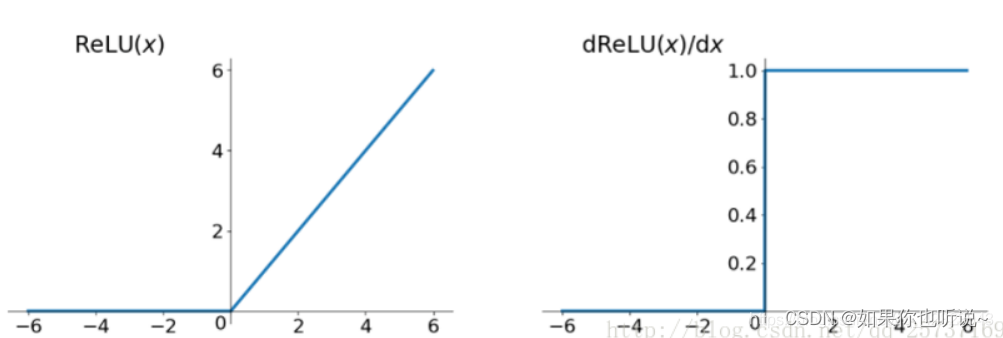
如果激活函数的导数为1,每层网络都尽量获得相同的更新速度,
- 其贡献主要是缓解梯度消失和梯度爆炸;计算方便;加速网络训练。
- 缺点是负数部分恒为0,导致一些神经元完全失活(可通过设置小学习率部分解决);输出不是以0为中心。
4.2 LeakyRelu函数
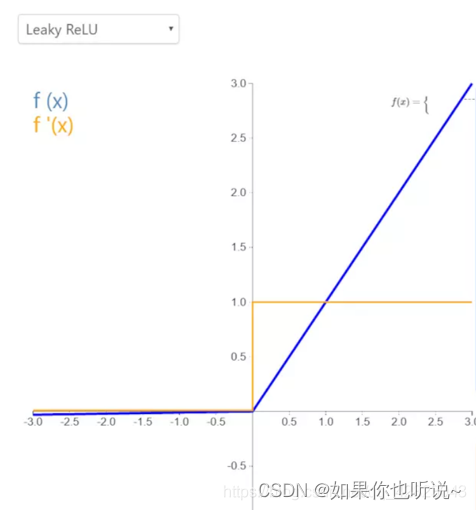
LeakyReLU就是为了解决ReLU的0区间带来的影响,该函数输出对负值输入有很小的坡度,由于导数总是不为零,这能减少静默神经元的出现,允许基于梯度的学习(虽然会很慢),解决了ReLU函数进入负区间后,导致神经元不学习的问题。
4.3 ELU函数
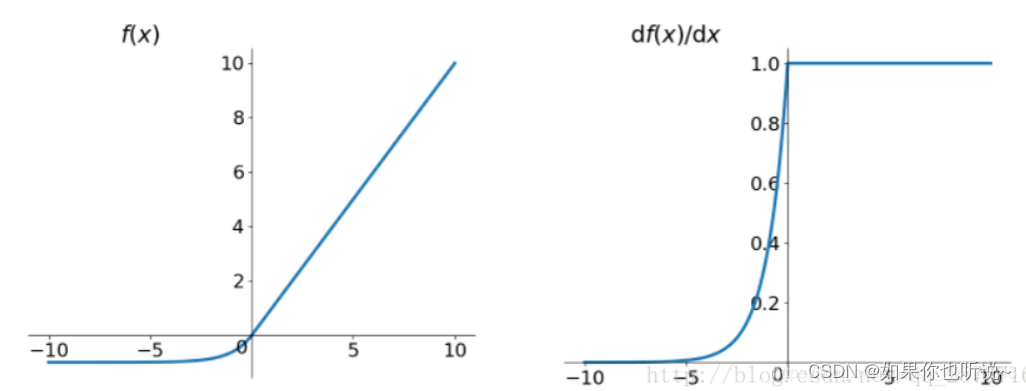
- 融合了Sigmoid和Relu,左侧具有软饱和性,右侧无饱和性;
- 右侧线性部分可以缓解梯度消失,而左侧软饱和可以使得对输入变化和噪声更加鲁棒。
梯度饱和常常是和激活函数相关的,比如sigmod和tanh就属于典型容易进入梯度饱和区的函数,即自变量进入某个区间后,梯度变化会非常小,表现在图上就是函数曲线进入某些区域后,越来越趋近一条直线,梯度变化很小,梯度饱和会导致训练过程中梯度变化缓慢,从而造成模型训练缓慢
4. Batch Normalization
BN是深度学习发展以来提出的最重要的成果之一了,目前已经被广泛的应用到了各大网络中,具有加速网络收敛速度,提升训练稳定性的效果,BN本质上是解决反向传播过程中的梯度问题。BN全名是Batch Normalization,简称BN,即批规范化,通过规范化操作将输出信号x规范化保证网络的稳定性。
反向传播式子中有w的存在,所以w的大小影响了梯度的消失和爆炸,BN就是通过对每一层的输出规范为均值和方差一致的方法,消除了w带来的放大缩小的影响,进而解决梯度消失和爆炸的问题,或者可以理解为BN将输出从饱和区拉倒了非饱和区。
有关Batch Normalization详细的内容可以参考这篇博客:BN原理和代码详解
5. 残差结构
在这里是可以解决梯度消失的问题。
事实上,就是残差网络的出现导致了image net比赛的终结,自从残差提出后,几乎所有的深度网络都离不开残差的身影,相比较之前的几层,几十层的深度网络,在残差网络面前都不值一提,残差可以很轻松的构建几百层,一千多层的网络而不用担心梯度消失过快的问题,原因就在于残差的捷径(shortcut)部分。原理可参见:详解残差网络
6. LSTM网络
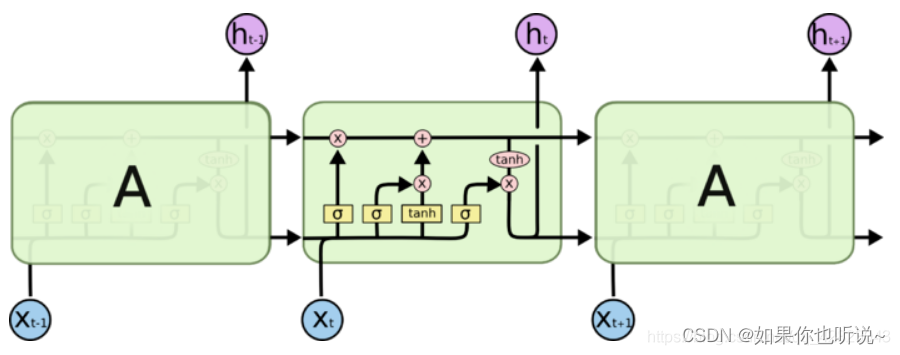
这里也是缓解梯度消失。
LSTM是循环神经网络RNN的变体,全称是长短期记忆网络(long-short term memory networks),它是不那么容易发生梯度消失的,主要原因在于LSTM内部复杂的“门”结构,LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的“残留记忆” ,因此,经常用于生成文本中。LSTM解释