目录
一、准备工作
1.1 下载MASS扩展包与crabs对象
1.2 准备与调整系统内建state相关的对象
1.3 准备mtcars对象
二、了解数据的唯一值
三、基础统计知识与R语言
3.1 数据的集中趋势
3.1.1 认识统计学名词——平均数
3.1.2 认识统计学名词——中位数
3.1.3 认识统计学名词——众数
3.2 数据的离散程度
3.2.1 认识统计学名词——标准差、方差
3.2.2 认识统计学名词——极差
3.3.3 认识统计学名词——四分位数
3.3.4 认识统计学名词——百分位数
3.3 数据的统计
3.3.1 计数值
3.3.2 table对象
3.3.3 计算占比
3.3.4 再看众数
3.4.5 which.max()函数
四、使用基本图表认识数据
4.1 绘制直方图
4.1.1 设定直方图的标题
4.1.2 设定直方图的矩形数
4.2 绘制密度图
4.3 在直方图内绘制密度图
五、认识数据汇集整理函数summary()
六、绘制箱形图
七、数据的相关性分析
7.1 iris对象数据的相关性分析
7.2 stateUSA对象数据的相关性分析
7.3 crabs对象数据的相关性分析
八、使用表格进行数据分析
8.1 简单的表格分析与使用
8.2 从无到有建立一个表格数据
8.3 分别将矩阵与表格转成数据框
8.4 边际总和
8.5 计算数据的占比
8.6 计算行与列的数据占比
一、准备工作
1.1 下载MASS扩展包与crabs对象
crabs数据框是澳大利亚收集的公、母（参杂蓝、橘2色）各100只螃蟹，共计200只的测量数据。
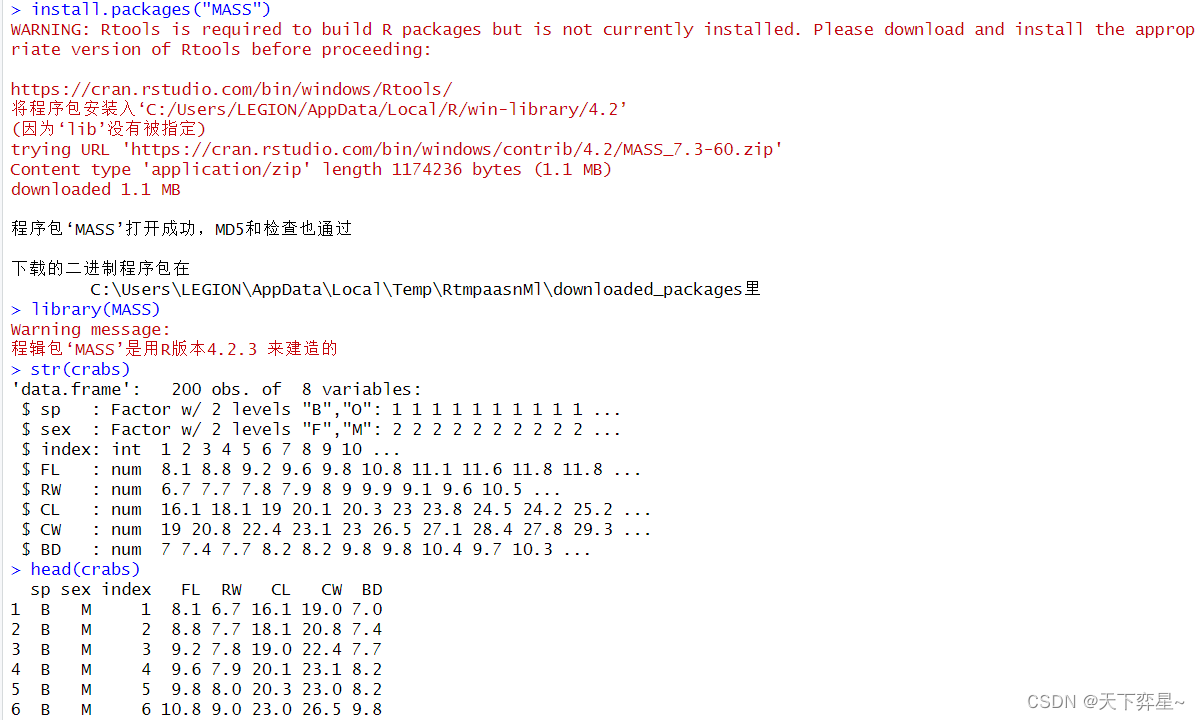
其中sex字段是公母，CL是螃蟹甲壳长度，CW是螃蟹甲壳宽度。
1.2 准备与调整系统内建state相关的对象
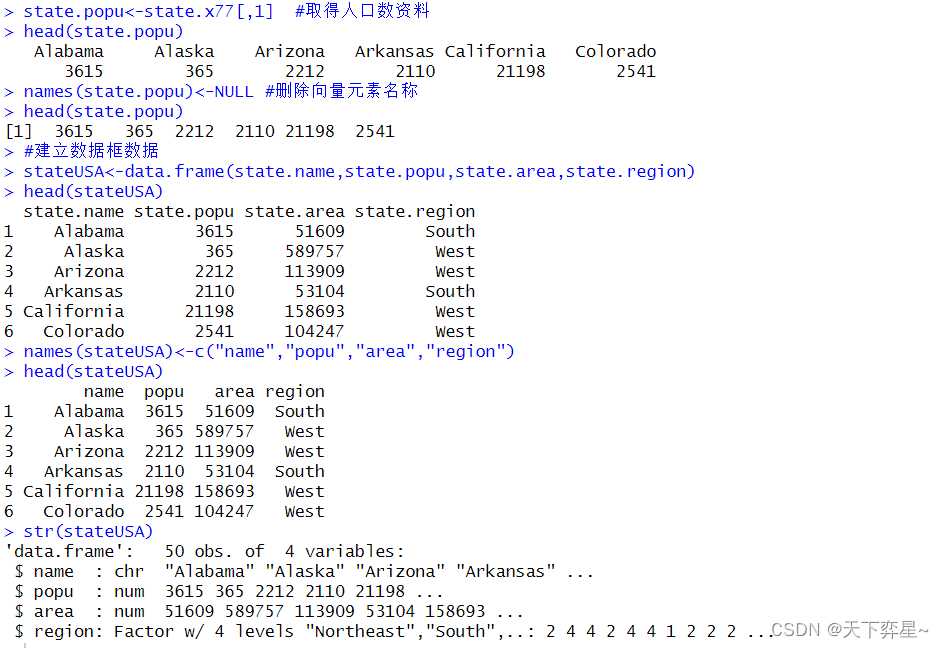1.3 准备mtcars对象
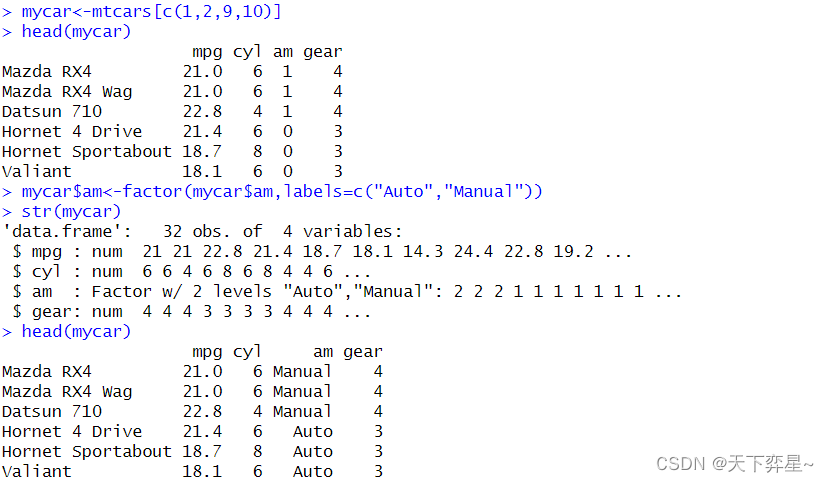
二、了解数据的唯一值
对于某些数据框的变量字段的数据元素而言，到底是以数值呈现还是以因子呈现较好，完全视所需要分析的数据类型而定，基本原则是若数据可以当作分类数据，则可以考虑改成因子。另外，也可以由数据的唯一值的计数判断，一般计数值少的字段也适合改成因子。
三、基础统计知识与R语言
对于大量的数据集我们多会研究两个基本性质，一个是集中趋势，另一个是离散程度。
3.1 数据的集中趋势
通常数据会聚集在中位数附件，这样的模式就被称为集中趋势，中位数也可以看作是数据的中心代表，常被用来测量集中趋势的指标有以下三种：平均数、中位数、众数。
3.1.1 认识统计学名词——平均数
所谓的平均数是指在一个数据集中，所有观察值的总和除以观察值总个数所得的数值。
在R语言中，可以使用mean()函数获得平均值。
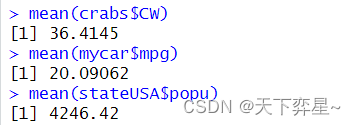
3.1.2 认识统计学名词——中位数
所谓中位数是指一组可排序的数据中，将数据切成后50%及前50%的值（或是最中间的值），也就是将数据排序以后恰好有一半的数据大于中位数，也恰有一半的数据小于或等于中位数。简单说如果数据量是奇数，最中间的数字就是中位数；如果数据量是偶数，则最中间的两个数字的平均值就是中位数。在R语言中，可以使用median()函数获得中位数。
3.1.3 认识统计学名词——众数
所谓众数是指在数据集中，出现次数最多的值。R语言中目前没有求众数的函数。
3.2 数据的离散程度
衡量离散（变化）程度的标准有标准差、方差、极差、四分位数、百分位数等。
3.2.1 认识统计学名词——标准差、方差
sd()：标准差函数。
var()：方差函数。
3.2.2 认识统计学名词——极差
所谓极差是指数据集中最大观察值减掉最小观察值所得的数值，实际上可想成数据的范围。
事实上R语言提供了range()函数，可列出数据的最大值与最小值。
3.3.3 认识统计学名词——四分位数
所谓四分位数是指将数据集（由小到大）分成4等份的三个数值，其中第1个四分位数通常为第25%的数值，第2个四分位数也就是中位数（通常为第50%的数值），而第3个四分位数通常为第75%的数值。我们可以利用quantile()函数取得这些值。
对上述实例而言，共有8个数据，所以第2个四分位数也就是中位数，序位的计算为(8+1)/2=4.5，也就是第4个数据和第5个数据的平均值，得到的结果为(11+23)/2=17；第1个四分位数（也就是25%）的序位数是由序位的最小值1与中位数的序位数4.5取平均数，即(1+4.5)/2=2.75，再由第2个数据和第3个数据取内插求得，所以是(3+0.75*(5-3))，得到的结果是4.5，依此类推。
3.3.4 认识统计学名词——百分位数
所谓百分位数是指将数据由大到小等分为100份的数值，我们一样是可以使用quantile()函数计算此百分位数。
3.3 数据的统计
3.3.1 计数值
计数主要应用在数据框内的因子中，计算某个因子元素的数据出现的次数或称频率。我们常用table()函数执行这个任务，也可以将这个table()函数的返回结果称为频率表。
3.3.2 table对象
table()函数产生了表格数据"table"，这个结果与一维数组相同，对于数组数据而言，可以有一到多维的表格，每个维度的表格又可以有各自的名称。
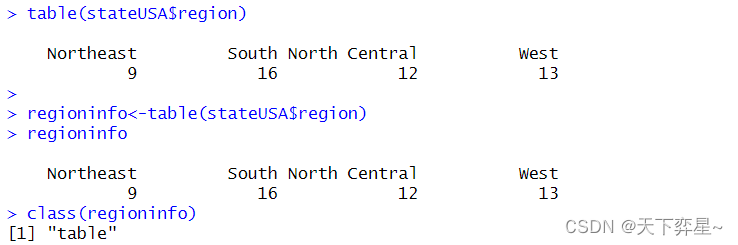
3.3.3 计算占比
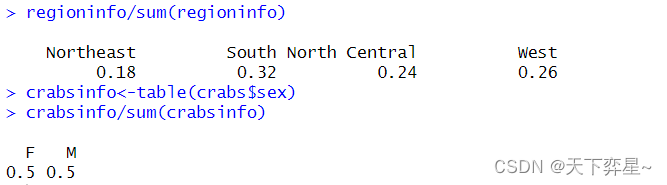
3.3.4 再看众数
众数不是唯一的，如果发生出现次数相同情况，这些元素都将是众数。
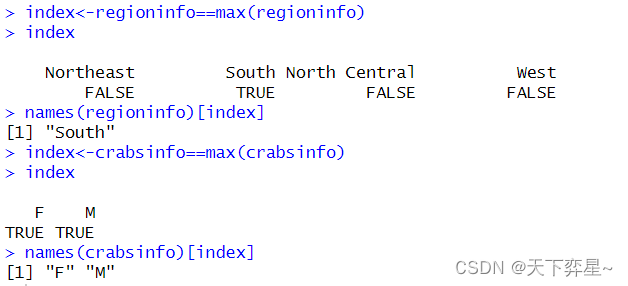
3.4.5 which.max()函数
R语言中提供了which.max()函数，可以求得对象的最大值，我们也可以使用这个函数的最大值求众数。
which.max()函数将只传回第1个数据。
四、使用基本图表认识数据
4.1 绘制直方图
直方图是根据数据分布情况，自动选择有利于表现数据的柱宽作为x轴间隔，以频数（或称计数）或者百分比作为y轴的一系列连接起来的数据分布图。直方图的优点是不论数据样本数量的多寡都能使用直方图。
注：使用R语言绘制数据图时，若使用PC的Windows系统则可以在数据图内加注中文字，但目前在数据图内加注中文字的功能并不支持macOS系统上的R语言环境。
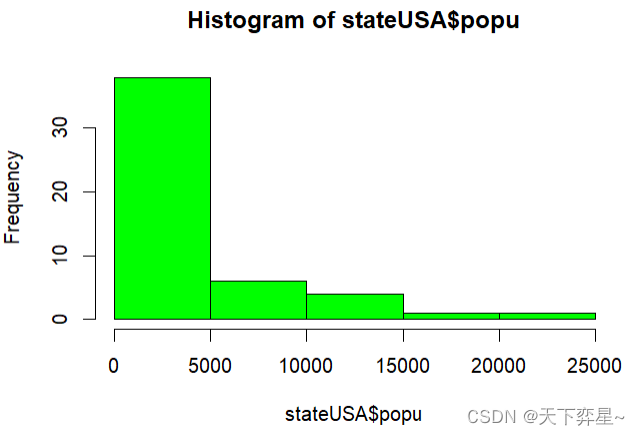
上述图形的主标题、x轴和y轴标题均是默认的。
4.1.1 设定直方图的标题
其实在hist()函数中，可以加上下列参数。
main：图表标题。
xlab：x轴标题。
ylab：y轴标题。
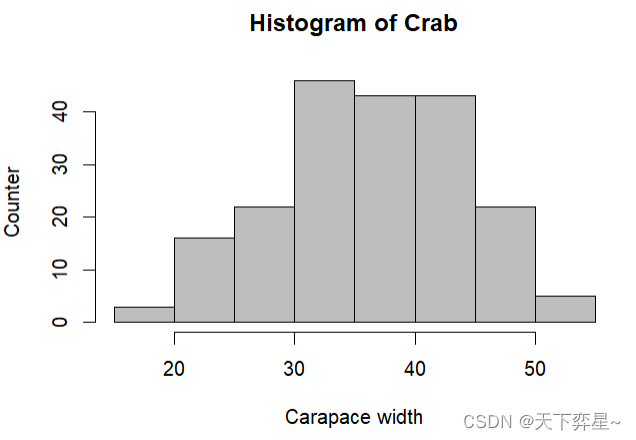
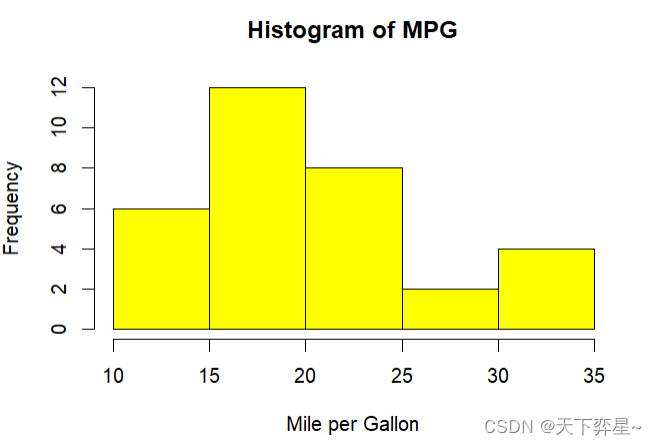
4.1.2 设定直方图的矩形数
在hist()函数内，可以直接指定直方图矩形的数量。
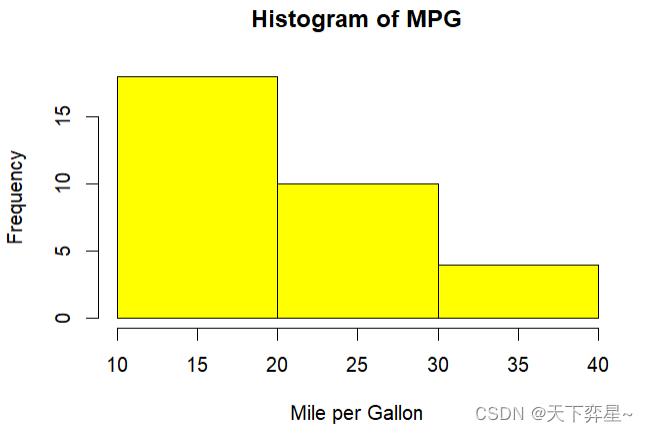
另外，也可以直接使用breaks参数，设定矩形的区间。
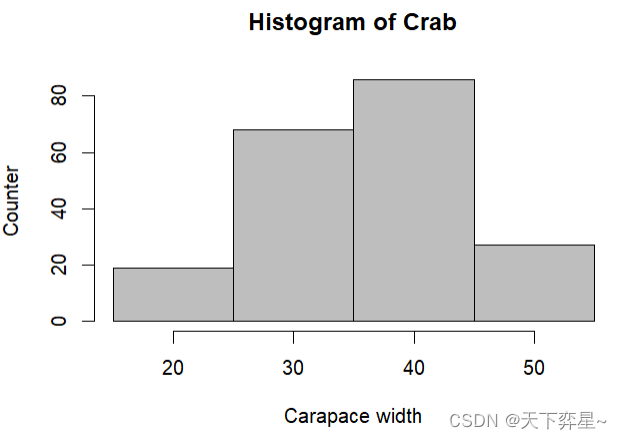
4.2 绘制密度图
R语言有提供密度函数density()，可以将欲建图表的数据利用这个函数转成一个密度对象列表，然后将这个对象放入plot()函数内就可以绘制密度图。
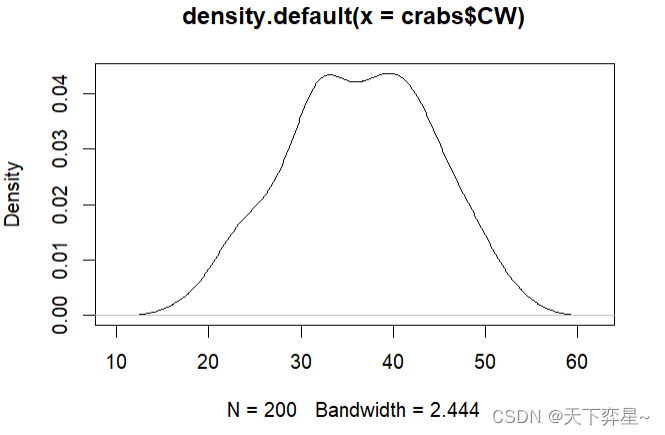
与hist()函数一样，可以使用下列参数设置图的标题。
main：图表标题。
xlab：x轴标题。
ylab：y轴标题。
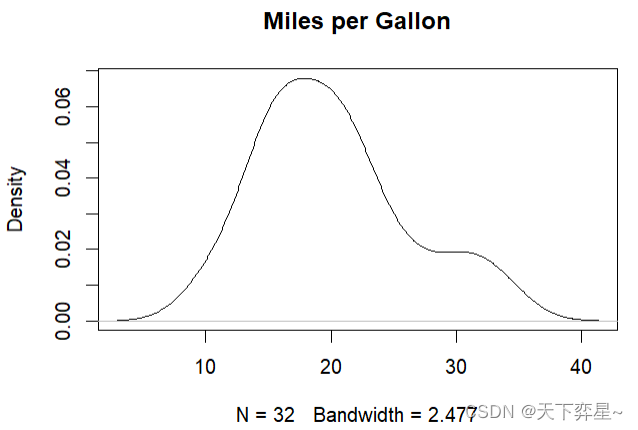
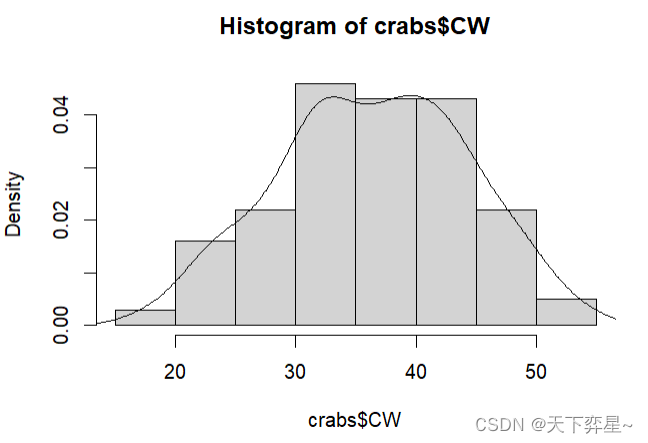
4.3 在直方图内绘制密度图
R语言允许在直方图内加上密度图，若想达到这个目标，在使用hist()函数时，需增加下列参数。
freq=FALSE然后执行下列函数：
lines()
五、认识数据汇集整理函数summary()
summary()函数可以传回数据分布的信息。
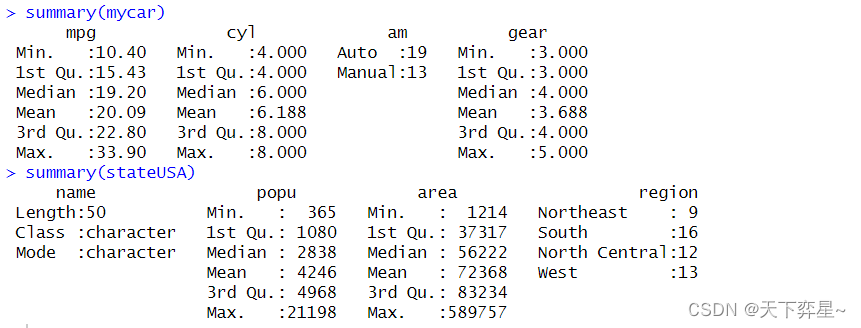
由上述两个实例，我们可以获得下列信息：
（1）数值变量：会列出最小值、最大值、平均值、第1个四分位值、中位值（也可想成第2个四分位数）、第3个四分位值。如果有NA值，也会列出NA值的数量。
（2）因子：列出频率表，如果有NA值，也会列出NA值得数量。
（3）字符串变量：列出字符串长度。
在上述两个实例中，对stateUSA对象使用summary()函数后所获得得结果是完美得。但仔细看对mycar对象使用summary()函数后得输出结果，在cyl变量和gear变量中均可发现最小值和第1个四分位值相同，为了避免这种状况，在以后碰到类似得数据时，只要将他们转成因子即可。
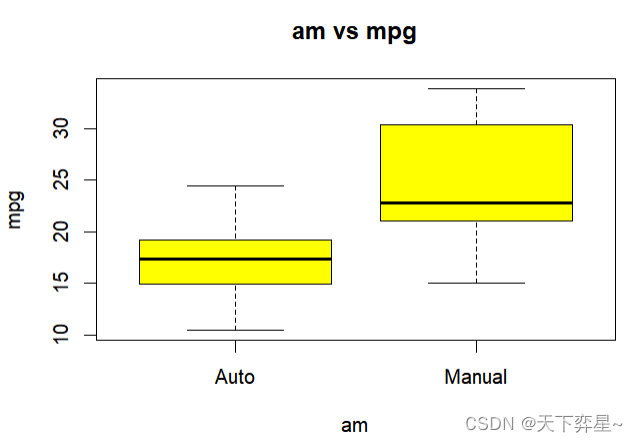
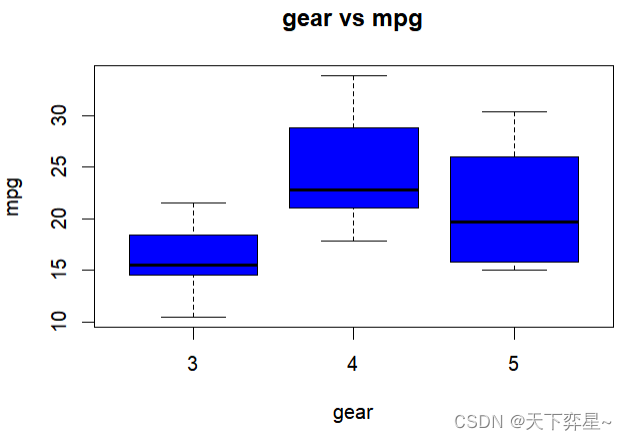
六、绘制箱形图
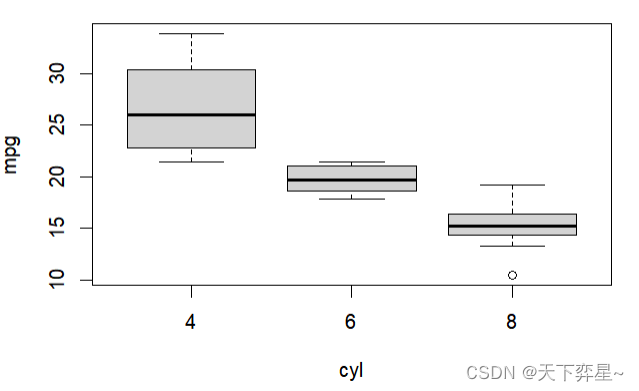
上述boxplot()函数得第1个参数，如下所示，其实是一个公式。
mpq~cyl其意义是与变量cyl类别（可想成气缸数）相关得mpg数值，将被带入boxplot()函数中运算，而箱形图各线条意义如下所示：
- 箱子上下边缘线条：代表上四分位数和下四分位数。
- 横向贯穿箱子粗线条：中位数。
- 纵向贯穿箱子的线条：是最大值与最小值或是上下四分位间距离的1.5倍。
之前使用的main参数仍可以用在这里，用于列出箱形图的标题，"col="参数仍可用于产生彩色箱形图。
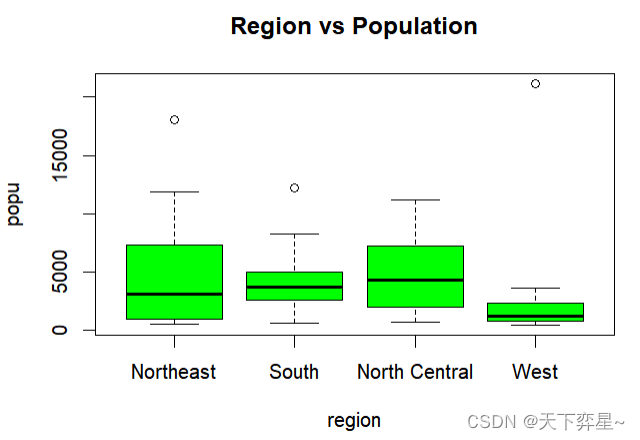
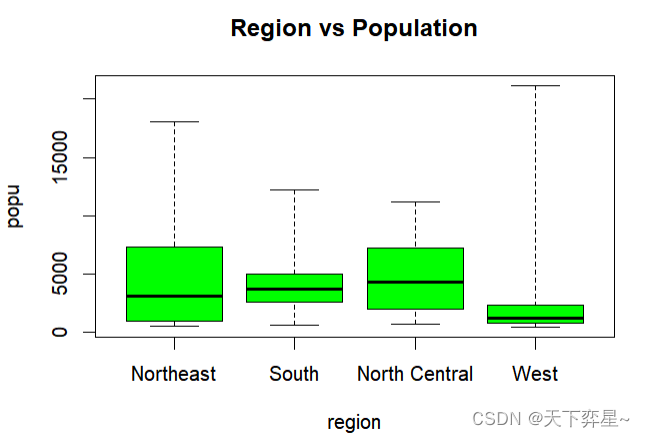
其实如果仔细看上述箱形图，可以看到Northeast、South和West上方有空心原点，那才是真正的线段的最大值（在其他实例中也许会在线段下方看到空心圆点，此时是代表线段的最小值），若是希望箱形图线段指向最大或最小值，可以在boxplot()函数加上参数"range=0"。
七、数据的相关性分析
统计学中，用于反映两个变量向量的相关程度的指标称为相关系数，相关系数的数值在-1至1之间；越靠近1的相关系数数值代表正相关越强，而越靠近-1的相关系数数值代表负相关性越强；而靠近在0附近则表示两变量之间的线性相关是相对微弱的。
7.1 iris对象数据的相关性分析
在R语言中，想要了解相关性系数可以使用cor()函数。
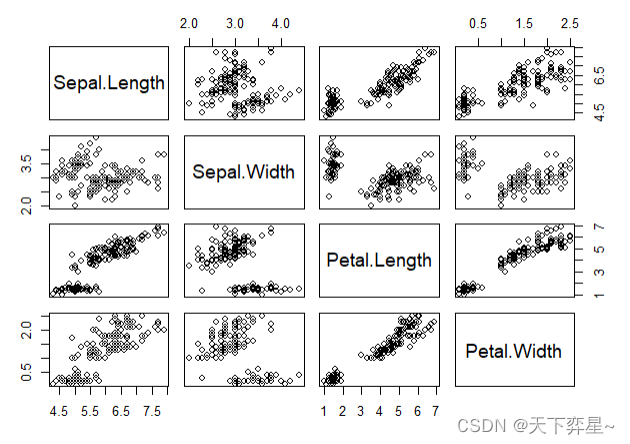
我们可以利用plot()函数，绘出两两不同变量间的相关系数散点图。
在上述实例中，使用plot()函数执行绘制散点图的任务。当发现所传入的参数是数据框时，调用pairs()函数也可以执行绘制散点图的任务。
最后使用cor()函数需考虑数据中有NA值的情形，此时需使用参数"use="，其基本方法如下：
- 参数use="everything"是默认值，若是向量变量元素中有NA，则该元素的计算结果也是NA。
- 参数use="complete"，不处理NA值，此时只计算非NA值的部分。
- 参数use="pairwise"，对变量内有NA值的向量不予计算。
7.2 stateUSA对象数据的相关性分析
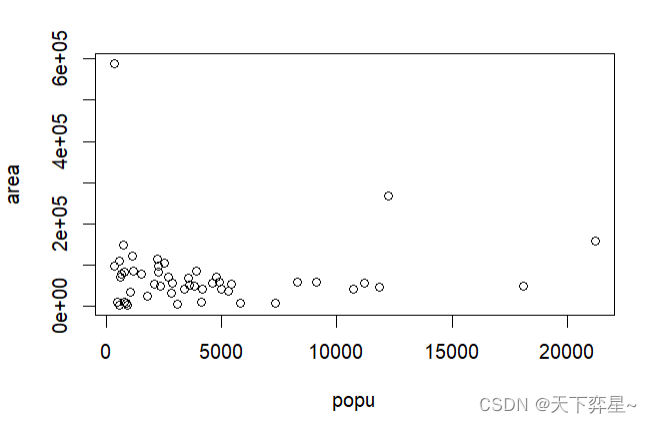
7.3 crabs对象数据的相关性分析
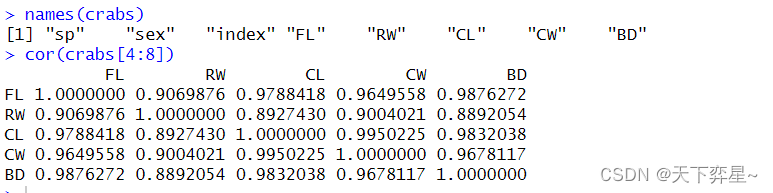
八、使用表格进行数据分析
8.1 简单的表格分析与使用
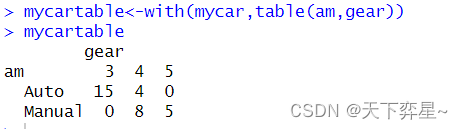
8.2 从无到有建立一个表格数据
8.3 分别将矩阵与表格转成数据框
8.4 边际总和
在数据分析过程中，我们很可能会对表格的行或列进行加总运算，所得值我们称为边际总和，我们可以使用以下函数：
addmargins(A,margin)A：表格数据或数组。
margin：若省略则列与行皆计算，若为1则计算“列”，所以“行”会增加Sum字段，若为2则计算“行”，所以“列”会增加Sum字段。
8.5 计算数据的占比
R语言中提供的prop.table()函数可以计算数据的占比。
上述计算的是在全部受测者中的比例。
8.6 计算行与列的数据占比
利用prop.table()函数时，也可以通过增加参数margin，实现只针对行和列做计算。
