数组-稀疏矩阵的转置
第1关:一般转置算法
任务描述
本关任务:实现稀疏矩阵的转置操作(采用一般转置算法,即按列序转置)。
相关知识
为了完成本关任务,你需要理解:1. 矩阵的压缩存储,2.稀疏矩阵的三元组顺序表存储表示,3.一般转置算法。
矩阵的压缩存储
矩阵的压缩存储是指:为多个值相同的非零元素只分配一个存储空间,对零元素不分配空间,从而节省存储空间。
稀疏矩阵的三元组顺序表存储表示
稀疏矩阵是指非零元素的个数远远少于总的元素个数,且非零元素的分布没有规律。
稀疏矩阵的压缩存储就是只存储非零元素;且存储非零元素的值的同时,还需存储其所在的行和列。
于是,将非零元所在的行、列及其值构成一个三元组(i,j,v),且按行优先方式排列三元组,从而构成稀疏矩阵的三元组线性表,称为三元组表。
三元组表的存储方式有顺序存储和链式存储,从而可引出稀疏矩阵的两种压缩存储方式:三元组顺序表存储和十字链表存储。
//三元组顺序表存储表示
#define MAXSIZE 100
typedef int datatype;
typedef struct
{
int i,j;
datatype v;
}SPNode; //三元组类型
typedef struct
{
int m,n,t; //矩阵的总行数、总列数及非零元个数
SPNode data[MAXSIZE];
}SPMatrix;
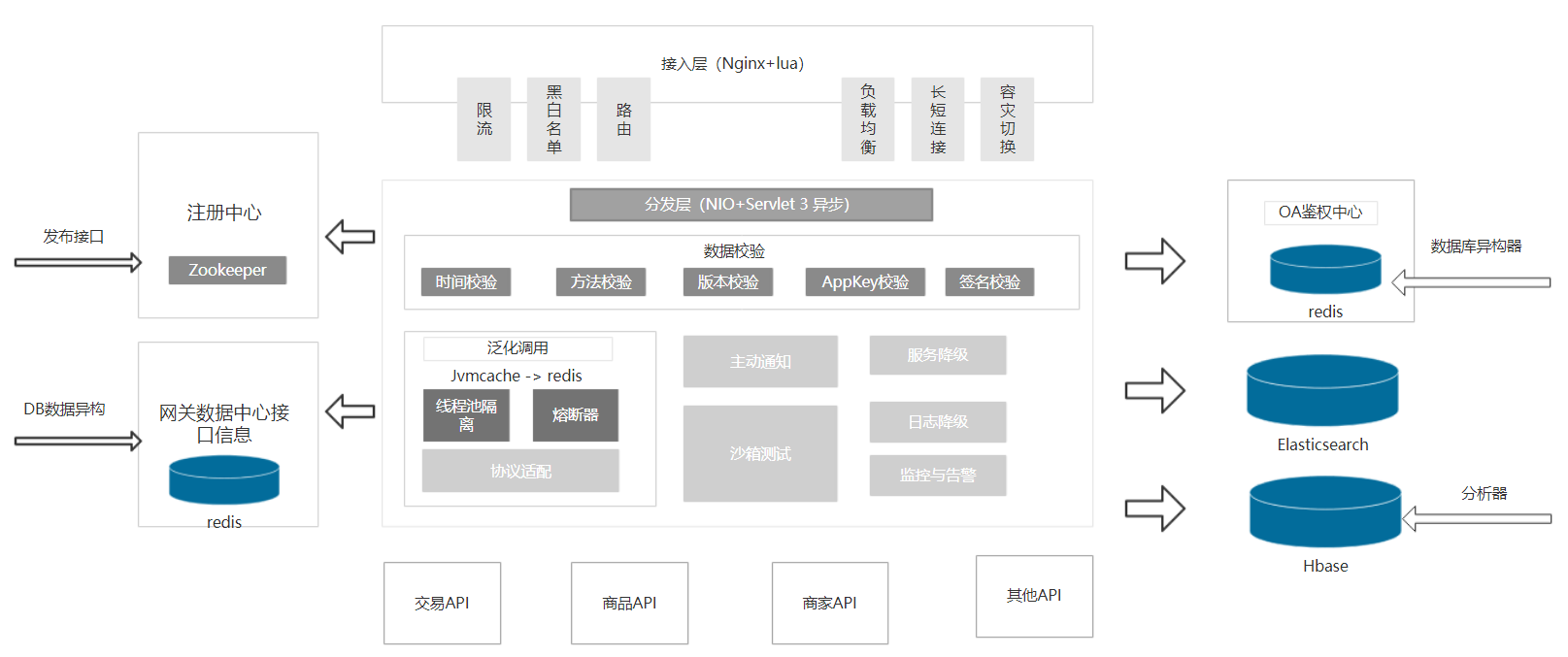
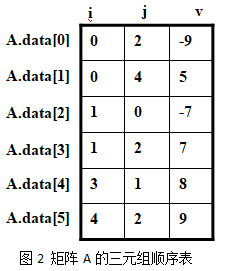
如:下面图1所示的稀疏矩阵A的三元组顺序表的数据存储情况如图2所示。

一般转置算法
先在矩阵A的三元组表A.data中找到第0列的非零元素存入转置阵B的三元组表B.data中,再找到第1列存入B.data中,……,这样得到的转置矩阵B的三元组表B.data中的元素必定按行优先存放。
如何在A.data中找第k列?
需对A.data扫描一遍,即:先比较A.data[0].j是否等于k,若相等,则将A.data[0]存入B.data中,接着继续比较下一个A.data[1].j, …… 。
编程要求
在右侧编辑器中补充代码,完成TransSMatrix函数,以实现稀疏矩阵的转置操作。具体要求如下:
* TransSMatrix:求稀疏矩阵A的转置阵B,采用一般转置算法(即按列序转置),稀疏矩阵采用三元组顺序表存储。
测试说明
平台会对你编写的代码进行测试,测试文件为step1/Main.cpp,可在右侧文件夹中进行查看。
输入输出格式: 输入格式: 第一行输入矩阵A的总行数、总列数及非零元个数 第二行按行序输入矩阵A的各个非零元素的行号、列号及值 输出格式: 先输出矩阵A的三元组表,再输出A的转置阵的三元组表。末尾换行。
测试输入:
5 5 6 //输入矩阵A的总行数、总列数及非零元个数
0 2 -9 0 4 5 1 0 -7 1 2 7 3 1 8 4 2 9 //按行序输入矩阵A的各个非零元素的行号、列号及值
预期输出:
The Matrix A:
(0,2,-9)
(0,4,5)
(1,0,-7)
(1,2,7)
(3,1,8)
(4,2,9)
The Transport Matrix of A:
(0,1,-7)
(1,3,8)
(2,0,-9)
(2,1,7)
(2,4,9)
(4,0,5) //末尾换行
开始你的任务吧,祝你成功!
代码示例
/*************************************************************
稀疏矩阵 实现文件
更新于2020年10月28日
**************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "SparseMatrix.h"
void input(SPMatrix &a)//输入采用三元组顺序表存储的矩阵
{
int p;
scanf("%d%d%d",&a.m,&a.n,&a.t); //输入矩阵总行数、总列数和非零元素的个数
for(p=0;p<a.t;p++)
scanf("%d%d%d",&a.data[p].i,&a.data[p].j,&a.data[p].v);
}
void output(SPMatrix a)//输出矩阵的三元组表
{
int p;
for(p=0;p<a.t;p++)
printf("(%d,%d,%d)\n",a.data[p].i,a.data[p].j,a.data[p].v);
}
void TransSMatrix(SPMatrix a, SPMatrix &b)//一般转置,即:按列序转置
{
// 请在这里补充代码,完成本关任务
/********** Begin *********/
b.m=a.n;
b.n=a.m;
b.t=a.t;
if (b.t) {
int q=0; //三元组表T的下标
int p; //三元组表M的下标
for (int col=0;col<=a.m; col++) { //从最小列顺序开始找
for (p=0; p<a.t; p++) { //从三元组表M顺序查找
if (a.data[p].j==col) { //三元组表M中当前列是最小列,则进行转置
b.data[q].i=a.data[p].j;
b.data[q].j=a.data[p].i;
b.data[q].v=a.data[p].v;
q++;
}
}
}
}
/********** End **********/
}
第2关:快速转置算法
任务描述
本关任务:实现稀疏矩阵的转置操作(采用快速转置算法)。
相关知识
为了完成本关任务,你需要理解:1. 稀疏矩阵的三元组顺序表存储表示,2.快速转置算法。
稀疏矩阵的三元组顺序表存储表示
//三元组顺序表存储表示
#define MAXSIZE 100
typedef int datatype;
typedef struct
{
int i,j;
datatype v;
}SPNode; //三元组类型
typedef struct
{
int m,n,t; //矩阵的总行数、总列数及非零元个数
SPNode data[MAXSIZE];
}SPMatrix;
快速转置算法
一般转置算法效率低的原因是通过对A.data扫描若干遍来找到第0列,第1列,……,共需扫描n遍。我们如果能直接确定A中每一个三元组在B中的位置,则对A.data扫描一遍即可。那么,如何确定A中每一个三元组在B.data中的位置?
设两个数组x[n]和y[n]。其中,x[i]表示A中第i列的非零元的个数,y[i]初始值表示A中第i列第一个非零元在B.data中的位置。
显然有:
y[0]=0
y[1]=y[0]+x[0]
……
y[i]=y[i-1]+x[i-1]
接下来依次扫描A.data,先判断A.data[0],取出A.data[0].j用变量k保存(k=A.data[0].j),表示该三元组是A中第k列第一个非零元,则其在B.data中的位置为q=y[k],接着将该三元组存入B.data[q]中,然后y[k]++,以便将第k列的下一个非零元存放到B.data下一个位置;接着再判断A.data[1],……。
编程要求
在右侧编辑器中补充代码,完成FastTransSMatrix函数,以实现稀疏矩阵的转置操作。具体要求如下:
* FastTransSMatrix:求稀疏矩阵A的转置阵B,采用快速转置算法,稀疏矩阵采用三元组顺序表存储。
测试说明
平台会对你编写的代码进行测试,测试文件为step2/Main.cpp,可在右侧文件夹中进行查看。
输入输出格式: 输入格式: 第一行输入矩阵A的总行数、总列数及非零元个数 第二行按行序输入矩阵A的各个非零元素的行号、列号及值 输出格式: 先输出矩阵A的三元组表,再输出A的转置阵的三元组表。末尾换行。
测试输入:
5 5 6 //输入矩阵A的总行数、总列数及非零元个数
0 2 -9 0 4 5 1 0 -7 1 2 7 3 1 8 4 2 9 //按行序输入矩阵A的各个非零元素的行号、列号及值
预期输出:
The Matrix A:
(0,2,-9)
(0,4,5)
(1,0,-7)
(1,2,7)
(3,1,8)
(4,2,9)
The Transport Matrix of A:
(0,1,-7)
(1,3,8)
(2,0,-9)
(2,1,7)
(2,4,9)
(4,0,5) //末尾换行
开始你的任务吧,祝你成功!
/*************************************************************
稀疏矩阵 实现文件
更新于2020年10月28日
**************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "SparseMatrix.h"
void input(SPMatrix &a)//输入采用三元组顺序表存储的矩阵
{
int p;
scanf("%d%d%d",&a.m,&a.n,&a.t); //输入矩阵总行数、总列数和非零元素的个数
for(p=0;p<a.t;p++)
scanf("%d%d%d",&a.data[p].i,&a.data[p].j,&a.data[p].v);
}
void output(SPMatrix a)//输出矩阵的三元组表
{
int p;
for(p=0;p<a.t;p++)
printf("(%d,%d,%d)\n",a.data[p].i,a.data[p].j,a.data[p].v);
}
void FastTransSMatrix(SPMatrix a, SPMatrix &b)//快速转置
{
int p,q,i,k; int x[N],y[N];
b.m=a.n; b.n=a.m; b.t=a.t;
if(b.t==0)
{
printf("The matrix has no nonzero element!\n"); return;
}
for(i=0;i<a.n;i++) x[i]=0;
for(p=0;p<a.t;p++) //求A中每一列非零元个数存放到x[ ]中
{
/********** Begin *********/
int k=a.data[p].j;
x[k]++;
/********** End **********/
}
y[0]=0;
y[1]=y[0]+x[0];
for(i=2;i<a.n;i++)//求A中每一列的第一个非零元在B.data中的位置存放到y[ ]中
{
/********** Begin *********/
y[i]=y[i-1]+x[i-1];
/********** End **********/
}
for(p=0;p<a.t;p++) //扫描A.data,将A中每一三元组存放到B中恰当位置
{
/********** Begin *********/
int i=a.data[p].j;
int q=y[i];
b.data[q].i=a.data[p].j;
b.data[q].j=a.data[p].i;
b.data[q].v=a.data[p].v;
y[i]++;
/********** End **********/
}
}