一、小小算法的魅力

这是一个很普通的小例子，但是可以让我们领略到算法改进之后的强大魅力。

已知a+b+c = 1000，且a^2+b^2=c^2，求a、b、c的所有自然数解。
这个很简单，就是通过代码分别给a、b、c赋值，然后返回符合a+b+c = 1000且a^2+b^2=c^2的解。
这里有两段参考代码如下：
第一段就是按照一般的试错逻辑，分别遍历1~1000赋值给a、b、c，然后通过条件if a + b + c == 1000 and a**2 + b**2 == c**2取出符合的三个值。

# 代码1：
import time
start_time = time.time()
for a in range(1,1001):
    for b in range(1,1001):
        for c in range(1,1001):
            if a + b + c == 1000 and a**2 + b**2 == c**2:
                print('a:%d, b:%d, c:%d'%(a,b,c))
end_time = time.time()
print('程序总用时：%f'%(end_time-start_time))

代码1的执行结果如下图，本次的执行时间是951.8秒。

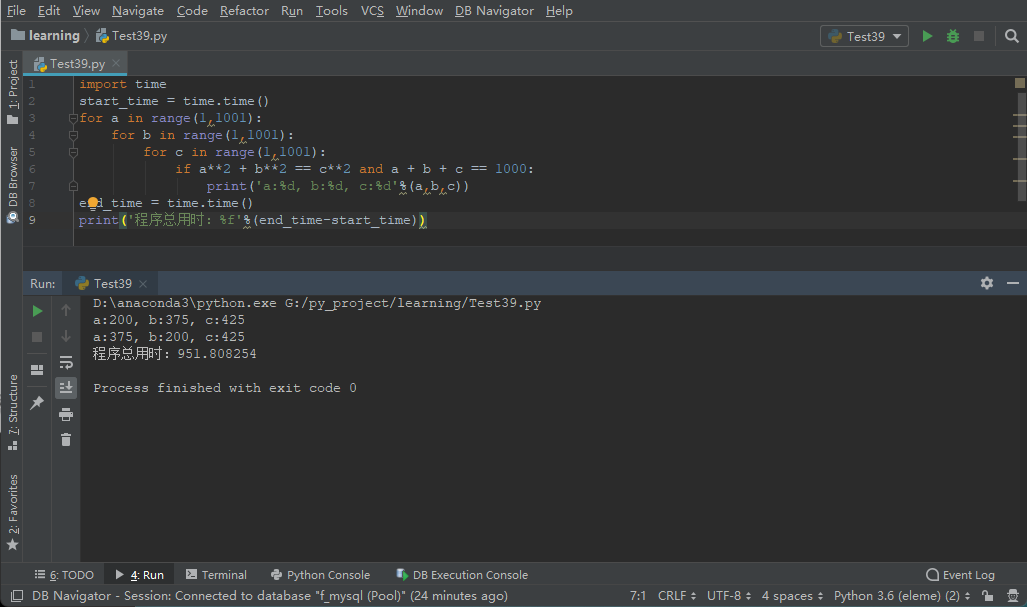
再来看看代码2，在代码1的基础上做了一个小改动，只遍历两次1~1000，第三个数通过1000减去前两个数得到，代码如下：

# 代码2：
import time
start_time = time.time()
for a in range(1,1001):
    for b in range(1,1001):
        if a**2 + b**2 == (1000-a-b)**2:
            print('a:%d, b:%d, c:%d'%(a,b,1000-a-b))
end_time = time.time()
print('程序总用时：%f'%(end_time-start_time))

代码2的执行结果如下图，可以看到本次执行该代码只需要1.4秒。

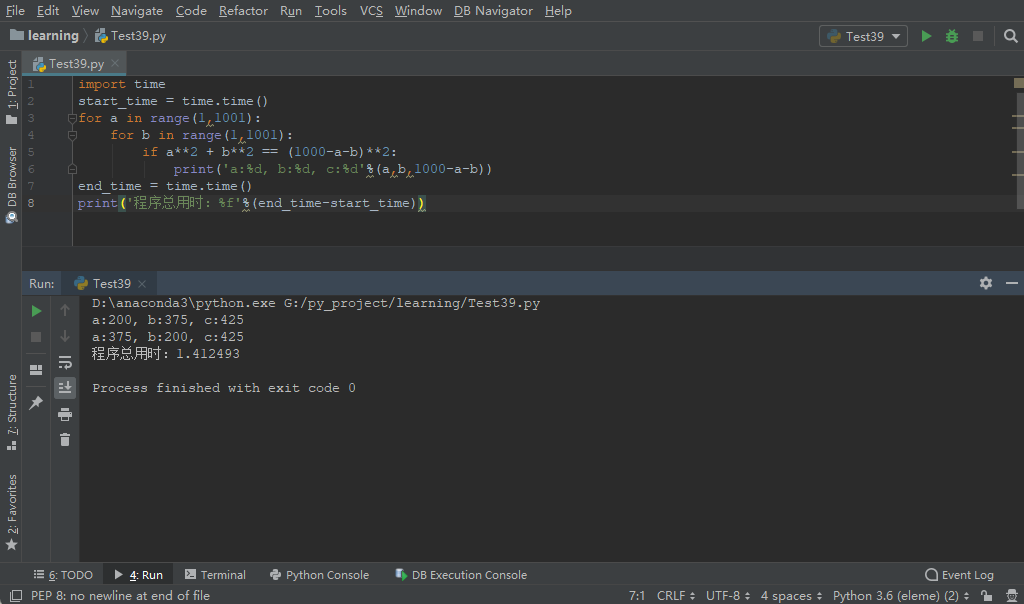
从上面两段代码的执行结果，我们可以看到二者的时间相差700倍左右！用代码2替换代码1，每次执行少等待16分钟左右，这是一种特别好的体验。

感受到算法的小小魅力之后，接下来简单讲讲算法的复杂度问题。

二、复杂度

复杂度一般分为两种：时间复杂度和空间复杂度。
时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间，在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度，所以我们如今已经不需要再特别关注一个算法的空间复杂度，更多关注其时间复杂度。

2.1 时间复杂度

时间复杂度，也是渐进时间复杂度（asymptotic time complexity），官方的定义如下：
若存在函数f(n)，使得当n趋近于无穷大时，$T(n)/f(n)$ 的极限值为不等于零的常数，则称$f(n)$是$T(n)$的同数量级函数。记作$T(n)=O(f(n))$，称$O(f(n))$为算法的渐进时间复杂度，简称时间复杂度。
渐进时间复杂度用大写O来表示，所以也被称为大O表示法。，常见表示方法如$O(1)$、$O(logn)$、$O(n)$、$O(nlogn)$、$O(n^2)$、$O(n^3)$、$O(2^n)$等。
一般情况下，复杂度越小，则说明你的代码越好，复杂度的大小参考如下：
$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$

计算时间复杂度时，理论上需要考虑到所有需要消耗时间的运行操作，比如说遍历一个元素都是长字符串的列表找到相等的字符串，除了考虑遍历字符串的执行时间，还需要考虑字符串的对比（如下例子）。

for i in ['abc','bcd','cde']:
    if i == 'cde':
        print(i)

一般基础代码，不带任何调用其他对象的代码是常数项，有几行就算执行几次；遍历循环则根据序列的长度定义，假设序列长度为n，遍历1次序列则为n，并列遍历2次则为$2\ast n$，嵌套遍历2次则为$n^2$。

不过，在实际应用过程，一般会简化时间复杂度，更多时候只是是看影响最大的因素。

2.2 时间复杂度的简化

在比较时间复杂度时通常会采用以下几个方法进行简化之后对比复杂度：

• 复杂度为常数，使用O(1)表示，如$O(23)$，$O(9999)$；
• 复杂度包含n时，省略系数与常数项， 如：$O(2n+45)⟶O(n)$；
• 复杂度为对数时，用O(logn)表示，如：$lo{g}_{5}n$、$lo{g}_{2}n$；
• 忽略低阶，只取高阶，如$O(4n^3+6n^2+n)⟶O(n^3)$。

如：$logn+nlogn$表示为$O(nlogn)$。

比较时间复杂度的时候，一般会忽略常数项、低阶项、高阶项的系数和log的底数。比如说$O(2n+1)$简化为O(n) ，$O(2\ast n^3+5n^2+5)$简化为$O(n^3)$，$O(lo{g}_{2}n)$简化为$O(logn)$。文章开头的两串代码的复杂度则分别是$O(n^2)$和$O(n^3)$。

2个问题：
1、为什么忽略常数项、低阶项和系数？

• 因为大O其实就是数据量级突破一个点且数据量级非常大的情况下所表现出的时间复杂度，这个点常数项、低阶项和系数已经不起决定性作用。

2、为什么O(logn)不区分对数的底数？

• 因为一个对数可以转化成为一个常数乘以一个其他底的对数，即$lo{g}_{2}16=lo{g}_{10}16/lo{g}_{10}2⟺lo{g}_{10}16=lo{g}_{10}2\ast lo{g}_{2}16$（把16看成是n更有助于下面的理解），所以$O\left(lo{g}_{2}n\right)=lo{g}_{2}10\ast O\left(lo{g}_{10}n\right)⟺O\left(lo{g}_{i}n\right)=lo{g}_{i}j\ast O\left(lo{g}_{j}n\right)$故$O\left(lo{g}_{i}n\right)⟹O\left(lo{g}_{j}n\right)⟹O\left(logn\right)$。

2.3 常见函数的复杂度

常见函数	Big-O
[n], index	O(1)
append()	O(1)
pop()	O(n)
insert()	O(n)
del	O(n)
iteration	O(n)
contain()	O(n)
[m,n] slice	O(m)
del slice	O(n)
set slice	O(n+m)
reverse	O(n)
concaterate	O(m)
sort	O(n log n)
multiply	O(n*m)
copy	O(n)
get items	O(1)
set items	O(1)
del items	O(1)
contains(n)	O(1)
iteration	O(n)

三、小结

1、一般地，在比较时间复杂度时会采用以下几个方法进行简化再对比：

• 复杂度为常数，使用O(1)表示，如$O(23)$，$O(9999)$；
• 复杂度包含n时，省略系数与常数项， 如：$O(2n+45)⟶O(n)$；
• 复杂度为对数时，用O(logn)表示，如：$lo{g}_{5}n$、$lo{g}_{2}n$；
• 忽略低阶，只取高阶，如$O(4n^3+6n^2+n)⟶O(n^3)$。

2、复杂度越小，则说明你的代码越好，复杂度的大小参考如下：
$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$