一.朴素模式匹配
1.机算
其实就是暴力匹配。
使用双指针 i (指向主串) j (指向模式串)
从主串 S 第一字符起,与模式串 T, 第一个字符比较,
①若相同,则 i 与 j 统一向后移
②若遇到 i 与 j 指向字符不同,回溯 i j 指针。继续如此,直至匹配成功j超出模式串,或者 匹配失败 i 超出主串。
2.手算
略。
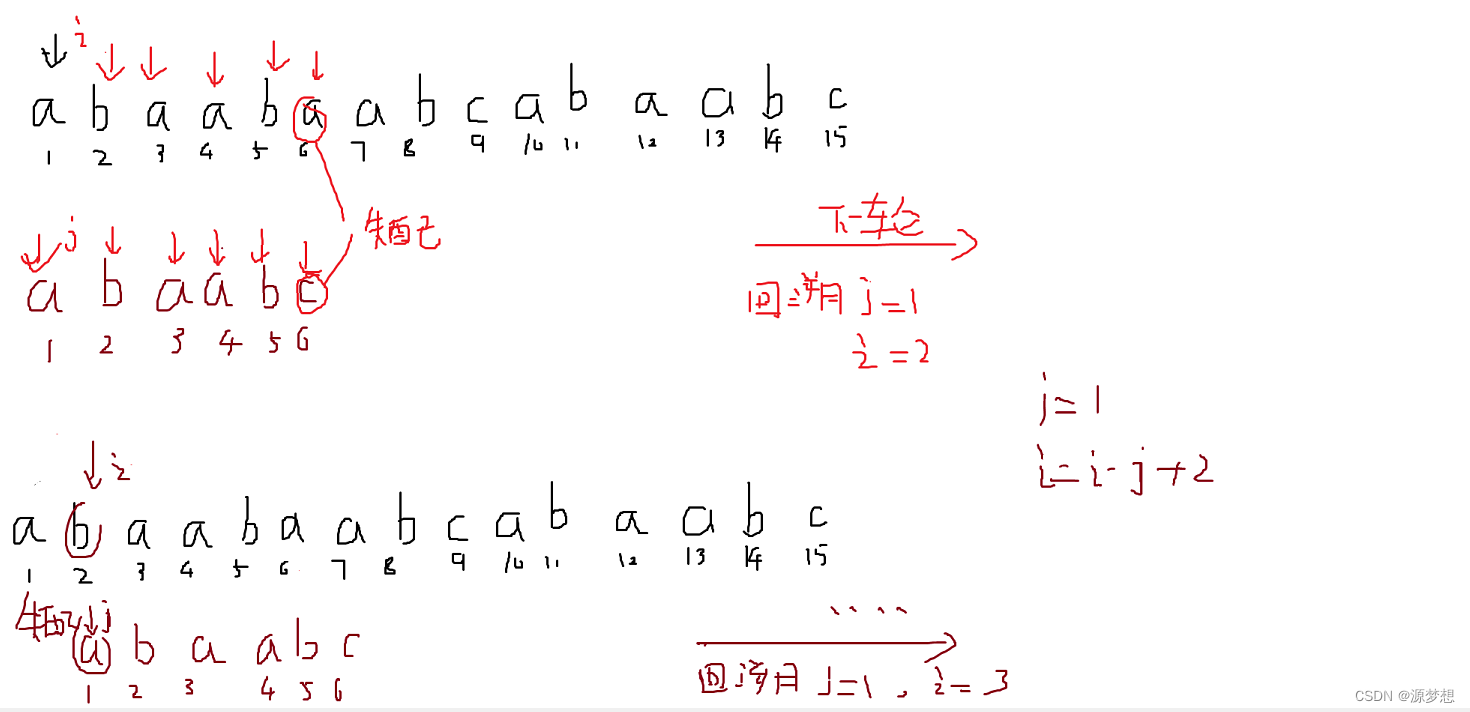
二.KMP next[ ]
1.机算求next [ ] 数组
由于朴素模式匹配中,i j 指针的疯狂回溯,造成了时间复杂度的巨大。
我们可以很明显的观察到,i j 指针很多时候没必要回溯这么狠。
我们是否可以根据 “模式串” 研究出 i j 指针匹配失败时候,回溯的位置?-----next [ ]数组。
略
2.手算求next [ ] 数组
为了对应算法,废弃next[0],直接从next[1]开始存储。
1.第一个与第二个固定,永远都为0 1
next [ 1 ] = 0
next [ 2 ] = 1
2.其他
在不匹配位置前,划一个分界线。模式串一步步向右滑,直到分界线之前能对的上,或模式串完全跨过分界线为止,此时 j 指向的位置即为对应next值。
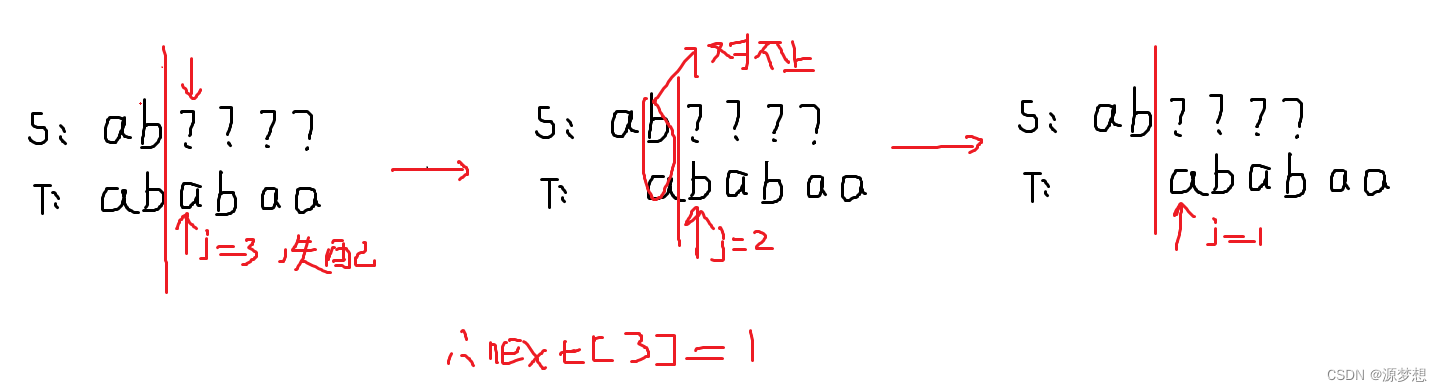
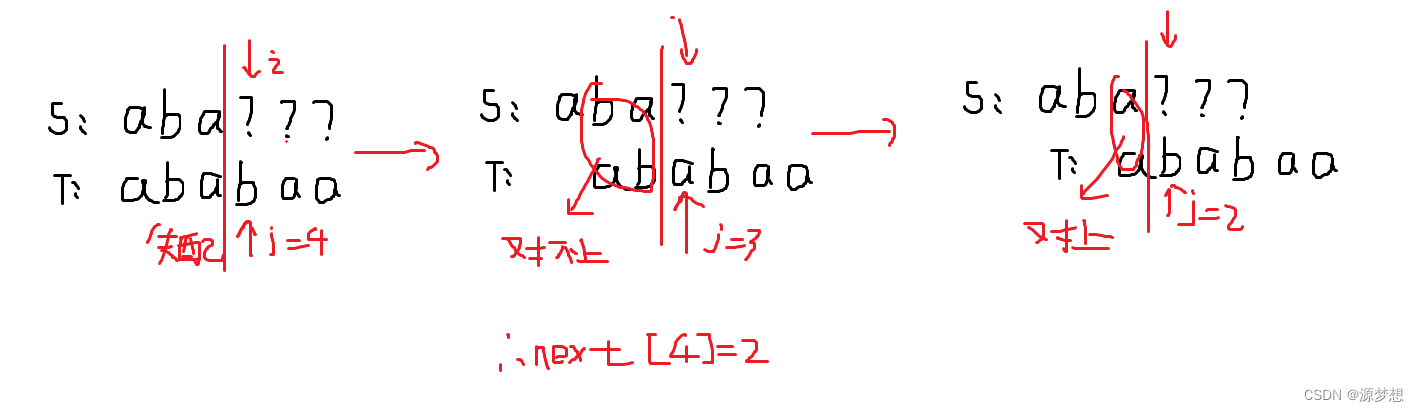
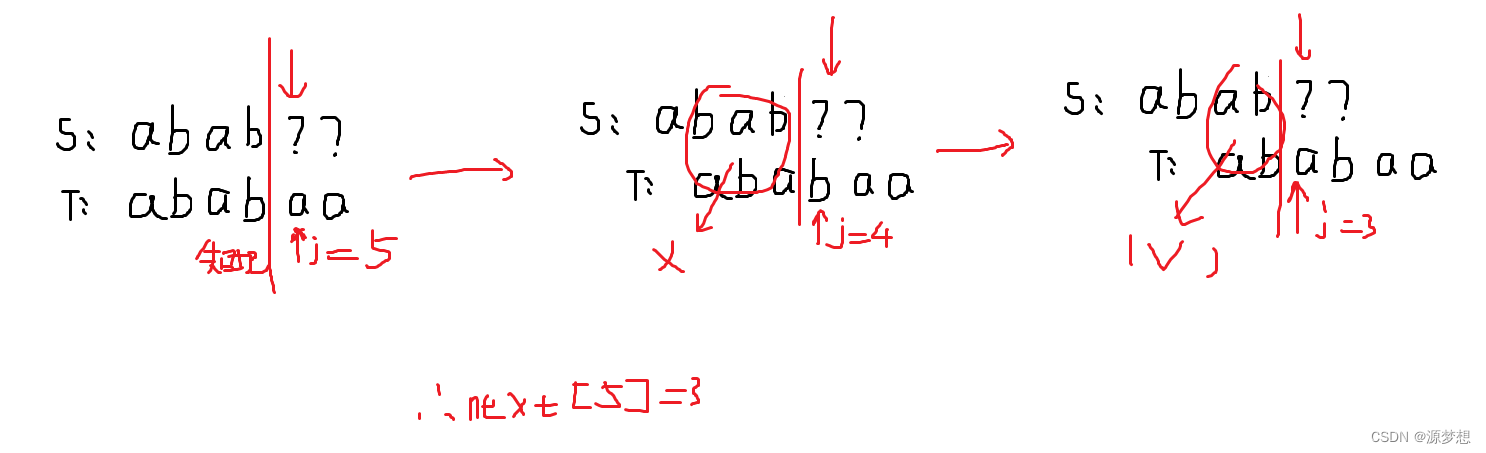
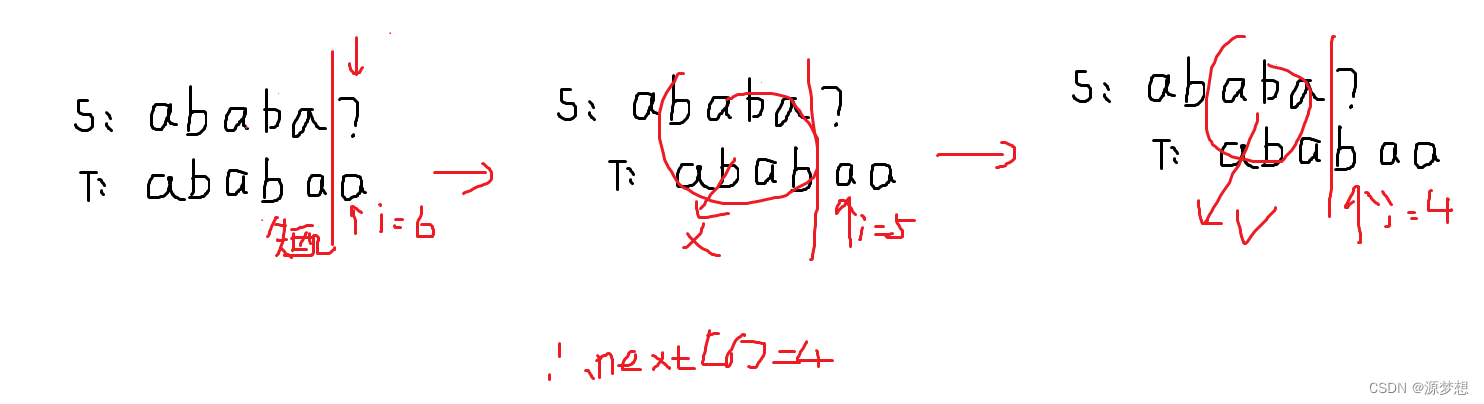
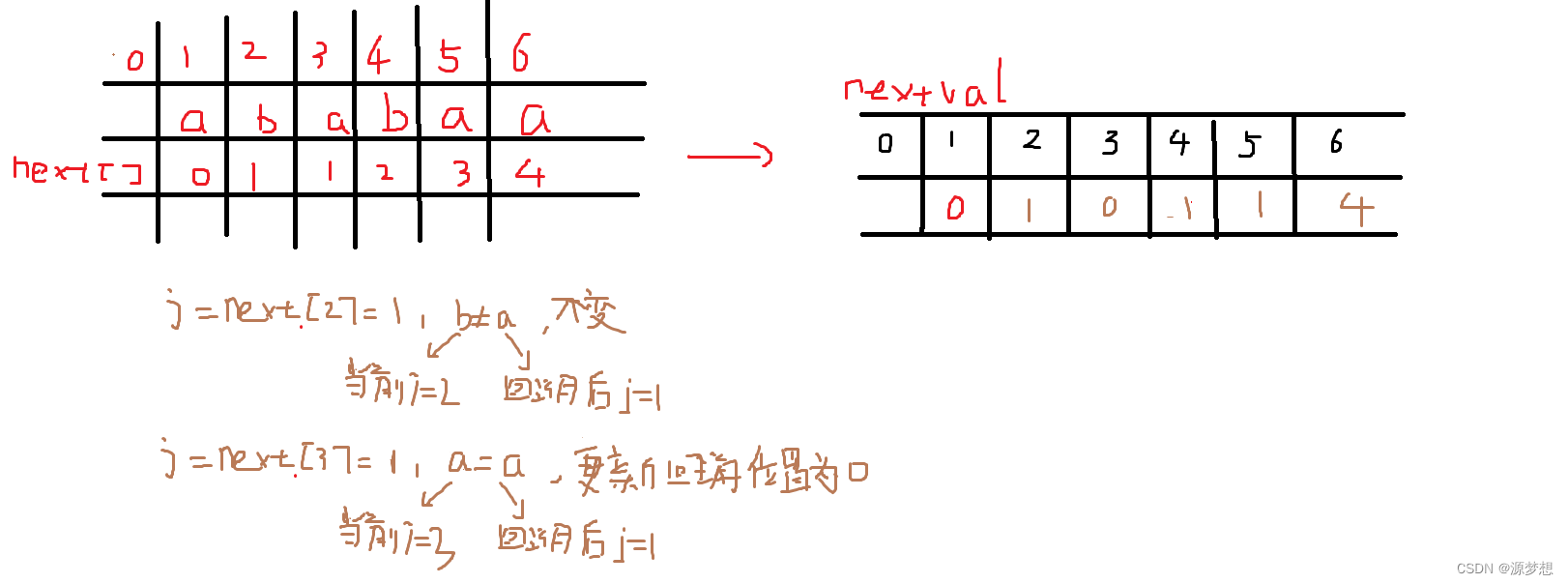
三.KMP优化 nextval[ ]
1.机算求nextval[ ]
有这样情况:
但是本次回溯后的匹配注定是失败的,我们不应该让其匹配,可以让其直接从“第一个失败后 j 指针的位置开始”。
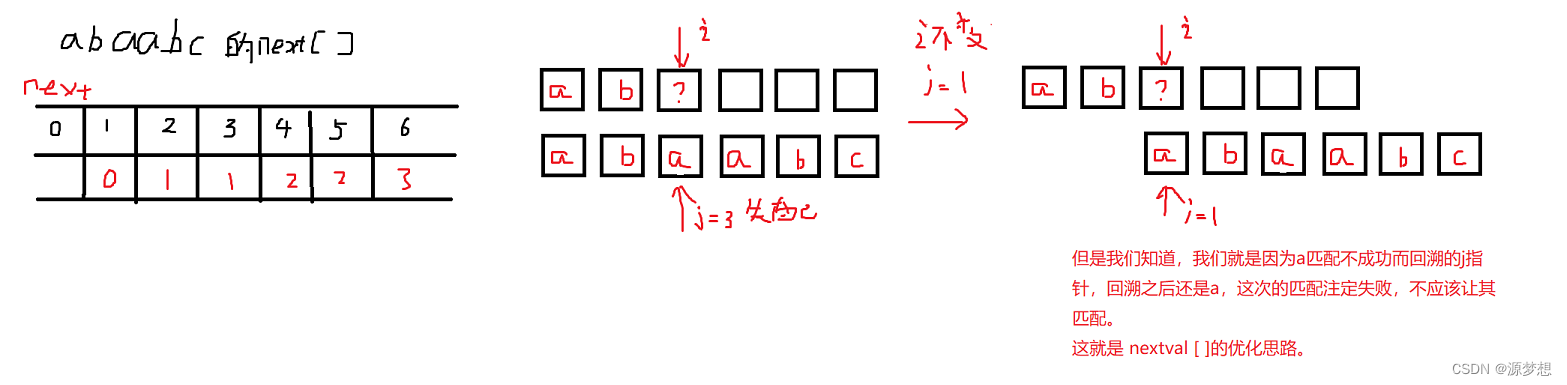
机算求nextvam[ ]略。
2.手算求nextval[ ]
①先求出模式串T 对应的next [ ]数组。
②nextval[ 0 ]舍弃,nextval[ 1 ] = 0.
③如果当前字符与对应next [ j ] 所指字符相等,让 nextval[ j ] = nextval[ next[j] ];
否则 nextval[ j ] = next[ j ]