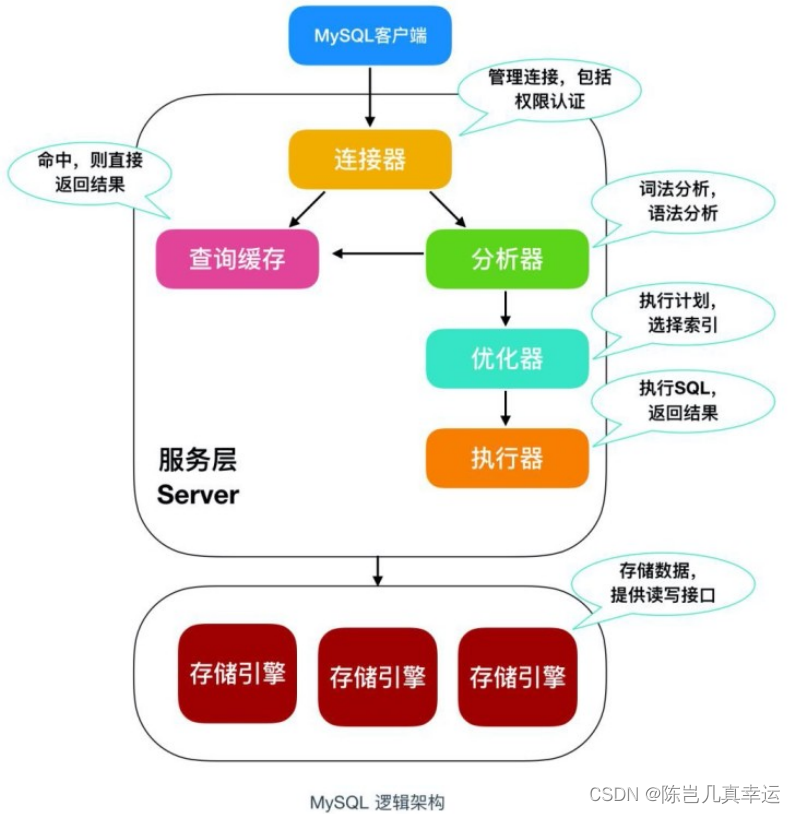
本篇文章重点讨论一般无穷积敛散性的判别。(即被积函数在所积区间符号不定,既有正的,也有负的)
不论是绝对收敛还是条件收敛,它本身一定是
收敛的。
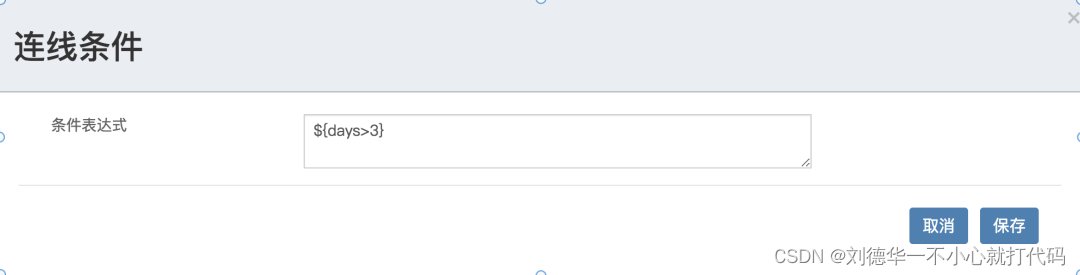
狄利克雷判别法:

例题:
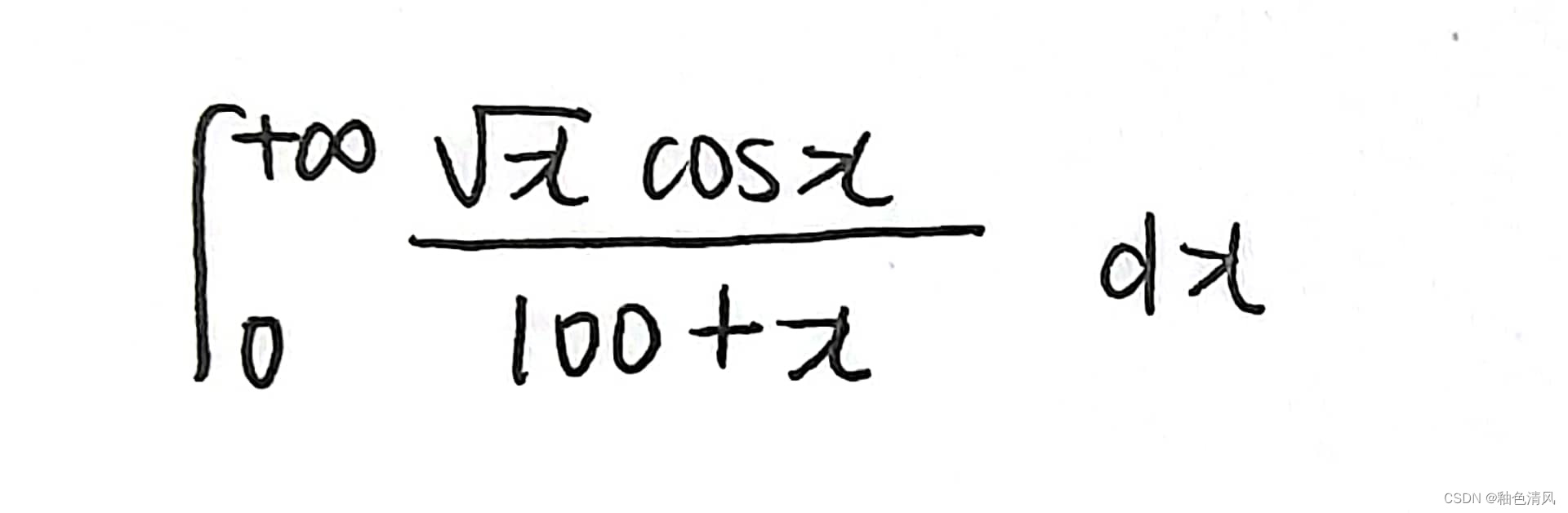
首先,将被积函数写成两个函数的乘积,利用狄利克雷判别法。
即确定f(x)和g(x),①f(x)=cosx,判断cosx在(0,+∞)的积分是否有界②判断g(x),当x趋于+∞时,g(x)是否单调递减趋于0。
完整过程如下:

过程分析:
(1)确定f(x)和g(x),根据判别过程依次判断。
(3)对于三角函数不定积分(不论上限是几),都是有界的,≤2。
(2)对于g(x)的单调性判断,若不能直接判断,则可以进行求导。其次判断当x趋于+∞时,g(x)是否趋于0。
(4)由狄利克雷判别法,得……
(5)判断是条件收敛还是绝对收敛。
练习题1
完整过程如下 
本题,可以分母次数为2,可以直接判断绝对收敛。
练习题2
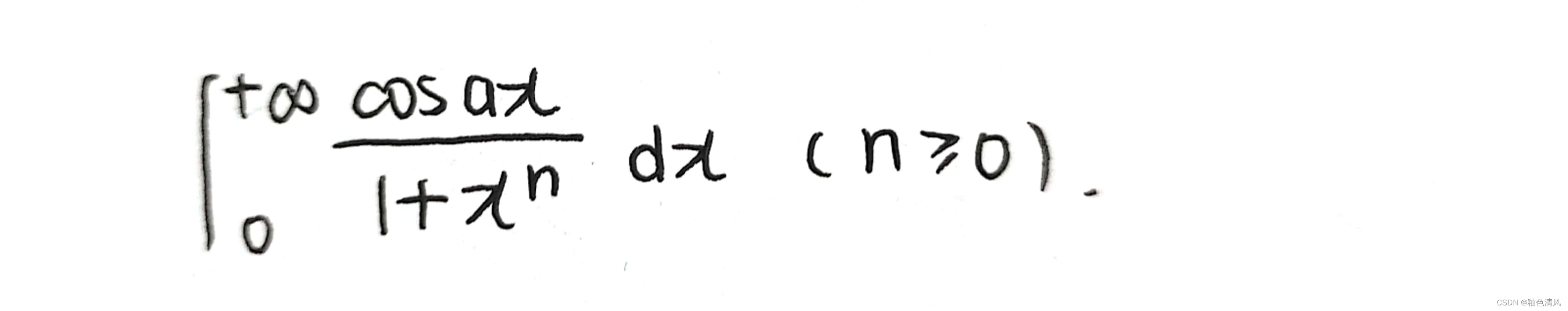
完整过程 如下:

练习题 3

完整过程如下: