二叉树的层序遍历

层序遍历：逐层地，从左到右访问所有节点
广度优先

文章目录

二叉树的层序遍历
- 102. 二叉树的层序遍历 - 力扣（LeetCode）
- 107. 二叉树的层序遍历 II - 力扣（LeetCode）
- 199. 二叉树的右视图 - 力扣（LeetCode）
- 429. N 叉树的层序遍历 - 力扣（LeetCode）
- 515. 在每个树行中找最大值 - 力扣（LeetCode）
- 104. 二叉树的最大深度 - 力扣（LeetCode）
- 111. 二叉树的最小深度 - 力扣（LeetCode）
- 总结
- 扩展

102. 二叉树的层序遍历 - 力扣（LeetCode）

在这里插入图片描述
代码及思路分析

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    // res存储结果  queue队列里面存储每层节点
    let res = [], queue = []
    queue.push(root)
    if(root === null) return res
    
    // 遍历当前层的所有节点
    while(queue.length!== 0) {
        // 记录当前层级节点数
        let length = queue.length
        // 存放每一层的节点
        let curLeverl = []
        for(let i = 0; i < length; i++) {
            // 弹出队列的节点，也就是当层的节点 从左到右
            let node = queue.shift
            // 弹出一个，并且把他的子节点压入队列，为了下一次的遍历
            curLeverl.push(node.val)
            // 存放当前层下一层的节点
            node.left && queue.push(node.left)
            node.right && queue.push(node.right)
        }
        // 把每一层的结果放到结果数组
        res.push(curLeverl)
    }
};

107. 二叉树的层序遍历 II - 力扣（LeetCode）

自底向上的层序遍历
思路：把上面一题的结果res数组反转一下就可以了，我们这里把当层的结果curLevel插入数组头部即可（上一题是push压入尾部）

/*
* @lc app=leetcode.cn id=107 lang=javascript
*
* [107] 二叉树的层序遍历 II
*/

// @lc code=start
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
*     this.val = (val===undefined ? 0 : val)
*     this.left = (left===undefined ? null : left)
*     this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrderBottom = function(root) {
   let res = [], queue = []
   // 第一排根先入队
   queue.push(root)
   if(root === null) return res

   while(queue.length != 0) {
       // 记录当层级节点数
       let len = queue.length
       // 存放每一层节点
       let curLevel = []
       for(let i = 0; i < len; i++) {
           // 弹出队里首位并且把当前节点的val压入到存放节点的数组
           let node = queue.shift()
           curLevel.push(node.val)
           // 当前层下一层的节点入队
           node.left && queue.push(node.left)
           node.right && queue.push(node.right)
       }
       // 从数组前头插入值，避免最后反转数组，减少运算时间
       res.unshift(curLevel);    
   }
   return res
};
// @lc code=end

199. 二叉树的右视图 - 力扣（LeetCode）

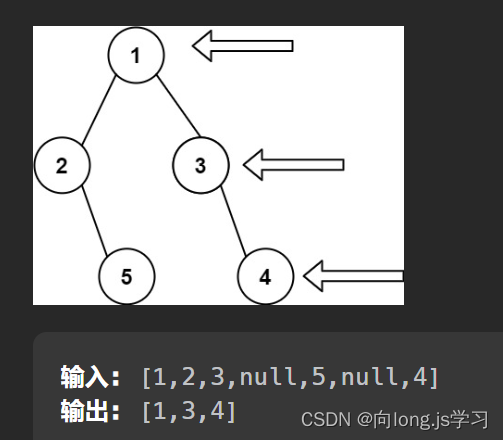
在这里插入图片描述

层序遍历的时候，判断是否遍历到单层的最后面的元素，如果是，就放进result数组中，随后返回result就可以了。

/*
 * @lc app=leetcode.cn id=199 lang=javascript
 *
 * [199] 二叉树的右视图
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var rightSideView = function(root) {
    //二叉树右视图 只需要把每一层最后一个节点存储到res数组
    let res = [], queue = [];
    queue.push(root);

    while(queue.length && root!==null) {
        // 记录当前层级节点个数
        let length = queue.length;
        while(length--) {
            let node = queue.shift();
            // length长度为0的时候表明到了层级最后一个节点
            if(!length) {
                res.push(node.val);
            }
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }

    return res;
};
// @lc code=end

429. N 叉树的层序遍历 - 力扣（LeetCode）

思路:
这道题依旧是模板题，只不过一个节点有多个孩子了

/*
 * @lc app=leetcode.cn id=429 lang=javascript
 *
 * [429] N 叉树的层序遍历
 */

// @lc code=start
/**
 * // Definition for a Node.
 * function Node(val,children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */

/**
 * @param {Node|null} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    //每一层可能有2个以上,所以不再使用node.left node.right
    let res = [], queue = [];
    queue.push(root);

    while(queue.length && root!==null) {
        //记录每一层节点个数还是和二叉树一致
        let length = queue.length;
        //存放每层节点 也和二叉树一致
        let curLevel = [];
        while(length--) {
            let node = queue.shift();
            curLevel.push(node.val);

            //这里不再是 ndoe.left node.right 而是循坏node.children
           for(let item of node.children){
               item && queue.push(item);
           }
        }
        res.push(curLevel);
    }

    return res;   
};
// @lc code=end

515. 在每个树行中找最大值 - 力扣（LeetCode）

思路：
层序遍历，取每一层的最大值

/*
 * @lc app=leetcode.cn id=515 lang=javascript
 *
 * [515] 在每个树行中找最大值
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var largestValues = function(root) {
    //使用层序遍历
    let res = [], queue = [];
    queue.push(root);

    while(root !== null && queue.length) {
        //设置max初始值就是队列的第一个元素
        let max = queue[0].val;
        let length = queue.length;
        while(length--) {
            let node = queue.shift();
            max = max > node.val ? max : node.val;
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        //把每一层的最大值放到res数组
        res.push(max);
    }

    return res;
};
// @lc code=end

104. 二叉树的最大深度 - 力扣（LeetCode）

思路：
使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。
在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：
[图片]

所以这道题的迭代法就是一道模板题，可以使用二叉树层序遍历的模板来解决的。

/*
 * @lc app=leetcode.cn id=104 lang=javascript
 *
 * [104] 二叉树的最大深度
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    // 最大的深度就是二叉树的层数
    if (root === null) return 0;
    let queue = [root];
    let height = 0;
    while (queue.length) {
        let n = queue.length;
        height++;
        for (let i=0; i<n; i++) {
            let node = queue.shift();
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
    }
    return height;
};
// @lc code=end

111. 二叉树的最小深度 - 力扣（LeetCode）

相对于 104.二叉树的最大深度，本题还也可以使用层序遍历的方式来解决，思路是一样的。
需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

/*
 * @lc app=leetcode.cn id=111 lang=javascript
 *
 * [111] 二叉树的最小深度
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function(root) {
    if (root === null) return 0;
    let queue = [root];
    let depth = 0;
    while (queue.length) {
        let n = queue.length;
        depth++;
        for (let i=0; i<n; i++) {
            let node = queue.shift();
            // 如果左右节点都是null(在遇见的第一个leaf节点上)，则该节点深度最小
            if (node.left === null && node.right === null) {
                return depth;
            }
            node.left && queue.push(node.left);;
            node.right && queue.push(node.right);
        }
    }
    return depth;
};
// @lc code=end

总结

二叉树的层序遍历，就是图论中的广度优先搜索在二叉树中的应用，需要借助队列来实现（此时又发现队列的一个应用了）。

扩展

在二叉树中，广度优先搜索的应用主要包括以下几个方面：

层次遍历：广度优先搜索可以实现对二叉树的层次遍历。从二叉树的根节点开始，先将根节点放入队列中，然后对队列中的节点进行出队操作，依次输出节点的值，并将其左右子节点放入队列中，直到队列为空。
查找最短路径：在二叉树中，广度优先搜索可以用于查找根节点到某个节点的最短路径。首先将根节点放入队列中，然后对队列中的节点进行出队操作，依次遍历节点的左右子节点，如果找到目标节点，则直接返回路径长度；否则，将子节点加入队列中，继续遍历，直到队列为空。
找到某一层节点：可以使用广度优先搜索来找到二叉树中的某一层节点。首先将根节点放入队列中，然后对队列中的节点进行出队操作，记录当前节点所在的层数，如果层数等于目标层，则将节点加入结果列表中；否则，将子节点加入队列中，继续遍历，直到队列为空。
判断是否为完全二叉树：广度优先搜索还可以用于判断二叉树是否为完全二叉树。首先将根节点放入队列中，然后对队列中的节点进行出队操作，依次遍历节点的左右子节点，如果当前节点只有右子节点没有左子节点，或者当前节点已经出现了只有左子节点没有右子节点的节点，则说明这不是一颗完全二叉树，直接返回false；否则，将子节点加入队列中，继续遍历，直到队列为空。如果成功遍历完所有节点，则说明这是一颗完全二叉树，返回true。

广度搜索