文章目录
- 1. 两数相加
- 2. K 个一组翻转链表
- 3. 合并 K 个升序链表
- 4. 路径总和I
- 5. 路径总和II
1. 两数相加
题目详情见: LeetCode2. 两数相加
题目描述相对来说比较绕, 我们可以直接理解为两个多位的整数相加, 只不过整数的每一位都是通过链表进行存储; 比如, 整数 342, 通过链表存储正常来说应该是 3->4->2, 但是计算时, 往往需要从低位开始计算, 逢十进一, 所以题目中直接将整数表示为 2->4->3, 这样反而不用将链表顺序进行反转了, 直接相加就可以了.
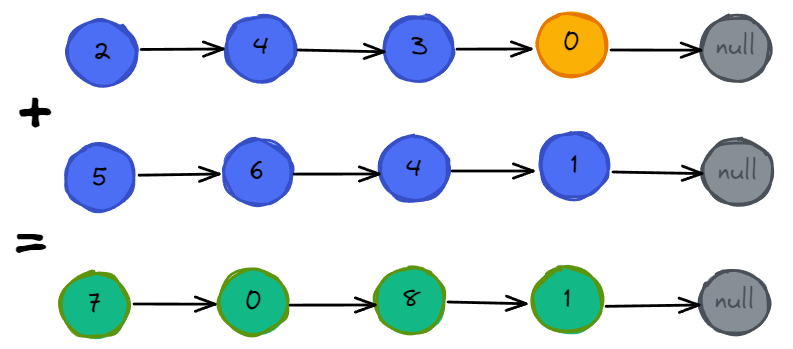
需要注意的是如果两个链表的长度不同, 则可以认为长度短的链表的后面有若干个 0, 链表遍历结束, 则如果进位值大于0, 则还需要在结果链表中附加一个值为1的节点.
因为链表是逆序的, 因此直接对应数字相加即可; 基本操作是遍历两个链表, 逐位计算它们的和, 并与当前位置的进位值相加.
比如, 两个链表对应位的数字分别为 n1 和 n2, 进位为 carry (初始值为0, 有 0 和 1 两种取值), 则它们的和为 n1 + n2 + carry, 对应位上数字变为 (n1 + n2 + carry) % 10, 新的进位为(n1 + n2 + carry) / 10.
如果两个链表长度不一样, 长度短的链表后续对应位上值均为0即可; 如果遍历结束之后, carray大于0 (也就是等于1), 则在结构链表后面新增一个节点.
代码实现如下:
class Solution {
// 计算链表长度
public static int listLength(ListNode head) {
int len = 0;
while (head != null) {
len++;
head = head.next;
}
return len;
}
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode cur1 = l1;
ListNode cur2 = l2;
// 让cur1指向较长的链表
int len1 = listLength(cur1);
int len2 = listLength(cur2);
if (len1 < len2) {
cur1 = l2;
cur2 = l1;
}
ListNode retHead = cur1;
int carry = 0; // 记录进位
int curNum = 0;
// 记录长链表遍历到哪里了
// 方便遍历完两个链表之后如果还有进位, 就new一个新的节点方便尾插到链表中.
ListNode last = cur1;
// 首先遍历至较短链表为null
while (cur2 != null) {
curNum = cur1.val + cur2.val + carry;
cur1.val = curNum % 10;
carry = curNum / 10;
last = cur1;
cur1 = cur1.next;
cur2 = cur2.next;
}
// 继续接着上面的位置遍历长链表
while (cur1 != null) {
curNum = cur1.val + carry;
cur1.val = curNum % 10;
carry = curNum / 10;
last = cur1;
cur1 = cur1.next;
}
if (carry != 0) {
last.next = new ListNode(1);
}
return retHead;
}
}
2. K 个一组翻转链表
题目详情见: LeetCode25. K 个一组翻转链表
本题需要设计两个方法:
第一个方法ListNode getKGroupEnd(ListNode startNode, int k): 从链表 startNode 位置开始是第 1 个节点, 数够 k 个节点,返回第 k 个节点.
比如链表为:
...-> startNode -> b -> c -> d -> e
k = 3
表示从 start 开始, 数够 3 个, 所以返回 c 节点
如果是下述情况
...-> start -> b -> c -> null
k = 6
由于 start 后面不够 6 个, 所以返回 null.
// 找到每组内要逆序的尾节点返回
private static ListNode getKGroupEnd(ListNode startNode, int k) {
while (--k != 0 && startNode != null) {
startNode = startNode.next;
}
return startNode;
}
第二个方法void reverse(ListNode startNode, ListNode endNode), 表示反转 startNode 到 endNode 之间的链表.
例如: 原链表为
....->a->b->c->d->e....
假设 startNode = a, endNode = d, 经过reverse方法, 会变成
...d->c->b->a->e.....
reverse 方法也相对比较简单, 实现代码如下:
public static void reverse(ListNode start, ListNode end) {
end = end.next;
ListNode pre = null;
ListNode cur = start;
while (cur != end) {
ListNode tmp = cur.next;
cur.next = pre;
pre = cur;
cur = tmp;
}
start.next = end;
}
有了上述两个方法, 我们可以比较方便实现原题要求, 主流程如下:
- 首先要先将第一组进行反转.
- 每次的反转如果节点个数小于 k 了, 就直接返回.
- 每次组内反转之后的组内尾节点就是 startNode 了, 用 lastEndNode 记录下来.
- 每次反转之后要记得和前一个组的尾节点连接, 即和 lastEndNode 连接.
- 只要 lastEndNode 的下一个节点不为 null, 就还可以继续分组反转.
完整代码如下:
class Solution {
// 找到每组内要逆序的尾节点返回
private static ListNode getKGroupEnd(ListNode startNode, int k) {
while (--k != 0 && startNode != null) {
startNode = startNode.next;
}
return startNode;
}
private static void reverse(ListNode startNode, ListNode endNode) {
endNode = endNode.next;
ListNode cur = startNode;
ListNode prev = null;
ListNode curNext = null;
while (cur != endNode) {
curNext = cur.next;
cur.next = prev;
prev = cur;
cur = curNext;
}
startNode.next = endNode;
}
public ListNode reverseKGroup(ListNode head, int k) {
ListNode startNode = head;
// 先将第一组进行反转
ListNode endNode = getKGroupEnd(startNode, k);
// 链表中节点个数小于k, 直接返回
if (endNode == null) {
return head;
}
// 第一次进行反转后的endNode节点就是最终要返回的头节点了
head = endNode;
// 反转
reverse(startNode, endNode);
// 拿到第一组反转后的组内尾节点
ListNode lastEndNode = startNode;
while (lastEndNode.next != null) {
startNode = lastEndNode.next;
endNode = getKGroupEnd(startNode, k);
if (endNode == null) {
return head;
}
reverse(startNode, endNode);
// 与前面的内容进行连接
lastEndNode.next = endNode;
lastEndNode = startNode;
}
return head;
}
}
3. 合并 K 个升序链表
题目详情见: LeetCode23. 合并 K 个升序链表
思路如下:
准备一个小根堆, 并把每个链表的头节点加入到小根堆中, 此时, 小根堆堆顶弹出的节点一定是最后生成新链表的头节点.
假设链表为: L1,L2…LN
- 第一步, 先将 L1,L2…LN 的头节点 L1H,L2H…LNH 加入小根堆;
- 第二步, 从小根堆堆顶弹出一个元素, 作为最后链表的头节点;
- 第三步, 第二步中弹出节点所在的链表, 假设是 i 号链表, 那么就找弹出节点的下一个节点 (不为 null) 再入堆;
- 第四步, 循环, 只要堆不为空就弹出堆顶节点添加到新链表中, 只要堆顶节点的下一个节点不为 null 就将这个节点再入堆.
这样就能保证每次添加的新链表节点是所有链表节点中最小的那一个.
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists == null) {
return null;
}
PriorityQueue<ListNode> heap = new PriorityQueue<ListNode>(new Comparator<ListNode>() {
@Override
public int compare(ListNode o1, ListNode o2) {
return o1.val - o2.val;
}
});
for (int i = 0; i < lists.length; i++) {
if (lists[i] != null) {
heap.offer(lists[i]);
}
}
if (heap.isEmpty()) {
return null;
}
ListNode head = heap.poll();
ListNode tail = head;
if (tail.next != null) {
heap.offer(tail.next);
}
while (!heap.isEmpty()) {
ListNode cur = heap.poll();
tail.next = cur;
tail = cur;
if (cur.next != null) {
heap.offer(cur.next);
}
}
return head;
}
}
4. 路径总和I
题目详情见: 112. 路径总和
使用递归, 先从根结点搜索一条路径到底, 不符合条件后便后退一步, 然后继续进行搜索.
class Solution112 {
/*// 方法一
// 一直想向下递归, 每次sum减去当前节点的值
// 碰到叶子节点后判断叶子节点中的值和剩下的值是否相同
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
return process(root, targetSum);
}
public static boolean process(TreeNode childRoot, int subSum) {
if (childRoot.left == null && childRoot.right == null) {
return childRoot.val == subSum;
}
boolean ans = childRoot.left != null ? process(childRoot.left, subSum - childRoot.val) : false;
ans |= childRoot.right != null ? process(childRoot.right, subSum - childRoot.val) : false;
return ans;
}*/
// 方法二
// 向下递归的过程累加节点值
// 到叶子节点后判断和目标值是否相同
public static boolean isSum;
public static boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
isSum = false;
process(root, 0, targetSum);
return isSum;
}
public static void process(TreeNode childRoot, int preSum, int sum) {
if (childRoot.left == null && childRoot.right == null) {
if (childRoot.val + preSum == sum) {
isSum = true;
}
return ;
}
// childRoot是非叶子节点
preSum += childRoot.val;
if (childRoot.left != null) {
process(childRoot.left, preSum, sum);
}
if (childRoot.right != null) {
process(childRoot.right, preSum, sum);
}
}
}
5. 路径总和II
题目详情见: 113. 路径总和 II
与上一题不同, 这个题需要我们找出所有路径之和等于目标值的具体路径; 所以我们在搜索的过程中需要使用一个顺序表来记录当前的路径, 当该条路径符合题意时将其存入最后返回的顺序表中即可; 这个题特别需要注意的是搜索路径在回退时一定要注意将当前节点从路径中删除.
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> ans = new ArrayList<>();
if (root == null) {
return ans;
}
ArrayList<Integer> path = new ArrayList<>();
process(root, path, 0, targetSum, ans);
return ans;
}
public static void process(TreeNode root, List<Integer> path, int preSum,
int sum, List<List<Integer>> ans) {
// 叶子节点
if (root.left == null && root.right == null) {
if (preSum + root.val == sum) {
path.add(root.val);
ans.add(new ArrayList<>(path));
// 将当前节点从路径中删除
path.remove(path.size() - 1);
}
return;
}
// 非叶子节点
path.add(root.val);
preSum += root.val;
if (root.left != null) {
process(root.left, path, preSum, sum, ans);
}
if (root.right != null) {
process(root.right, path, preSum, sum, ans);
}
path.remove(path.size() - 1);
}
}