6-2 装载问题（分支限界）

一、问题描述

有一批共个集装箱要装上2艘载重量分别为C1和C2的轮船，其中集装箱i的重量为Wi，且

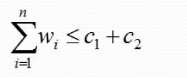
采用下面的策略可得到最优装载方案：
(1)将第一艘轮船尽可能装满;
(2)将剩余集装箱装上第二艘轮船;

二、问题分析

1、队列式分支限界法

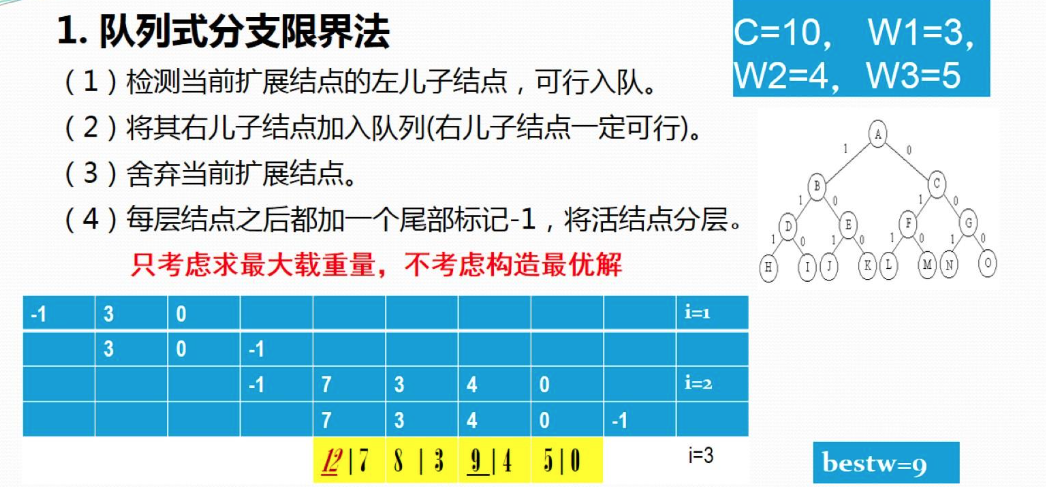
⒉.算法的改进(右子树加入剪枝条件)
上述算法中右子没有剪枝，效率较差。
策略:设bestw是当前最优解;ew是当前扩展结点所相应的重量;r是剩余集装箱的重量。
则当ew+rsbestw时，可将其右子树剪去。
为确保右子树成功剪枝，算法每一次进入左子树的时候更新bestw的值。不要等待i=n时才去更新。

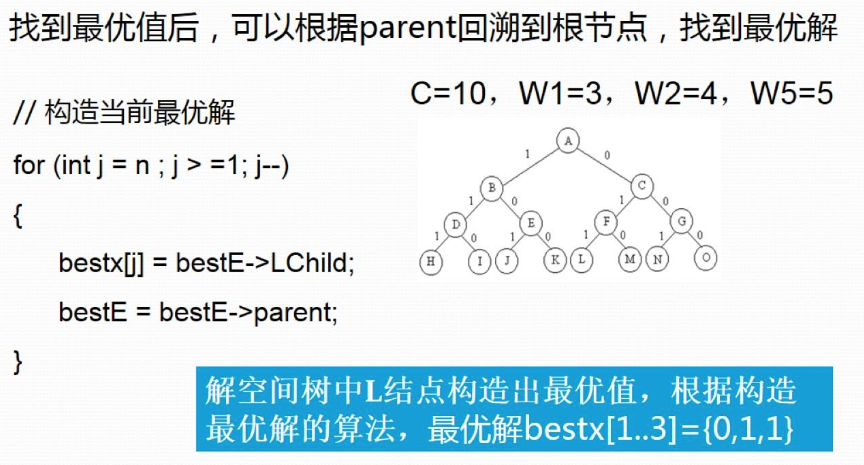
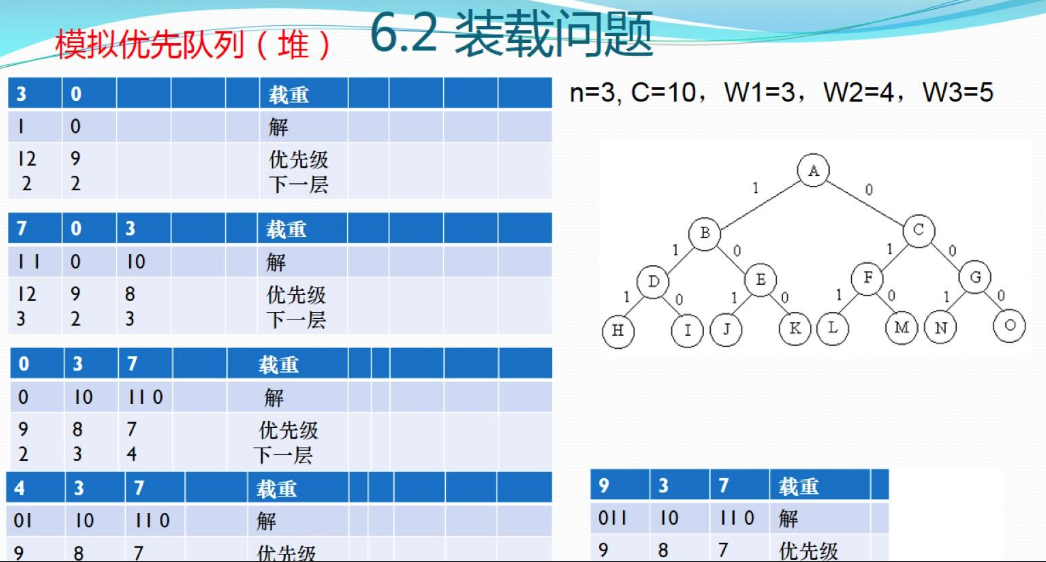
三、代码

//队列式分支限界法  
/*没有构造最优解
10 3
3 4 5

10 4
3  4 5 6
*/
#include<iostream> 
#include<queue> 
using namespace std;
queue<int>q;
int w[100]; //集装箱的重量 
int c;
int r;//r剩余没装的总重量 ，r的初值为全部集装箱重量之和 
int n;//n个集装箱 
int bestw=0;//当前最优载重量 
void MaxLoading(){
	int top=0;
	int left=r;
	q.push(-1);
	int i=1;//第i层 
	r=r-w[1];
	while(i<=n&& !q.empty()){
		if(i==1){
			if(top+w[i]<=c){
				q.push(top+w[i]);	
				cout<<top+w[i]<<" ";
			}
			q.push(top); 
			cout<<top<<" ";
		}
		top=q.front();
		q.pop();
		if(top==-1&&!q.empty()){
			q.push(-1);
			cout<<"-1\n";
			i++;
			top=q.front();
			q.pop();
			r=r-w[i];
		}
		int wt=top+w[i];
		if(wt<=c){
			if(wt>bestw) bestw=wt;
			if(i<n){
				q.push(wt);
				cout<<wt<<" ";
			} 
		}
		if(top+r>bestw){
			if(i<n){
				q.push(top);
				cout<<top<<" ";
			} 
		}
	}
		
} 
int main(){
	cin>>c;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>w[i];	
		r=r+w[i];
	}	
	cout<<"----------\n";
	MaxLoading();
	cout<<"bestw="<<bestw<<endl; 
	return 0;
}