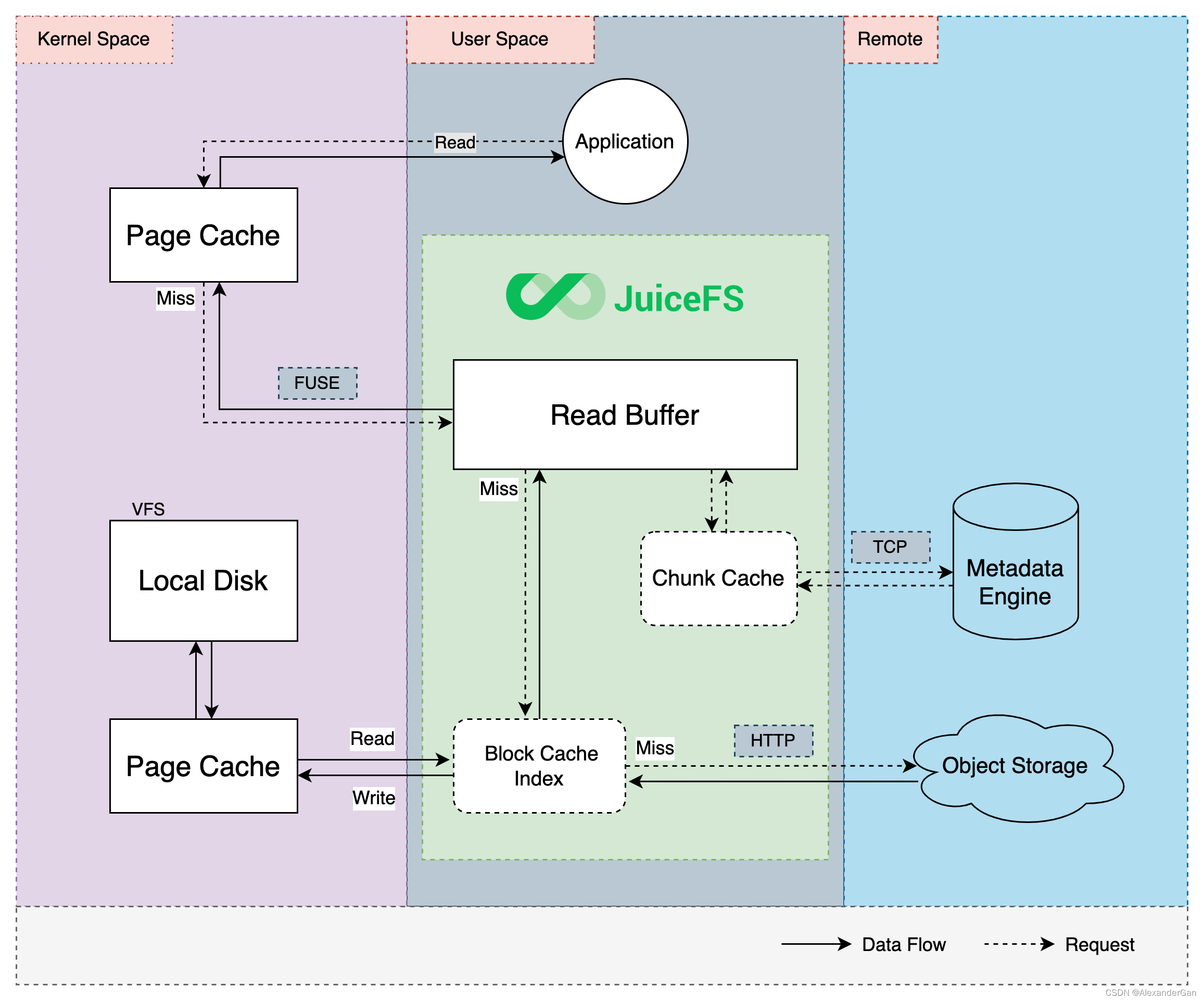
阶码和尾数
- 阶码
- 尾数
- 浮点数
- 浮点数表示
- 示例
- 例题分析
- 总结
阶码
在机器中表示一个浮点数时需要给出指数,这个指数用整数形式表示,这个整数叫做阶码。
尾数
常用对数的小数部分,用于科学计数法,其表示方法为:Mantissa x Base^Exponent(尾数x 基数^指数)
浮点数
一个实数由一个整数或定点数(即尾数)乘以某个基数(计算机中通常是2)的整数次幂得到,这种表示方法类似于基数为10的科学计数法
浮点数表示
N=Mx Re
M是尾数
e是指数
R为基数
示例
一个十进制数写成一个纯小数乘上10的若干次方
1024=1.024×103
一个二进制数也可写成一个纯小数乘上2的若干次方。
11.01=0.1101×22
任一个二进制N,可表示为N=2e×M;
其中e为二进制数,叫阶码;
e如果有正负号的话,正负号就叫阶符;
M为纯小数,叫做尾数;
数符,指的是N(整个数)的符号。
浮点数能表示的范围由阶码的位数决定,精确度有尾数的位数决定
例题分析

由给出的数可知前五位10001为1位的阶符和4位阶码组成
阶符1代表是负数
0001是阶码的补码,可知阶码的原码为1111,转化成10进制是15。阶码就是-15
这里增加
原码转换为补码的规则:符号位不变,数值位按位取反,末位再加1

数符为第6位,此处是0,代表整个数是正数。
尾数是后10位,用原码表示0000 000001,这个数是多少呢?
先看一个例子:
110.11这个数转化成10进制数是多少
110.11=1x 22+1x 21+0x 20+1x 2-1+1x 2-2
0乘以任何数都等于0,1乘以任何数都等于任何数,所以上面的例子可以直接简化为
110.11=22+ 21+ 2-1+2-2
大家是否看出规律了,小数点后面的数的指数是从-1开始,1位就是-1次方,2位就是-2次方,题目中0000 000001,是第10位为1,所以是2-10
至此,这个题结合前面提到的N=2e×M,把尾数和阶码合在一起写的结果就是
2-15x 2^-10
总结
阶码和尾数不难理解,只要套用我们所熟知的十进制数,将基数变为2即可,同时也要对进制之间的转换和补码原码知识所熟悉。
·