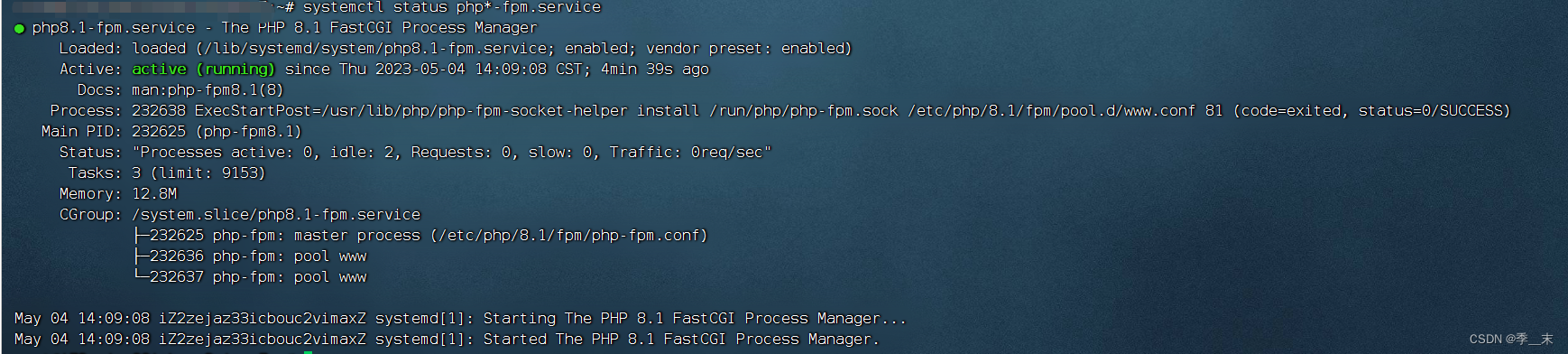
前言：

上一篇文章，我们已经讲完了冒泡排序，选择排序，插入排序和希尔排序。

那么我们今天来讲一下堆排序，快速排序和归并排序吧~

堆排序（Heap Sort）

堆排序是一种基于完全二叉树的排序算法。堆排序的基本思想是先将待排序的数据构建成一个大根堆或小根堆，然后将堆顶元素与堆底元素交换位置，然后将堆的大小减一，再调整堆使其重新成为一个大根堆或小根堆，重复上述步骤直到堆的大小为1为止。

构建大根堆或小根堆的过程可以通过自下而上或自上而下两种方式进行。自下而上的方式，从最后一个非叶子节点开始，依次将每个节点作为根节点进行调整，使其成为一个子树的大根堆或小根堆。自上而下的方式，则是从根节点开始，依次将左右子树调整为大根堆或小根堆，然后再将整个树调整为一个大根堆或小根堆。

堆排序的优点是不需要额外的辅助空间，而且可以在最坏情况下保证 O(nlogn) 的时间复杂度。缺点是不稳定，无法保证相同元素的相对位置不变。

来看下面的动图：

看完动图之后，直接来看代码吧~

void heap_sort(int arr[], int n);
void heapify(int arr[], int n, int i);

void heap_sort(int arr[], int n) {
    // 构建大根堆
    for (int i = n / 2 - 1; i >= 0; i--)
        heapify(arr, n, i);
    
    // 进行堆排序
    for (int i = n - 1; i > 0; i--) {
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;
        heapify(arr, i, 0);
    }
}

void heapify(int arr[], int n, int i) {
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    
    if (left < n && arr[left] > arr[largest])
        largest = left;
    
    if (right < n && arr[right] > arr[largest])
        largest = right;
    
    if (largest != i) {
        int temp = arr[i];
        arr[i] = arr[largest];
        arr[largest] = temp;
        heapify(arr, n, largest);
    }
}

 堆的数据结构和性质是堆排序的灵魂，是堆排序能够高效实现的关键。

快速排序（Quick Sort）（递归实现）

快速排序是常用的一种基于分治思想的排序算法。

快速排序的基本思想是选定一个基准元素（pivot），将待排序的数据分为两个子序列，其中一个子序列中的所有元素都比基准元素小，另一个子序列中的所有元素都比基准元素大。然后分别对这两个子序列递归地进行快速排序，最终将整个序列排序。

快速排序的关键在于如何选取基准元素。一般来说，可以选择序列的第一个元素、最后一个元素、中间元素或随机元素作为基准元素。

快速排序也有三种版本，分别为hoare版本，挖坑法，前后指针法

那么我们先来看hoare

hoare

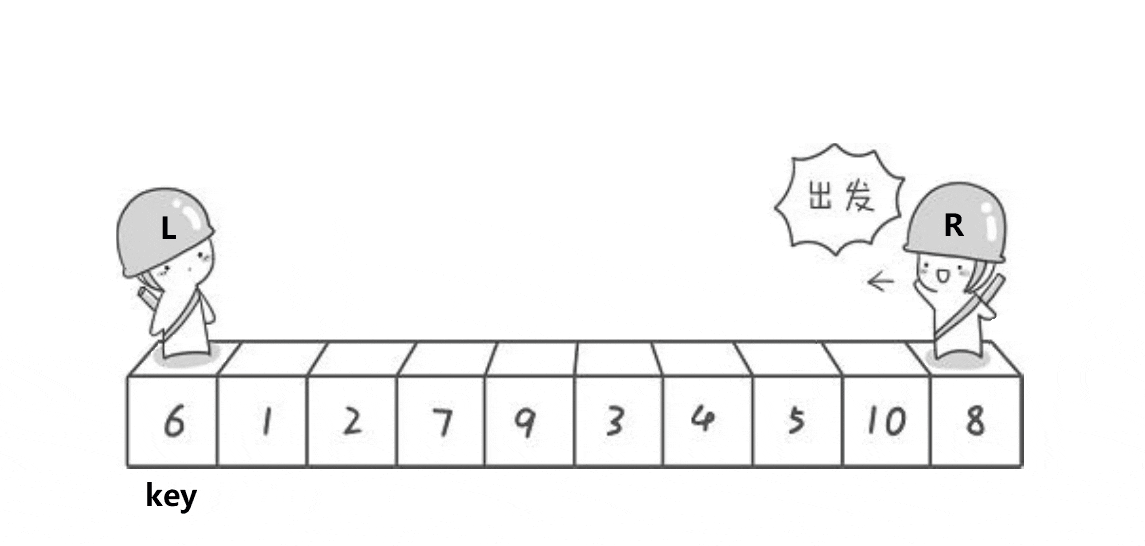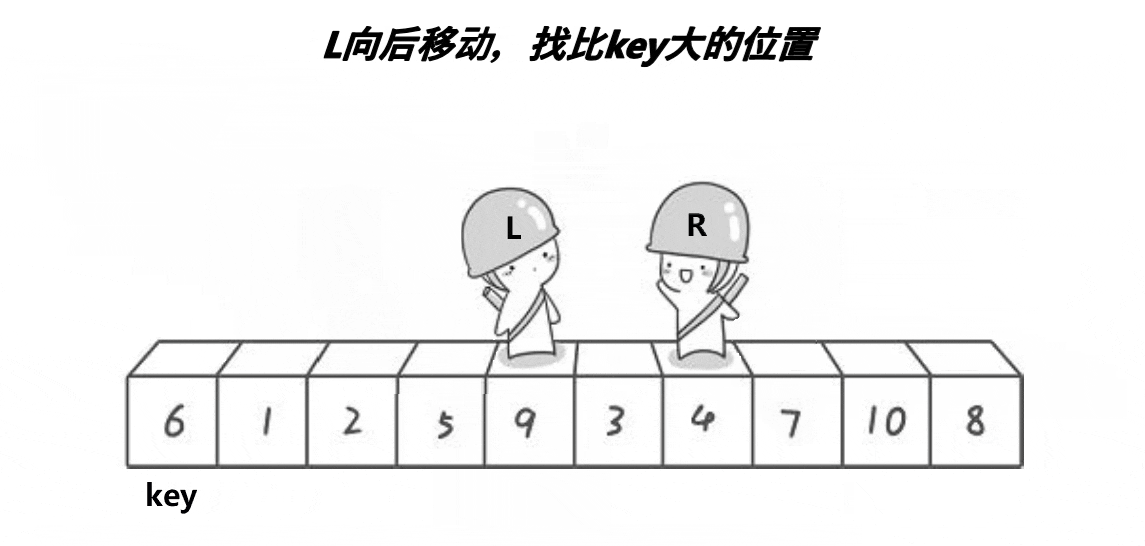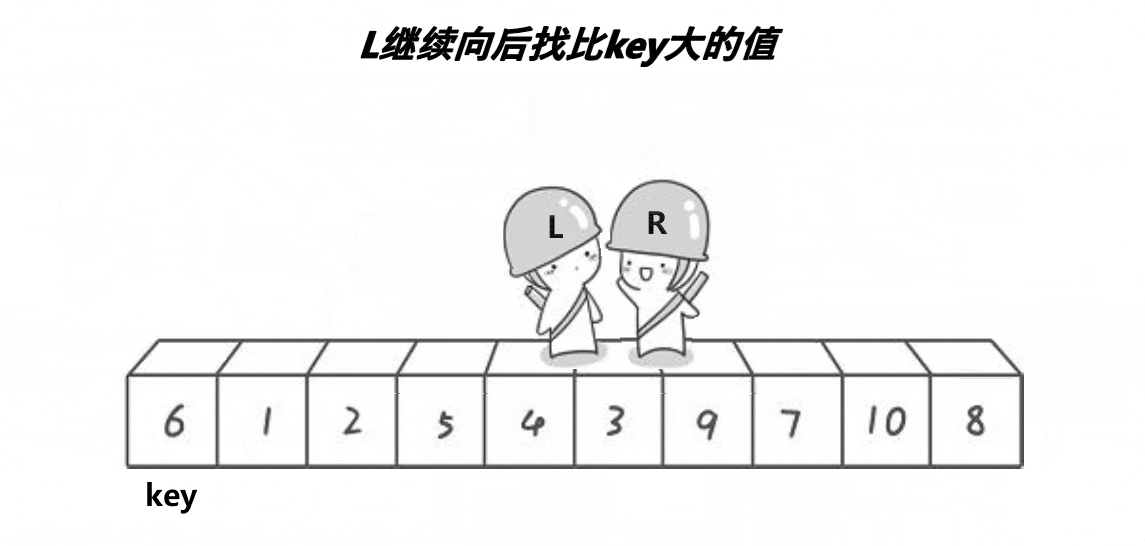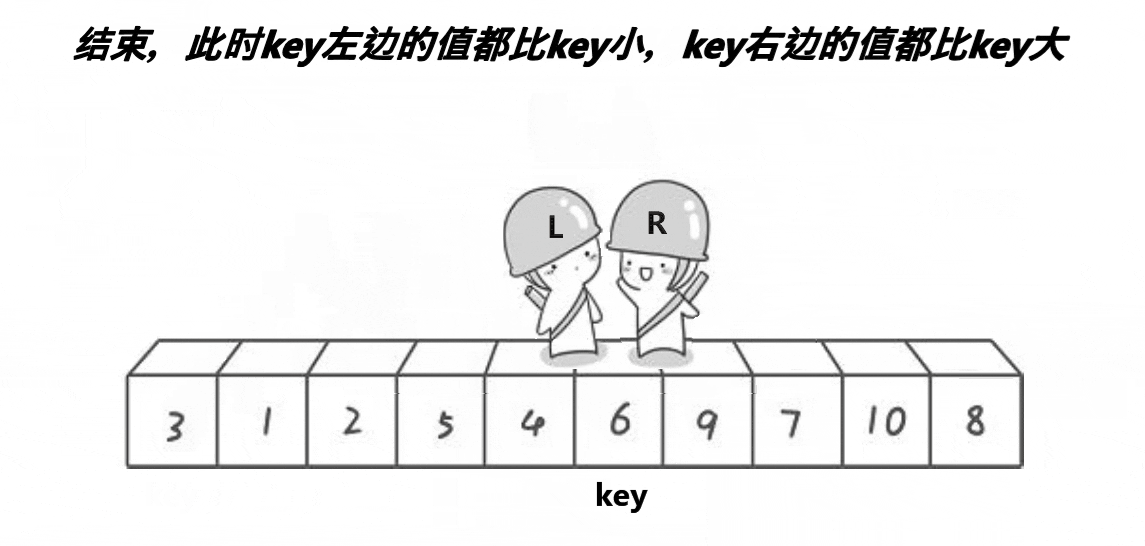
看到上面的动图了吗？

我们一开始把左边小人站的位置的值当作基准值，我们的右边小人就会开始往左走，直到找到了比我们基准值还要小的数停下，之后我们的左边小人才会开始向右走，直到找到一个比基准值还要大的值，之后两个小人所站的两个值互换即可，依次进行下去，两个小人就会在某个地方会合，那么我们会把基准值和两个小人会合的值互换位置，这就完成了一次快速排序，之后将这次基准值的左右侧分别进行快速排序进行递归就可以完成这整一套的快速排序啦

那么我们就看代码吧~

void QuickSort1(int* a, int left, int right)
{
	if (left >= right)
		return;

	int begin = left, end = right;

	 随机选key
	/*int randi = left + (rand() % (right - left));
	Swap(&a[left], &a[randi]);*/

	// 三数取中
	int midi = GetMidNumi(a, left, right);
	if(midi != left)
		Swap(&a[midi], &a[left]);

	int keyi = left;
	while (left < right)
	{
		// 右边找小
		while (left < right && a[right] >= a[keyi])
			--right;

		// 左边找大
		while (left < right && a[left] <= a[keyi])
			++left;

		Swap(&a[left], &a[right]);
	}

	Swap(&a[keyi], &a[left]);
	keyi = left;

	// [begin, keyi-1] keyi [keyi+1, end] 
	// 递归
	QuickSort1(a, begin, keyi - 1);
	QuickSort1(a, keyi+1, end);
}

 我们的递归结束条件就是区间的left>=right。

挖坑法

挖坑法快速排序是快速排序的一种变体，相比于传统的交换元素法，它的优势在于减少了交换操作的次数，从而提高了排序的效率。

在传统的快速排序中，每当找到一个需要交换的元素时，需要进行一次交换操作。而在挖坑法快速排序中，只需要将需要交换的元素的值拷贝到一个临时变量中，然后用这个值去填补基准元素的坑位，从而达到交换元素的目的。这样，就避免了不必要的交换操作，提高了排序的效率。

当然，除了提高了排序的效率，我认为，挖坑法比传统的Hoare更好理解。

那么老样子，还是先来看动图吧~

看完了动图，我们马上就可以写出它的代码

void QuickSort2(int* a, int left, int right)
{
	if (left >= right)
		return;

	int begin = left, end = right;

	// 三数取中
	int midi = GetMidNumi(a, left, right);
	if (midi != left)
		Swap(&a[midi], &a[left]);

	
	int key = a[left];
	int hole = left;
	while (left < right)
	{
		// 右边找小
		while (left < right && a[right] >= key)
			--right;

		a[hole] = a[right];
		hole = right;

		// 左边找大
		while (left < right && a[left] <= key)
			++left;

		a[hole] = a[left];
		hole = left;
	}

	a[hole] = key;

	// [begin, hole-1] hole [hole+1, end] 
	// 递归
	QuickSort2(a, begin, hole - 1);
	QuickSort2(a, hole + 1, end);
}

前后指针法

前后指针法是快速排序的一种常用实现方式，其基本思想是通过两个指针从序列的两端开始向中间移动，找到需要交换的元素并进行交换，最终完成排序。

cur一直向前遍历，只有cur位置上的值比基准值小时，prev向前遍历。当cur和prev之间有差距，说明两者之间都为比基准值大的元素，交换cur和prev上的元素。最后将基准值和prev最后停下来位置上的元素进行交换。

来看动图

看完动图就来写代码吧~ 

void quickSort3(int arr[], int left, int right) {
    int i, j, pivot, temp;
    if (left < right) {
        pivot = arr[left];
        i = left;
        j = right;
        while (i < j) {
            while (i < j && arr[j] > pivot)
                j--;
            while (i < j && arr[i] <= pivot)
                i++;
            if (i < j) {
                temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
        arr[left] = arr[i];
        arr[i] = pivot;
        quickSort3(arr, left, i - 1);
        quickSort3(arr, i + 1, right);
    }
}

以上均为递归实现的快速排序~

那么我们还要来学习非递归的快速排序

快速排序（非递归）

有人可能会问了，正常情况下怎么样才能实现递归呢？

其实仔细看这个快速排序，如果两边分配的均匀的话，是不是排序有点像分解一棵二叉树？

我们就需要通过一个介质来保存每一层递归的信息，比如左右边界，还有递归的深度，那么模拟实现非递归的介质就是------栈~

void quickSort(int arr[], int left, int right) {
    int stack[128];
    int top = -1;
    stack[++top] = left;
    stack[++top] = right;
    while (top >= 0) {
        right = stack[top--];
        left = stack[top--];
        int i = left;
        int j = right;
        int pivot = arr[left];
        while (i < j) {
            while (i < j && arr[j] >= pivot)
                j--;
            if (i < j)
                arr[i++] = arr[j];
            while (i < j && arr[i] <= pivot)
                i++;
            if (i < j)
                arr[j--] = arr[i];
        }
        arr[i] = pivot;
        if (left < i - 1) {
            stack[++top] = left;
            stack[++top] = i - 1;
        }
        if (i + 1 < right) {
            stack[++top] = i + 1;
            stack[++top] = right;
        }
    }
}

int main() {
    int arr[] = {5, 2, 6, 3, 1, 4};
    int n = sizeof(arr) / sizeof(arr[0]);
    quickSort(arr, 0, n - 1);
    for (int i = 0; i < n; i++)
        printf("%d ", arr[i]);
    printf("\n");
    return 0;
}

也许有同学发现了上面的一些特殊代码，例如：三数取中。

这就要谈谈实际出现的特殊情况了，如果一开始我们的序列就是有序的或者是基本有序的，然后我们又选出的是序列的开头的值为基准值，这个基准值很有可能是整个序列的最大值或最小值，我们所说的形似二叉树的样子就不太像了，他会分出两个子序列，一个子序列会特别的短，一个子序列会特别的长，那么我们递归排序要处理的数据就会十分的庞大，也就是说我们的快速排序的时间复杂度也会随之变大，变成了O（N^2），那么为了解决这个问题，我们有三种优化策略。

分别为：三路归并优化，三数取中优化，还有随机抽取基准值优化

三路归并

在普通的快速排序中，将序列分为小于和大于基准元素的两部分，而在三路归并优化中，将序列分为小于、等于和大于基准元素三部分，可以有效地处理重复元素。具体来说，将序列分成三部分后，对小于、等于和大于基准元素的部分分别进行递归排序，最后将三部分合并成一个有序序列

三数取中

在选择基准元素时，如果每次都选择序列的第一个或最后一个元素，可能会导致快速排序的时间复杂度退化为O(n^2)，因为如果序列本身已经有序或基本有序，每次选择的基准元素都是最大或最小值，这样分割出来的两部分序列大小差别很大，递归排序时需要处理的数据量也很大。为了避免这种情况，可以采用三数取中优化，即从序列的第一个、中间和最后一个元素中选择中间大小的元素作为基准元素，这样可以尽量保证分割出来的两部分序列大小相近，从而减少递归排序时需要处理的数据量，提高快速排序的效率。

随机抽取基准值

在选择基准元素时，也可以采用随机抽取基准值的方式，即从待排序序列中随机抽取一个元素作为基准元素，这样可以避免序列已经有序或基本有序的情况，从而提高快速排序的效率。此外，随机抽取基准值的方式也可以降低快速排序被恶意攻击的风险，比如有人故意构造一个特殊的序列，使得快速排序的时间复杂度退化到O(n^2)，从而导致程序崩溃或性能下降。

归并排序（Merge Sort）（递归）

归并排序是一种基于分治思想的排序算法，其基本思想是将待排序序列分成若干个子序列，对每个子序列进行排序，然后将子序列合并成一个有序序列。将子序列合并的过程中，需要使用额外的空间来存储合并后的序列，因此归并排序的空间复杂度较高。

具体来说，归并排序可以使用递归或非递归的方式实现。在递归实现中，将待排序序列不断分成左右两个子序列，对左右两个子序列分别进行递归排序，最后将两个有序子序列合并成一个有序序列。在非递归实现中，使用循环迭代的方式对子序列进行归并排序，最终得到有序序列。

 

// 合并两个有序序列
void merge(int arr[], int left, int mid, int right, int *temp) {
    int i = left;
    int j = mid + 1;
    int k = 0;
    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j])
            temp[k++] = arr[i++];
        else
            temp[k++] = arr[j++];
    }
    while (i <= mid)
        temp[k++] = arr[i++];
    while (j <= right)
        temp[k++] = arr[j++];
    for (i = 0; i < k; i++)
        arr[left + i] = temp[i];
}

// 归并排序
void mergeSort(int arr[], int left, int right, int *temp) {
    if (left < right) {
        int mid = (left + right) / 2;
        mergeSort(arr, left, mid, temp);
        mergeSort(arr, mid + 1, right, temp);
        merge(arr, left, mid, right, temp);
    }
}

一直一分为二，直到出现一个或零个时，递归结束，开始往回返，开始合并成一个有序的子序列。之后每一个子序列一直合并就会合成一个有序的序列了。.

那么我们可以用非递归实现吗？

当然是可以的，那我们还需要借助栈来实现吗？

答案是不用！

我们直接通过迭代就可以实现非递归的归并排序

// 归并排序的非递归实现
void mergeSort(int arr[], int n) {
    int *temp = (int *) malloc(n * sizeof(int));
    for (int step = 1; step < n; step *= 2) {
        for (int i = 0; i < n - step; i += 2 * step) {
            int left = i;
            int mid = i + step - 1;
            int right = i + 2 * step - 1 < n ? i + 2 * step - 1 : n - 1;
            int i1 = left, i2 = mid + 1, k = 0;
            while (i1 <= mid && i2 <= right) {
                if (arr[i1] <= arr[i2])
                    temp[k++] = arr[i1++];
                else
                    temp[k++] = arr[i2++];
            }
            while (i1 <= mid)
                temp[k++] = arr[i1++];
            while (i2 <= right)
                temp[k++] = arr[i2++];
            for (int j = 0; j < k; j++)
                arr[left + j] = temp[j];
        }
    }
    free(temp);
}