---

前言

完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

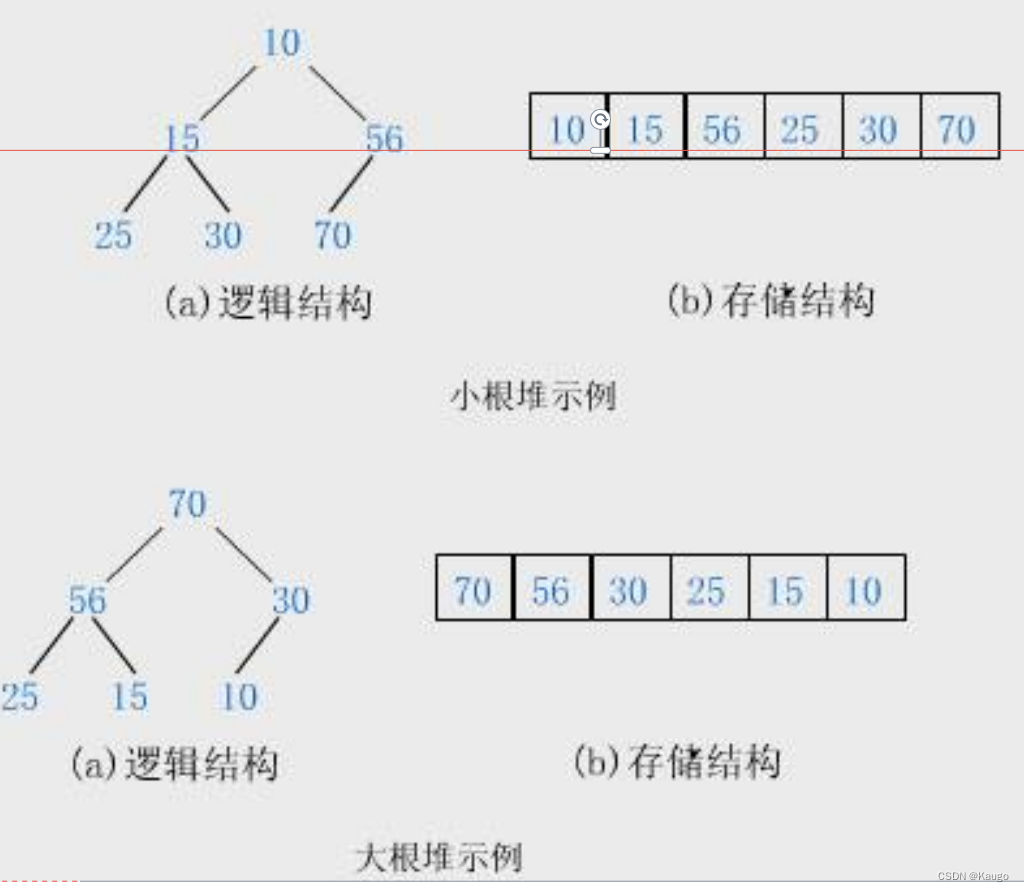
堆的性质：
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

---

一、堆的基本变量

typedef int HPDataType;//堆的数据类型
typedef struct Heap {
	HPDataType* a;//堆所指向空间地址
	int size;//当前容量
	int capacity;//最大容积
}HP;//结构体用来存放堆与堆的一些基本变量

二、堆的基本操作

2.1堆的初始化（HeapInit）

void HeapInit(HP* php) {
	assert(php);
	//堆是可以为空的，但是php是结构体
	//里面除了含有堆还有堆的基本量，
	//基本量不能为NULL
	//当堆为空，php不能为空，因为php-》size=0为有效值
	//所以需要断言php是否为空
	php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);
	//申请四个大小
	if (php->a == NULL) {
		perror("malloc");
		return;
	}//判断申请的空间是否为空
	php->size = 0;//初始大小为0
	php->capacity = 4;//最大容量为4
}

2.2堆的销毁（HeapDestroy）

void HeapDestroy(HP* php) {
	assert(php);
	free(php->a);
	//释放堆的空间
	php->a = NULL;
	php->capacity = php->size = 0;
	//容量与大小变为0
}

2.3向上调整（AdjustUp）

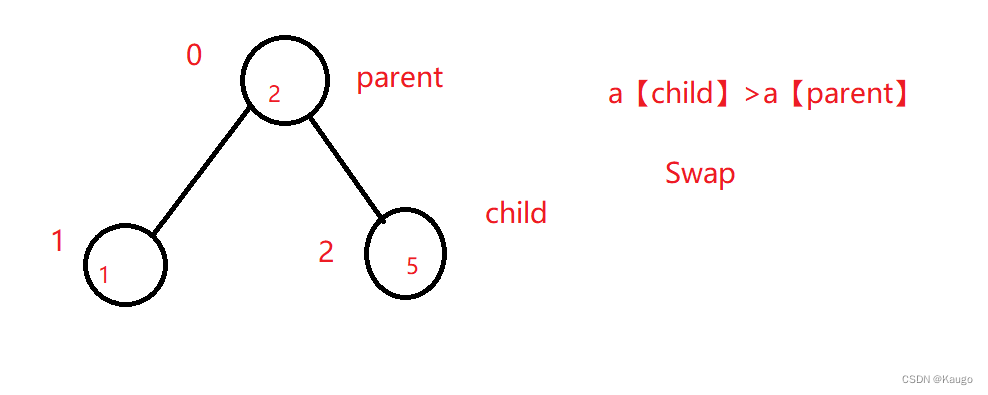
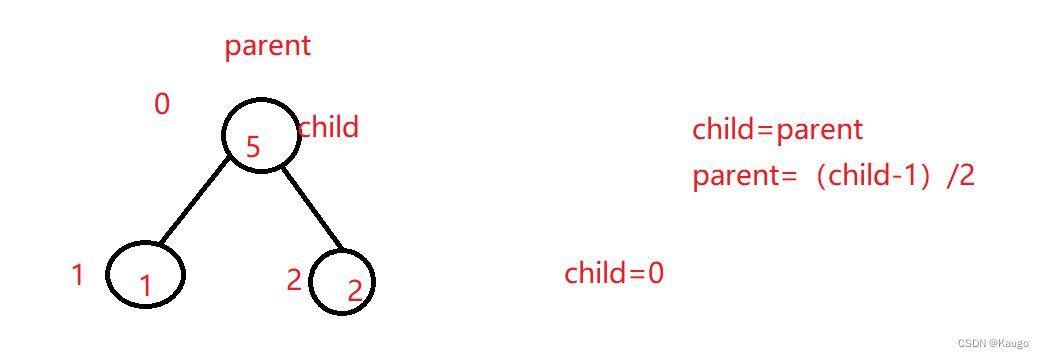
void AdjustUp(HPDataType* a, int child) {//这里我们以建大堆为例
	//向上调整条件：
	// 除了child这个位置前面的数据构成堆
	
	//大堆要父母比孩子大
	int parent = (child - 1) / 2;
	//父母的下标
	while (child > 0) {
		if (a[child] > a[parent]) {
			//孩子比父母大交换
			Swap(&a[child], &a[parent]);
			child = parent;
			//接着向上
			parent = (child - 1) / 2;
		}
		else{
			break;
		}
	}
}

2.4向下调整（AdjustDown）

图中是在建小堆，但我们代码以大堆为例，除了大于小于的方向不同，但逻辑是一样的

void AdjustDown(HPDataType* a, int n, int parent) {//以建大堆为例
	//向下调整条件：
	// 左右子树都是大堆/小堆

	int child = parent * 2 + 1;
	//孩子下标
	while ( child < n) {
		if (child + 1 < n && a[child + 1] > a[child]) {
			child++;//选出两个孩子中最大的那一个
		}
		if (a[child] > a[parent]) {
			//最大的那一个去与父母比较
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else{
			break;
		}
	}
}

2.45堆是否为空（HeapEmpty）

bool HeapEmpty(HP* php) {
	assert(php);
	return php->size == 0;
	//为0返回true否则返回false
}

2.5堆的插入（HeapPush）

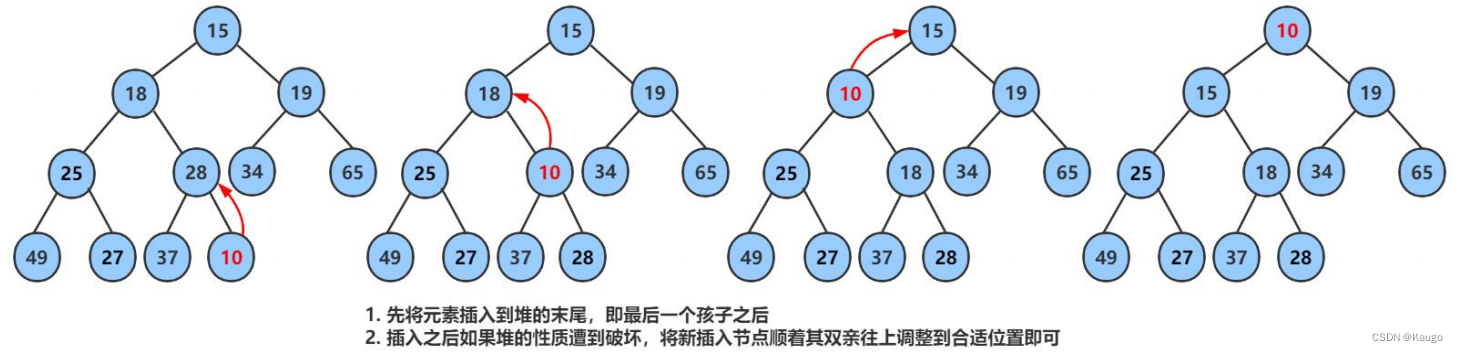
图片是小堆，我们代码是大堆

void HeapPush(HP* php, HPDataType x) {
	assert(php);
	if (php->size == php->capacity) {//判断容量是否够用
		//不够用则进行扩容
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * (php->capacity) * 2);
		if (tmp == NULL) {
			perror("realloc");
			return;
		}
		//判断新的空间地址是否为空
		php->a = tmp;//把新容量的地址给我们堆
		php->capacity *= 2;
		//容量别忘了改
	}
	php->a[php->size] = x;//插入在最后
	php->size++;
	//当前大小加一
	AdjustUp(php->a, php->size-1);
	//从新的元素下标位置向上调整让他回到正确位置
}

2.6堆的删除（HeapPop）

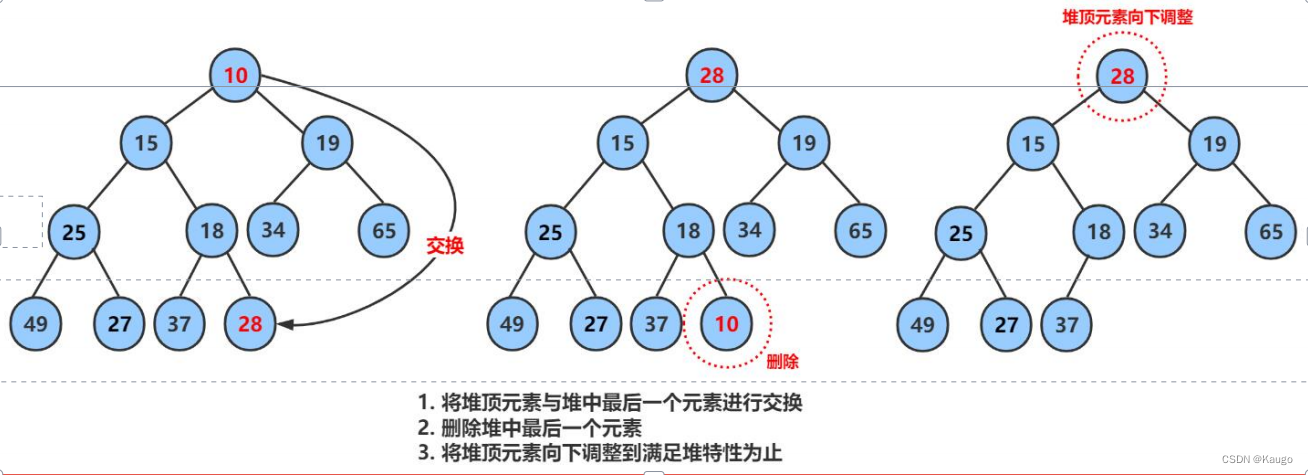
图片是小堆，代码是大堆

void HeapPop(HP* php) {
	assert(php);
	assert(!HeapEmpty(php));
	//判断是否大小为空
	Swap(&php->a[0], &php->a[php->size - 1]);
	//交换第一个与最后一个数据
	php->size--;//大小减一
	AdjustDown(php->a, php->size, 0);
	//从第一个数据位置向下调整
	//让其回到其正确位置
}

2.7堆的首元素（HeapTop）

HPDataType HeapTop(HP* php) {
	assert(php);
	assert(!HeapEmpty(php));
	return php->a[0];
}

2.8堆的大小（HeapSize）

int HeapSize(HP* php) {
	assert(php);
	return php->size;
}

`

三、堆排序

3.1把给的数据建成一个堆

1.向上建堆，时间复杂度为O(N*logN)

 for (int i = 1; i < size; i++) {
		AdjustUp(a, i);
	} 
	 //因为向上建堆的要求除了child位置其余位置构成堆
	 //所以我们只能从第二个数据开始调整，
	 //前两个数据构成堆我们再从第三个数据开始调整
	 //以此类推直到下标为size-1

2.向下建堆，时间复杂度为O（N）推荐！！！

for ( int i = (size - 1 - 1) / 2; i >= 0; i--) {
		//i刚开始为下标为（size-1）的父母
		AdjustDown(a, size, i);
	} 
	//向下调整条件左右都为堆，
	//所以我们从下开始调整，小范围到大范围
	//先把小范围都变成堆，然后逐渐扩大每次调整的数据个数
	//倒数从第一个非叶结点开始调整

3.2堆排序Heapsort

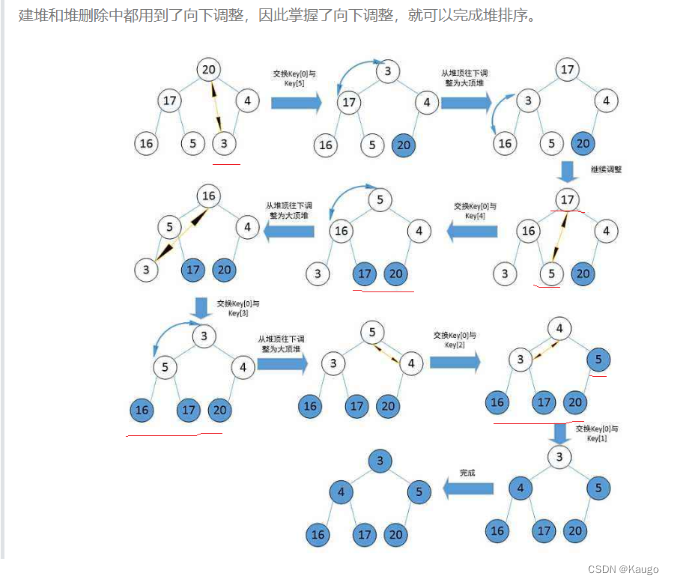
void HeapSort(int* a, int size) {
	for ( int i = (size - 1 - 1) / 2; i >= 0; i--) {
		//i刚开始为下标为（size-1）的父母
		AdjustDown(a, size, i);
	} 
	//向下调整条件左右都为堆，
	//所以我们从下开始调整，小范围到大范围
	//先把小范围都变成堆，然后逐渐扩大每次调整的数据个数
	//倒数从第一个非叶结点开始调整

	//要升序则要建大堆
	//要排成降序则要建小堆
	int end = size - 1;//最后一个元素下标为end
	while (end > 0) {
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
		//排好一次正确位置end要减一
	}
}