题目

剑指 Offer II 076. 数组中的第 k 大的数字

思路

假设有个划分函数divide：

• divide：将num在[l,r]范围内，按照nums[l]进行划分，返回一个数组range，划分为：

  • 所有小于nums[l]的数：移动到nums[l,range[0]-1] 中
  • 所有等于nums[l]的数：移动到nums[range[0],range[1]] 中
  • 所有大于nums[l]的数：移动到nums[range[1+1],r] 中

我们要找第k大的数，可以转化为求第nums.length - k + 1小的数

对nums在[0,nums.length-1]范围内做划分，结果为range：

• 如果k就在range的范围内，即 k >= range[0] && k <= range[1]，说明第k小的数就是nums[range[0]]

• 如果k < range[0]，说明第k小的数在前半段，即nums[0,range[0]-1]中，那就在这个范围内去递归处理

• 如果k > range[0]，说明第k小的数在后半段，即nums[range[1]+1,]中，那就在这个范围内去递归处理

最后看看divide怎么实现：

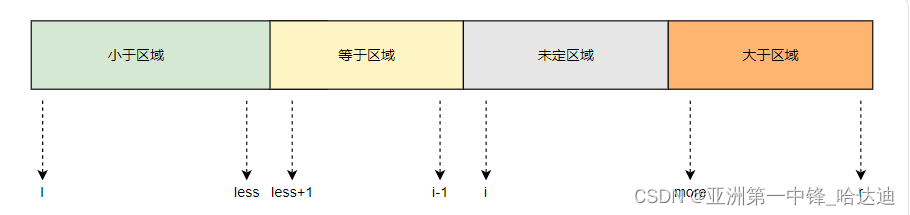
由于最终需要将数组nums在[l,r]范围内划分为4个区域，因此需要定义这3个区域的边界：

• 小于nums[l]的区域：[l+1,less]

  • 一开始所有区域的范围都是0，因此less初始化为l

• 等于nums[l]的区域：[less+1,i-1]

  • 等于区域一定紧跟着小于区域，因此左边界为less+1
  • 其右端点为当前遍历的位置的前一个位置，也就是i-1
  • i会初始化为l+1，因此等于区域的初始范围也是0个元素

• 大于nums[l]的区域：[more,r]

  • 因为需要初始化为0个元素，因此more初始化为r+1

• 最后还剩下一个未定区域：[i,more-1]

接着从l+1开始遍历每个元素i，如果

• nums[ i ]等于nums[l] ：什么都不用处理，i++

• nums[ i ]小于nums[l] ：将nums[i]和等于区域的第一个数交换，将小于区域的右边界less++

  • 实质是扩充小于区域
  • 交换过来的数等于nums[l]，因此i++，继续后面的循环
  • 这样操作后，整个数组依旧维持4个区域的定义

• nums[ i ]大于于nums[l] ：将nums[i]和大于区域的前一个数交换，将大于区域的左边界–

  • 实质是扩充大于区域
  • 此时由于不清楚交换过来的数和nums[l]的关系，因此需要重新进入循环
  • 这样操作后，整个数组依旧维持4个区域的定义

什么时候结束循环呢？

当i和more相撞的时候，表示数组中所有的数都遍历过了，且都在正确的位置上

代码

class Solution {

    public int findKthLargest(int[] nums, int k) {
             k = nums.length - k + 1 -1 ;
            int l = 0;
            int r = nums.length-1;
            while(true) {
                int[] range = divide(nums,l,r);
                if(k >= range[0] && k <= range[1]) {
                    return nums[k];
                }
                if(k < range[0]) {
                    r = range[0]-1;
                } else {
                    l = range[1] + 1;
                }
            }
    }

     private int[] divide(int[] nums,int l,int r) {
            if(l == r) {
                return new int[]{l,l};
            }
            int p = nums[l];
            // 大于[more,r]
            int more = r + 1;
            // 小于[l+1,less]
            // 等于[less+1,i-1]
            int less = l;
            int i = l + 1;
            for(;i<more;){
                if(nums[i] < p){
                    swap(nums,i,less+1);
                    i++;
                    less++;
                } else if(nums[i] > p) {
                    swap(nums,i,more-1);
                    more--;
                } else {
                    i++;
                }
            }
            // 等于区域 [less+1,i-1]
            swap(nums,l,less);
            return new int[]{less,i-1};
        }


        private void swap(int[] nums,int a,int b) {
            int temp = nums[a];
            nums[a] = nums[b];
            nums[b] = temp;
        }
}