1.问题背景与描述

赛题分析：这道题出的比较好，考察面较多，难度循环渐进，相对C题是比较有层次的一道题

2.解题思路分析

2.1 问题一的分析

请从收货量、发货量、快递数量增长/减少趋势、相关性等多角度考虑，建立数学模型，对各站点城市的重要程度进行综合排序，并给出重要程度排名前5的站点城市名称。

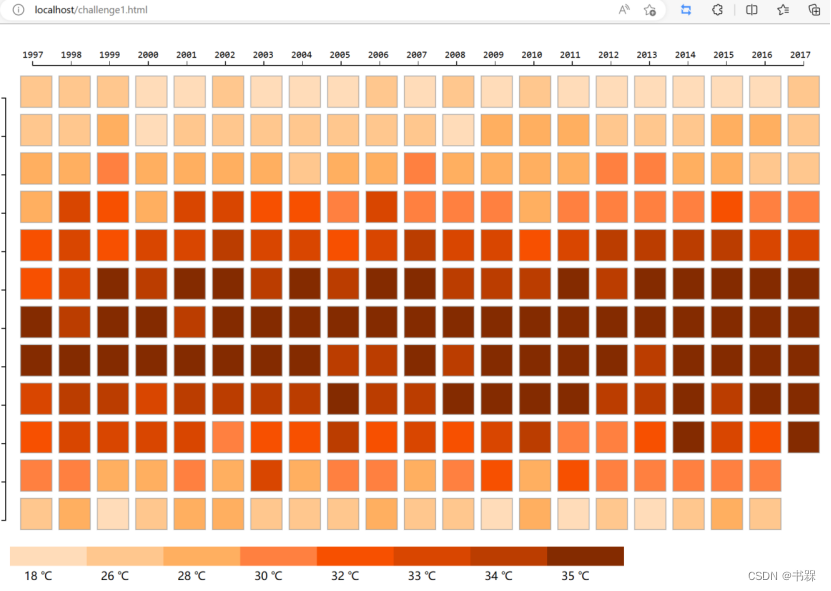
第一问比较简单，先对附件1的快递数据进行数据分析，分别对这些指标进行可视化研究，进一步利用已给的数据计算出城市对应的收货量、发货量、快递数量增长/减少趋势、相关性等特征指标。然后建立Pearson相关性分析，单因素方差分析等模型进行定量数据分析。最后建立综合评价模型对站点城市进行综合排序。综合评价模型可以选用主成分得分评价，TOPSIS综合评价等方法。

2.2 问题二的分析

建立数学模型，预测2019年4月18日和2019年4月19日各“发货-收货”站点城市之间快递运输数量，以及当日所有“发货-收货”站点城市之间的总快递运输数量，并在表2中填入指定的站点城市之间的快递运输数量，以及当日所有“发货-收货”站点城市之间的总快递运输数量。

要求利用附件一数据建立预测模型，来预测运输量，可以建立机器学习回归模型比如SVR，随机森林等来训练数据。当然最重要的一步是特征工程，需要对涉及到的特征变量进行热编码，然后在跑模型训练就好了，随遇涉及到的时间序列可以转化为时间序列特征参与模型训练。

2.3 问题三的分析

附件2为该快递公司记录的2020年4月28日—2023年4月27日的快递运输数量。由于受到突发事件影响，部分城市之间快递线路无法正常运输，导致站点城市之间无法正常发货或收货(无数据表示无法正常收发货，0表示无发货需求)。请利用附件2数据，建立数学模型，预测2023年4月28日和2023年4月29日可正常“发货-收货”的站点城市对(发货城市-收货城市)，并判断表3中指定的站点城市对是否能正常发货，如果能正常发货，给出对应的快递运输数量，并将结果填入表3。

要求建立数学模型来预测是否可正常发货，并且可发货城市还要预测对应的发货数量。是否可发货时布尔变量，也就是分类变量，本质上是个分类问题，根据历史数据来预测未来的分类，就是个分类器训练问题，这就简单了。当然训练好的机器学习模型的前提是较好的特征工程，这里可以做的地方就多了。贝叶斯分类器，逻辑回归分类器等等可以尝试不同模型根据验证数据集上表现来选择好的分类器。
可发货城市还要预测对应的发货数量，参考问题二思路；

2.4 问题四的分析

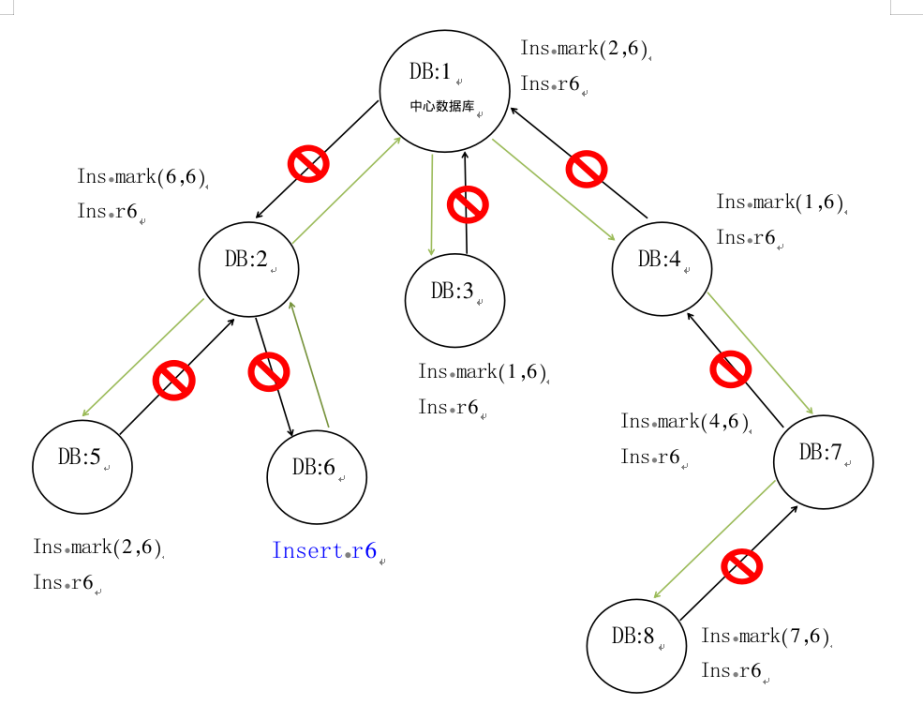
图1给出了所有站点城市间的铁路运输网络，铁路运输成本由以下公式计算：。在本题中，假设实际装货量允许超过额定装货量。所有铁路的固定成本、额定装货量在附件3中给出。在运输快递时，要求每个“发货-收货”站点城市对之间使用的路径数不超过5条，请建立数学模型，给出该快递公司成本最低的运输方案。利用附件2和附件3的数据，计算该公司2023年4月23—27日每日的最低运输成本，填入表4。

这道题就是典型的物流运输优化问题，最经典的优化类型题了，所以我说这道题出得好，真的就是能考的知识点都有了，厉害厉害。

目标函数：成本最低 Min W
决策变量：收发货的运输方案Xij；
约束条件：

• 1.站点城市对之间使用的路径数不超过5条
• 2.额定装货限制
• 3.固定成本优化
  本质上是一个0-1整数优化模型，可以利用LINGO编程或者matlab求解。

2.5 问题五的分析

请利用附件2中的数据，不考虑已剔除数据、无发货需求数据、无法正常发货数据，解决以下问题。
(1) 建立数学模型，按季度估计固定需求常数，并验证其准确性。将指定季度、指定“发货-收货”站点城市对的固定需求常数，以及当季度所有“发货-收货”城市对的固定需求常数总和，填入表5。
(2) 给出非固定需求概率分布估计方法，并将指定季度、指定“发货-收货”站点城市对的非固定需求均值、标准差，以及当季度所有“发货-收货”城市对的非固定需求均值总和、非固定需求标准差总和，填入表5。

这道题的发挥空间比较大，涉及参数估计和概率学的东西，第一个小问题可以用问题三的机器学习预测模型去解决，不过数据需要按照季度的时间维度。当然也可以用一些比如EM估计算法来求解
第二小问可以用常用的概率分布进行数据拟合，比如正态分布，对数正态分布，泊松分布等，看看拟和效果确定参数分布值

3.完整代码+结果分享

博主刚拿到题，先分享具体解题思路，数据收集和完整代码，快的话大概晚上会分享出来