目录
一、迪杰斯特拉算法
1. 术语定义
2. 算法描述
3. 举例说明
4. 构建从源节点到目的节点的路径
5. 构建最低费用路径树
6. 构建转发表
二、距离向量路由算法
1. 术语定义
2. 举例说明
3. 距离向量表
4. 更新距离向量表
5. 举例说明
三、距离向量路由算法 PLUS
1. 链路费用改变与链路故障
2. 毒性逆转
3. 毒性逆转的 BUG
四、LS 算法和 DV 算法比较
1. 消息复杂度
2. 收敛速度
3. 健壮性
一、迪杰斯特拉算法
迪杰斯特拉算法属于 LS 算法。
1. 术语定义

2. 算法描述

3. 举例说明
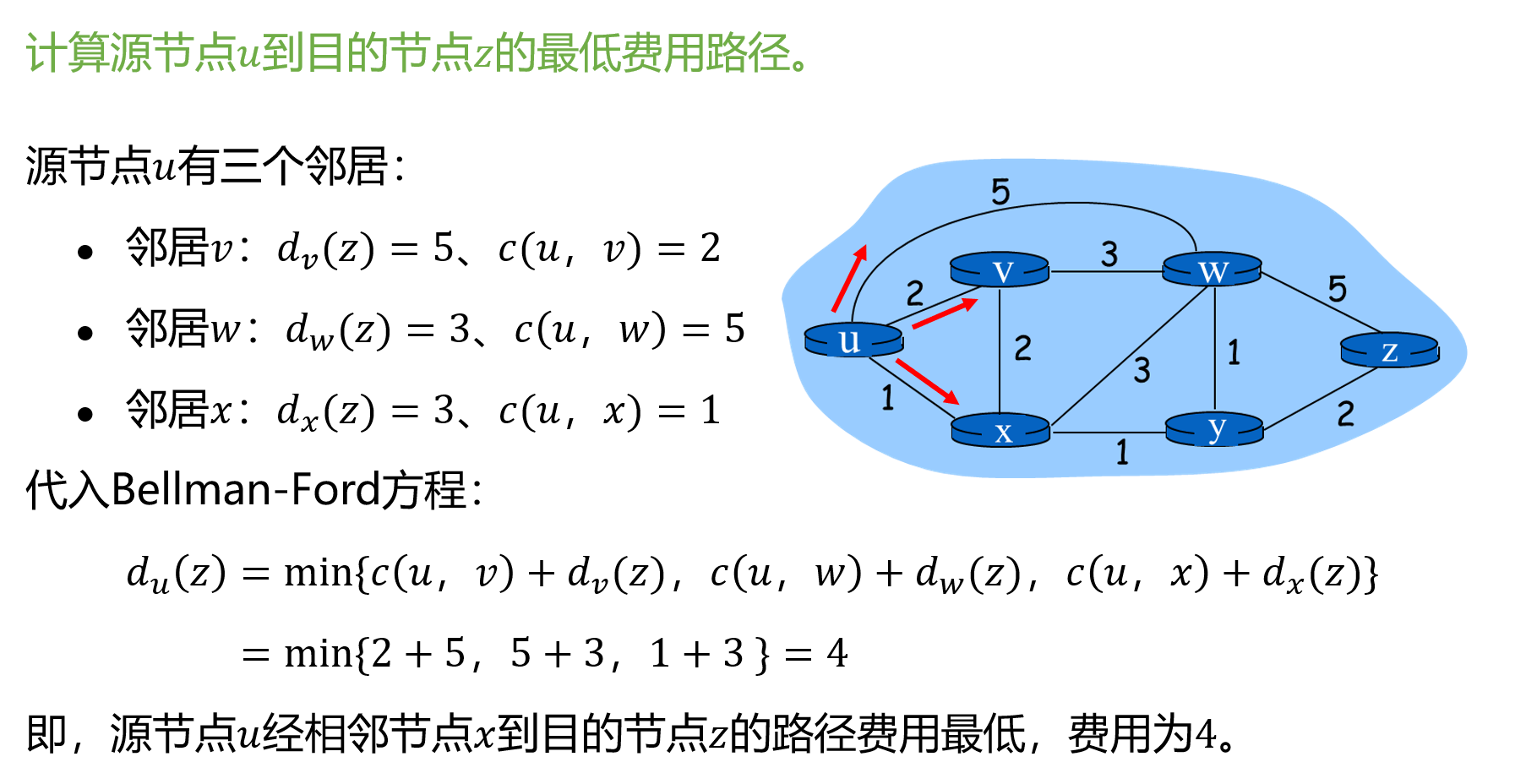
计算从 u 到所有可能目的节点的最低费用路径。
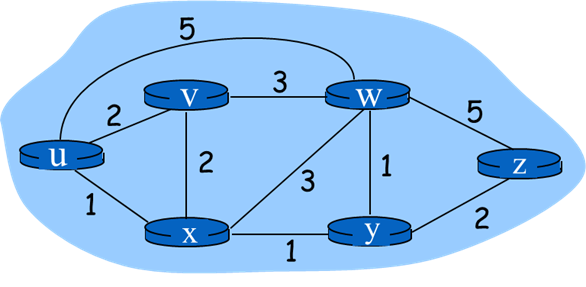
计算过程如表,表中的每一行表示一次迭代结束时的算法变量值。
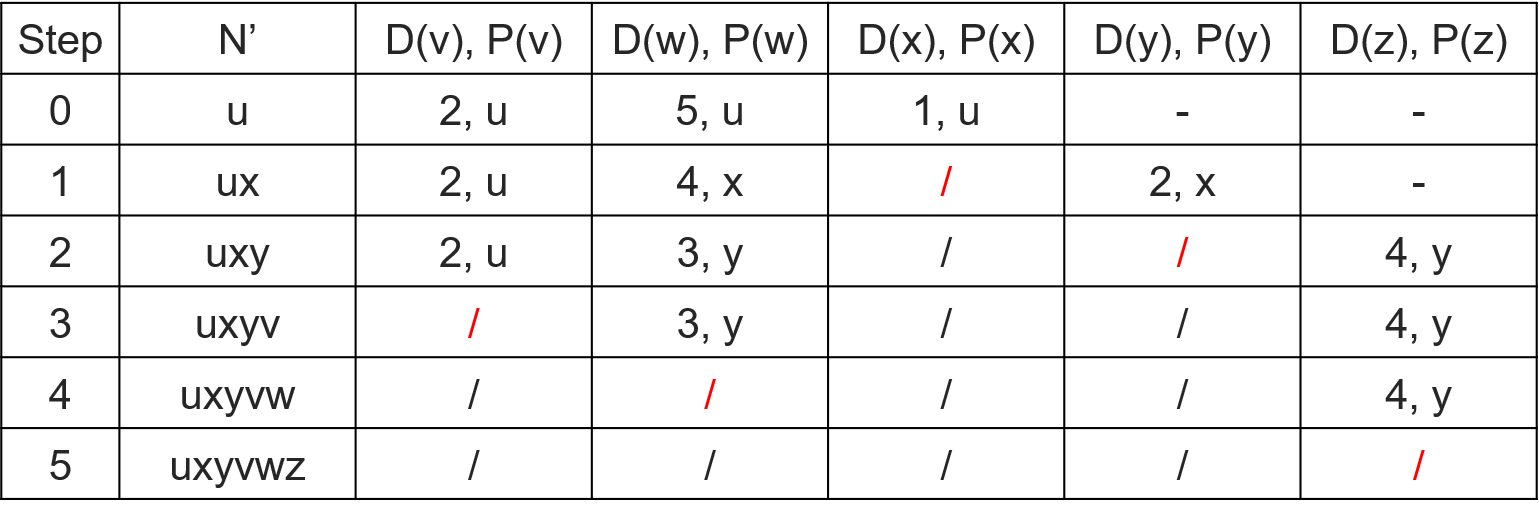
- 代表无穷,/ 代表已经加入集合 N' 。
4. 构建从源节点到目的节点的路径
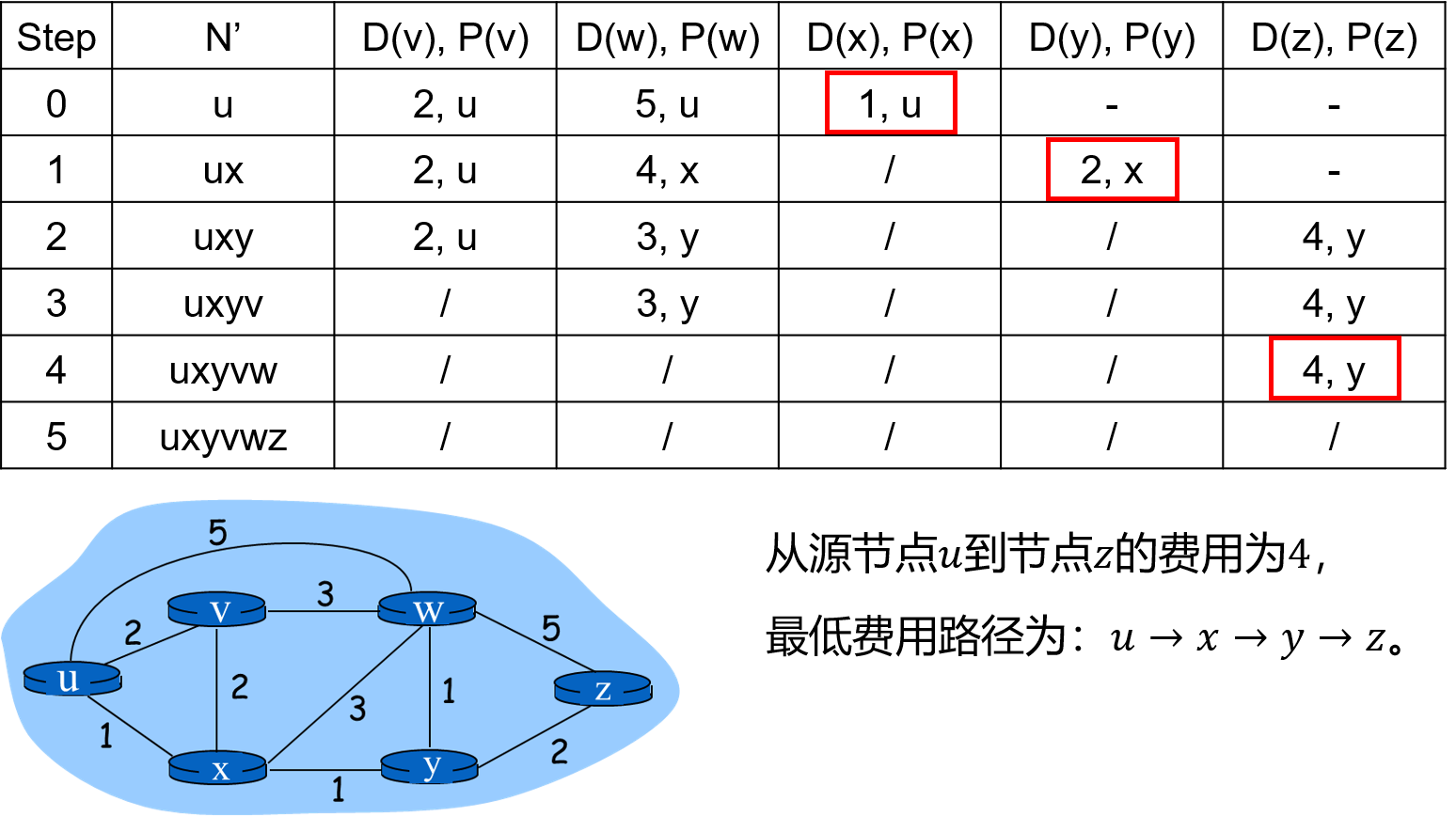
5. 构建最低费用路径树
最低费用路径树不同于最小生成树。最小生成树保证连接所有节点的路径权值之和最小,而最低费用路径树只是保证源节点到各目的节点的路径权值之和最小。因此,最小生成树不用指出一个源节点,而最低费用路径树必须指出一个源节点。源节点的不同,会导致最低费用路径树的不同。
根据目的节点找出顺序及其前驱节点,可以画出从源节点 u 到所有目的节点的最低费用路径树。

根据得到的最低费用路径树,可以生成源节点 u 的转发表。
6. 构建转发表
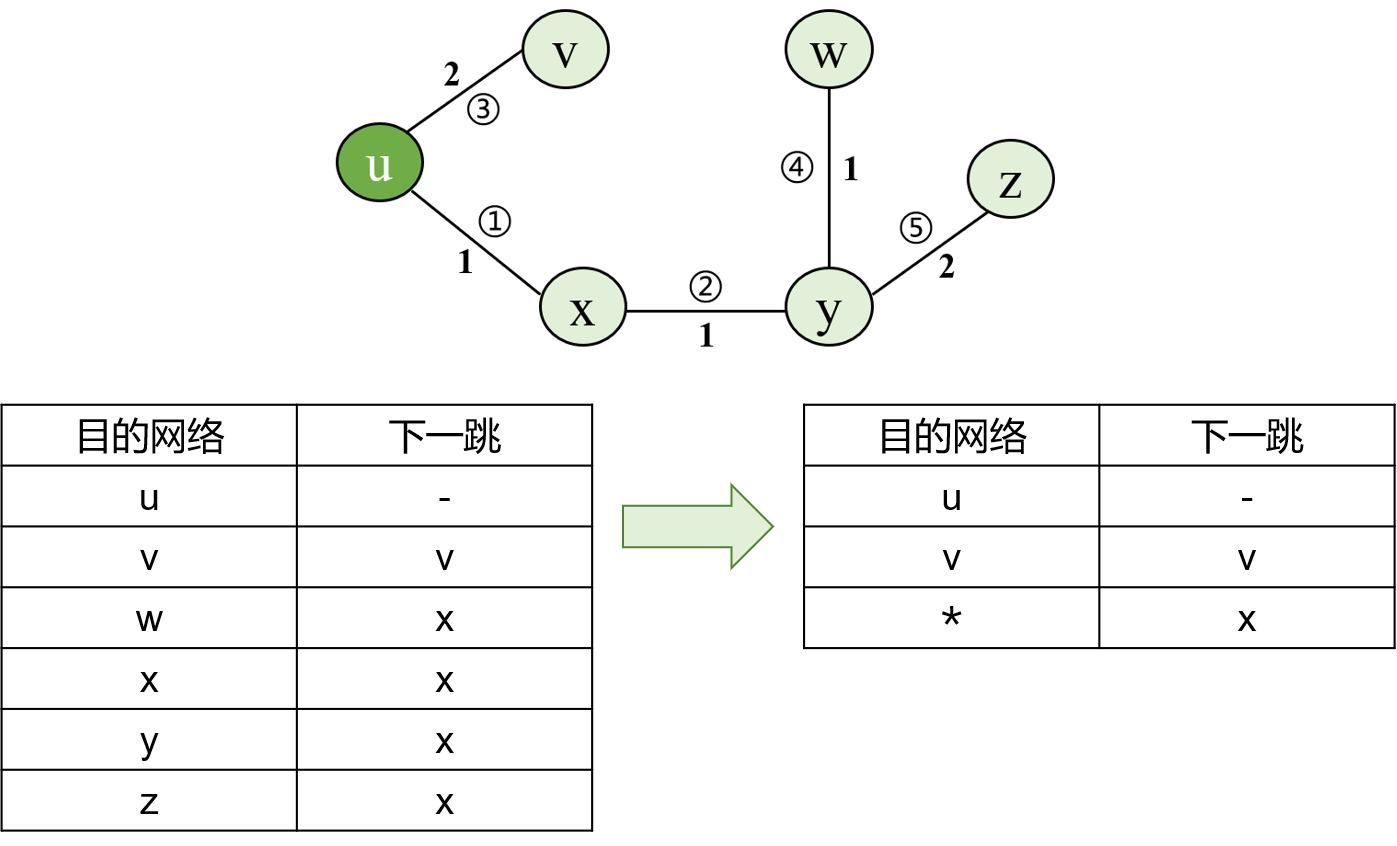
默认路由 * :用于表示所有具有相同下一跳的表项。即将下一跳相同的项合并为一项,用 * 表示目的节点。默认路由的优先级最低:转发分组时,只有找不到对应表项时,才使用默认路由。
二、距离向量路由算法
1. 术语定义
最低费用路径的费用表示

2. 举例说明
所有 d 值都是邻居节点告诉源节点的,源节点只知道它与邻居节点的直接链路的链路费用。
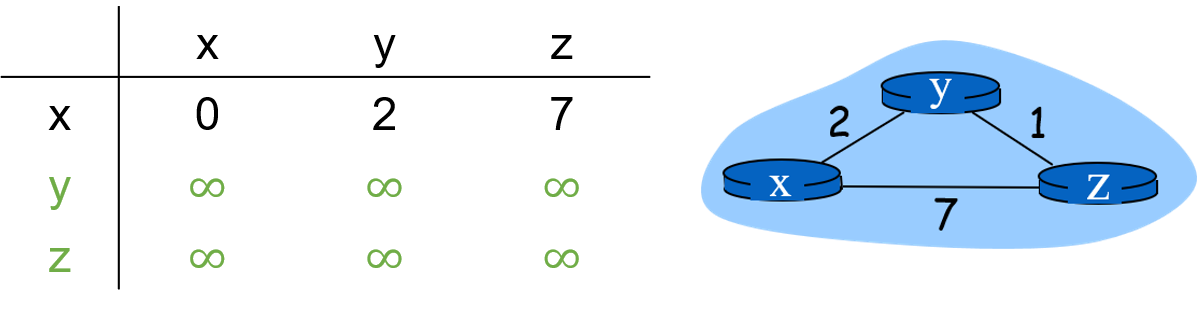
3. 距离向量表

初始时 x 并不知道 y 和 z 的距离向量,因此都设置为无穷。
4. 更新距离向量表

5. 举例说明
初始节点只知道自己到邻居节点的链路费用。

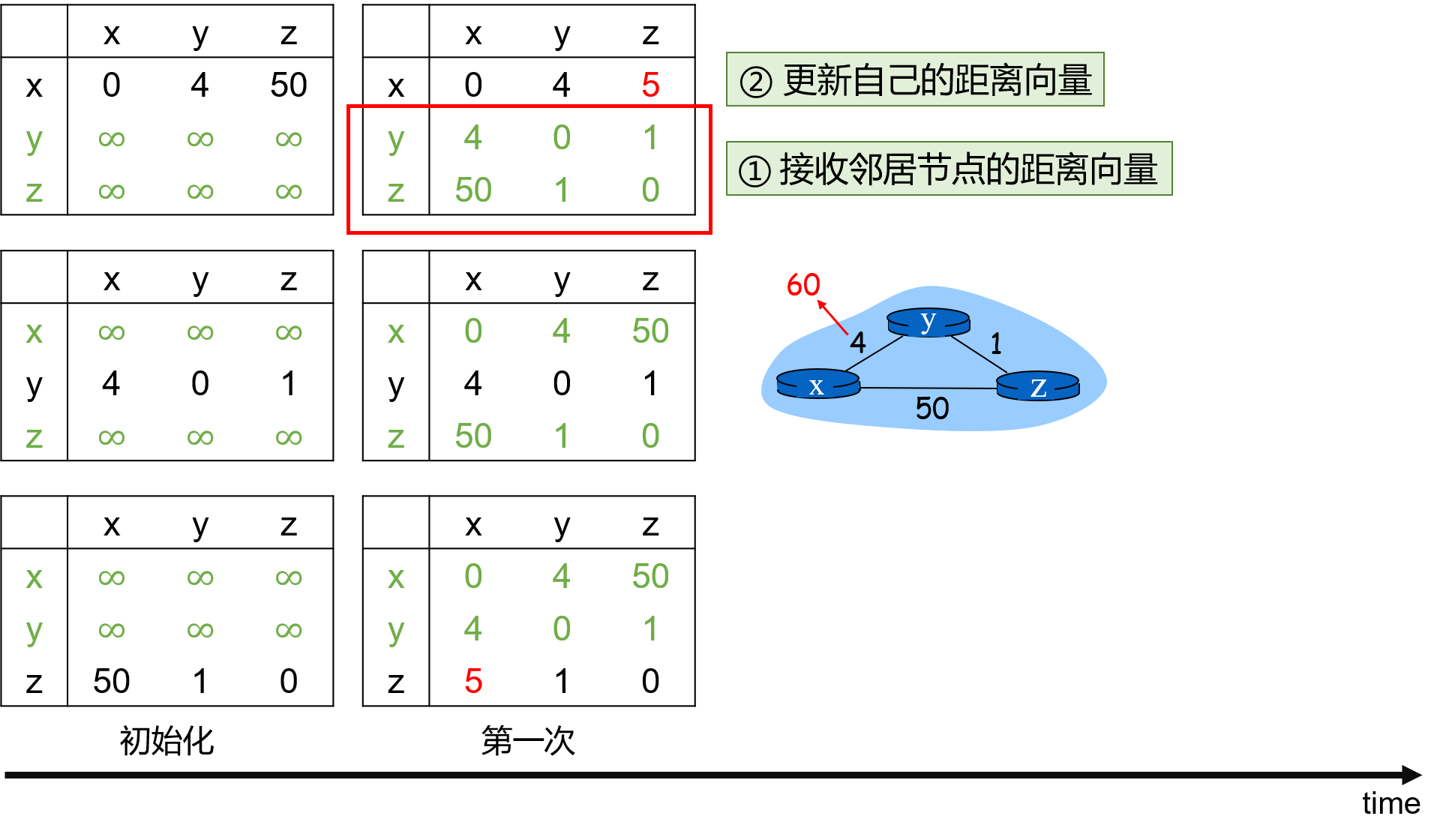
开始后,节点将自己的距离向量表发送给邻居,同时接收邻居的距离向量表。然后,根据邻居的距离向量表来更新自己的距离向量。
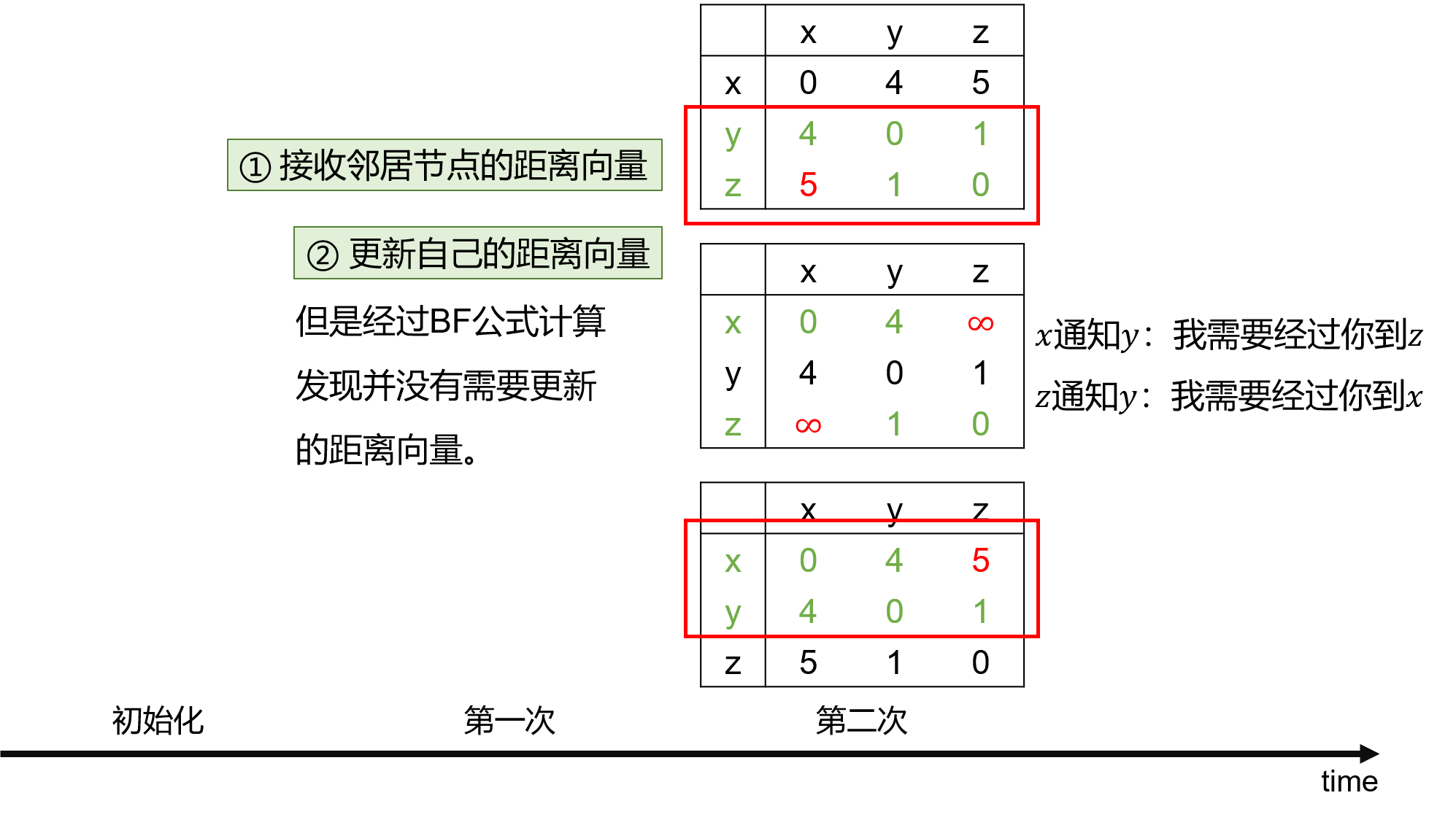
注意:c(x, z) 等数值来源于图,Dy 和 Dz 来源与邻居的距离向量表。此外,这一时刻的 Dx 由 BF 公式计算而得,跟上一时刻的 Dx 值无关(不需要和上一时刻的 Dx 值比大小)!因此,更新的 Dx 值可能更大也可能更小。

只要自己的距离向量更新了,就需要发送给自己的邻居节点,同时也要接收邻居节点发来的更新的距离向量。
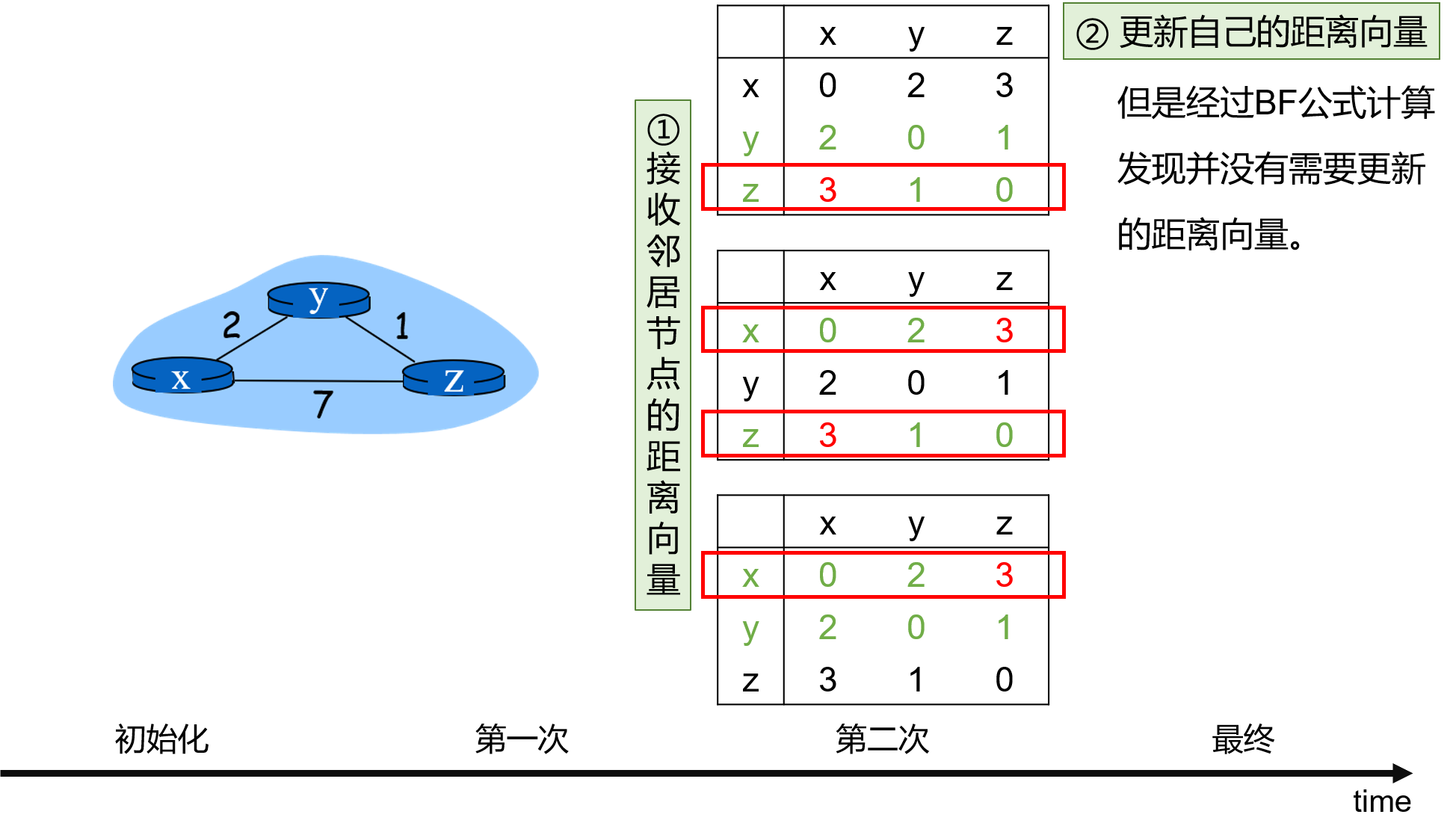
第二次没有需要更新的距离向量,因此不会再发送给邻居节点,从而算法终止。

总结:
① 多次重复从邻居节点接收更新的距离向量,并重新计算距离向量,再向邻居节点发送更新的距离向量,一直持续到没有更新的距离向量发出为止。
② 算法进入暂时的静止状态,直到某个链路的费用发生改变为止。
③ 再次重复 ① 的操作。
三、距离向量路由算法 PLUS
1. 链路费用改变与链路故障
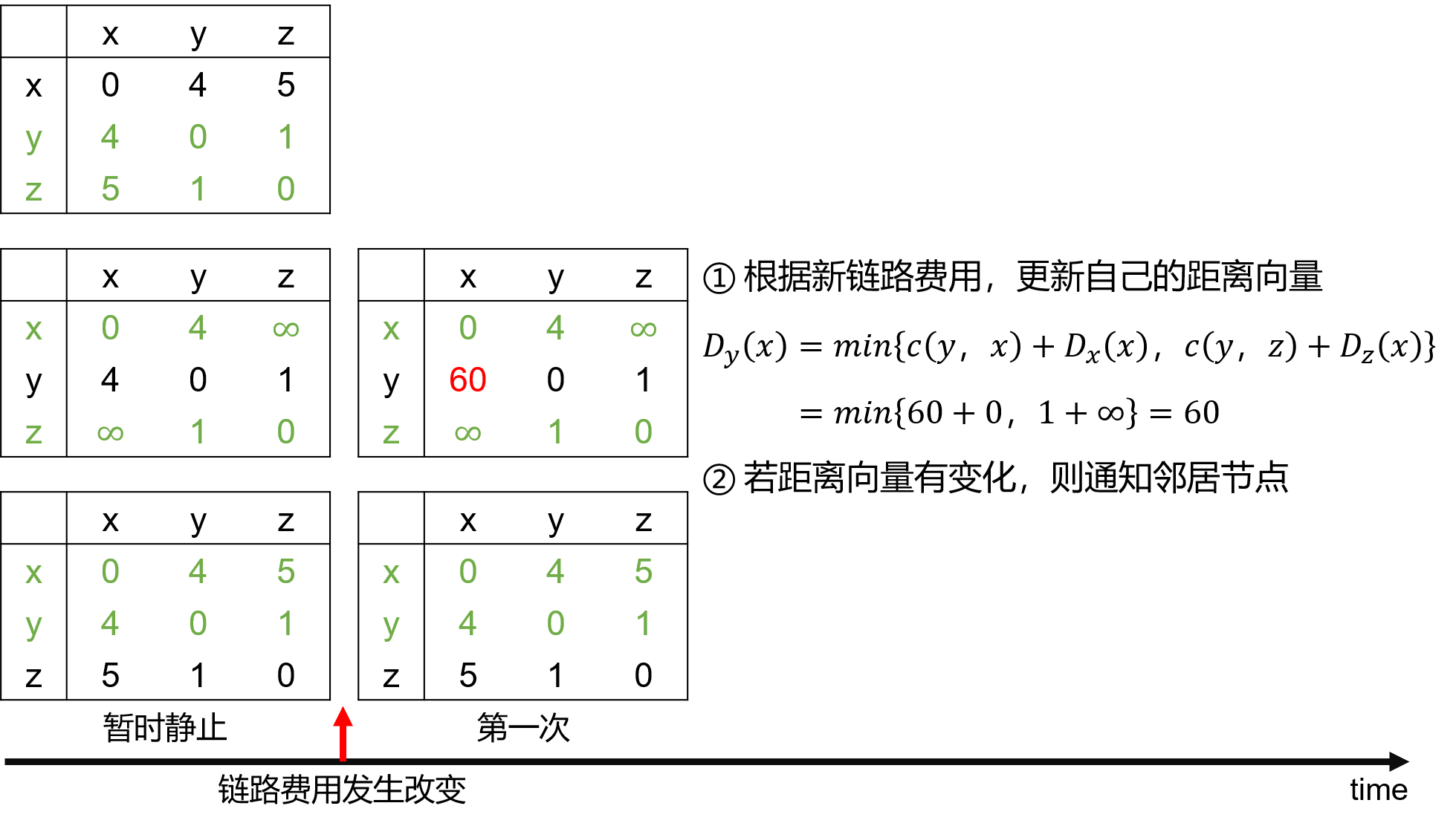
当一个节点检测到它与邻居节点之间的链路费用发生变化时,就用 BF 公式重新计算其距离向量。若距离向量发生变化,则通知其邻居节点。
(1)某链路费用减少时的情况
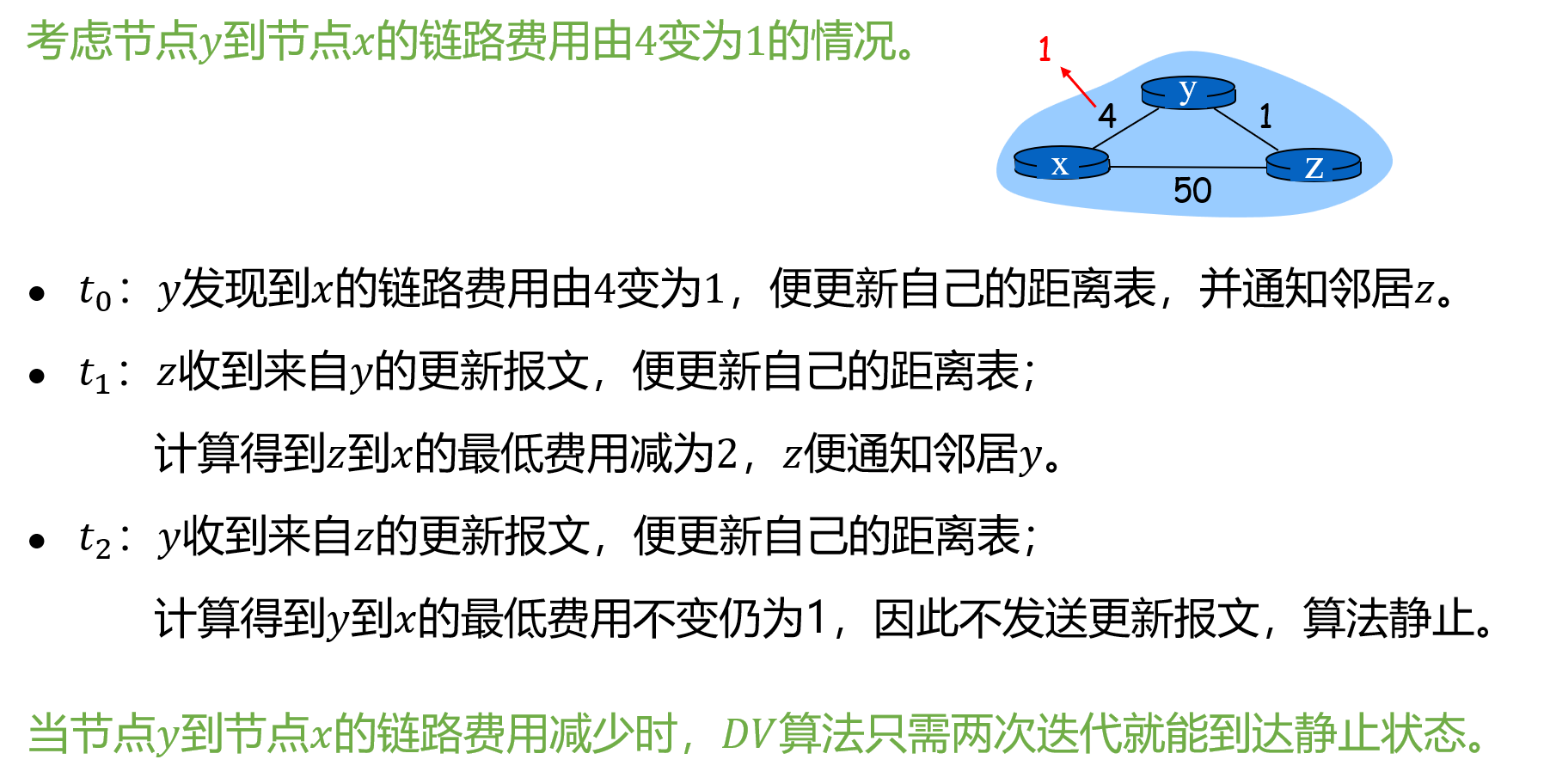
说明:节点之间链路费用减少的 好消息 在网络中能迅速传播。
(2)某链路费用增加时的情况
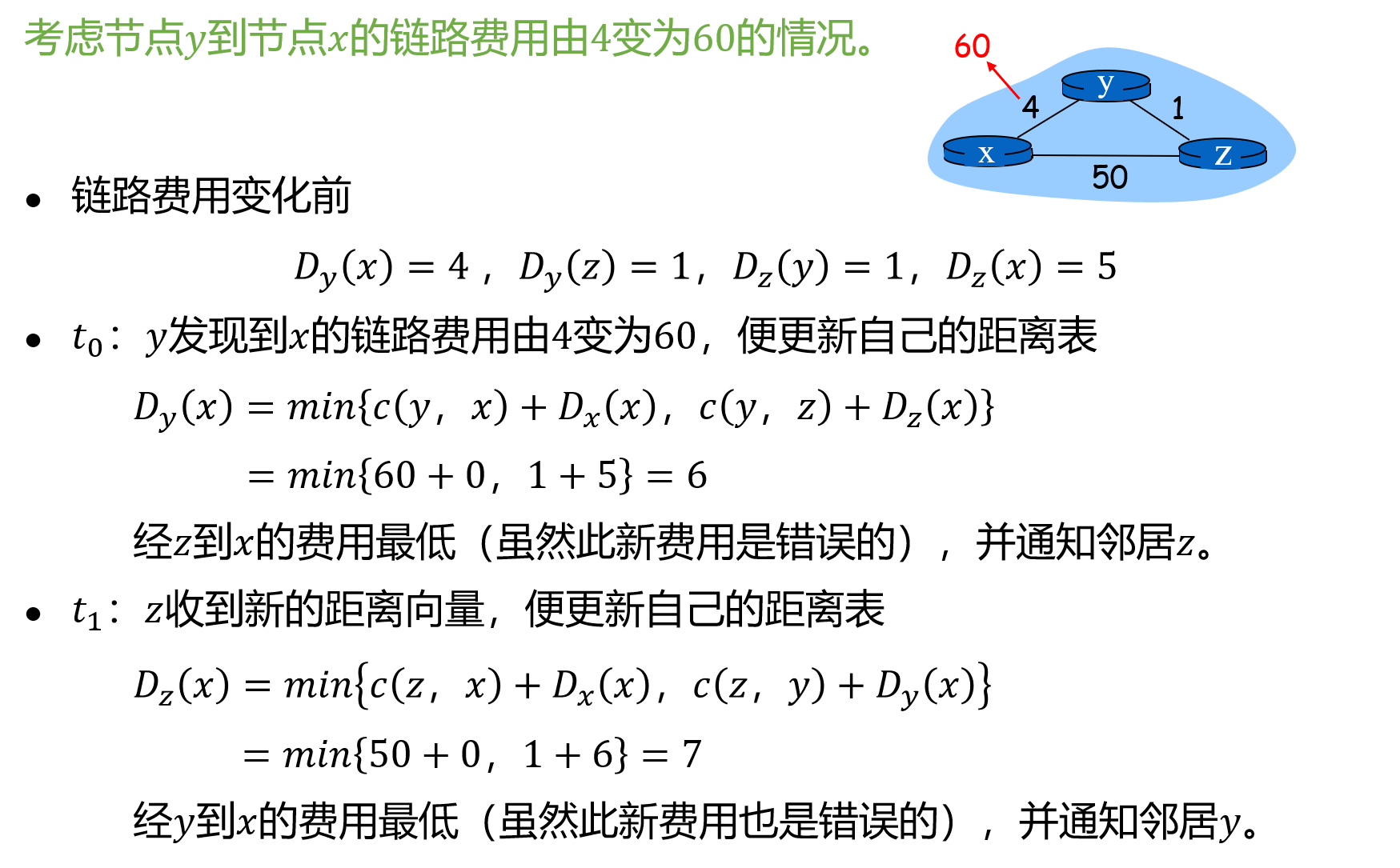
Q:为什么计算出来的新费用是错的?
A:由于链路费用改变,Dz(x) 已经不等于 5 了,但 y 还是使用了旧的 Dz(x) 。

产生选路回环:为到达 x, y 通过 z 选路,z 又通过 y 选路。即目的地为 x 的分组到达 y 或 z 后,将在这两个节点之间不停地来回反复,直到转发表发生新的改变为止。

说明:链路费用增加的 坏消息 传播得很慢!当链路费用增加的很大时,会出现 计数到无穷 问题。如链路费用 c(y,x) 变为 10000,c(z,x) 变为 9999 时。
2. 毒性逆转
解决 计数到无穷 的方法:毒性逆转。
毒性逆转:假如 z 为了实现最低路径费用而需要通过 y 去到达 x,则 z 告诉 y :它到 x 的距离是无穷大的,从而 y 将不会再经过 z 到 x 。
假设 y 计算出它到达 x 的最低费用路径为:y→z→...→x,而 z 计算出它到达 x 的最低费用路径为:z→y→...→x,则会产生选路循环。因此,如果 z 到 x 需要经过 y,则让 y 到 x 的时候一定不要经过 z,因为无论如何 y 经 z 到 x 的费用都会比 y 到 x 的大(因为 z 到 x 包含了 y 到 x)
y 内心 OS:还不如俺自己去找 x 。
前两步还是和之前一样的操作,不过引入毒性逆转后,x 或 y或 z 需要根据自己的下一跳来通知邻居节点其某个距离向量为无穷。
链路费用的改变打破了原本的安宁!
z 根据 y 更新的距离向量来更新自己的距离向量。

虽然 z 的距离向量改变了,但由于该路径还是会经过 y,对于 y 仍应该是无穷,因此不必再通知 y 了,从而又进入了暂时静止状态。
3. 毒性逆转的 BUG
Q:毒性逆转可以完全解决计数到无穷的问题吗?
A:不能。如果是三个以上节点的环路,则不能被毒性逆转技术检测到。
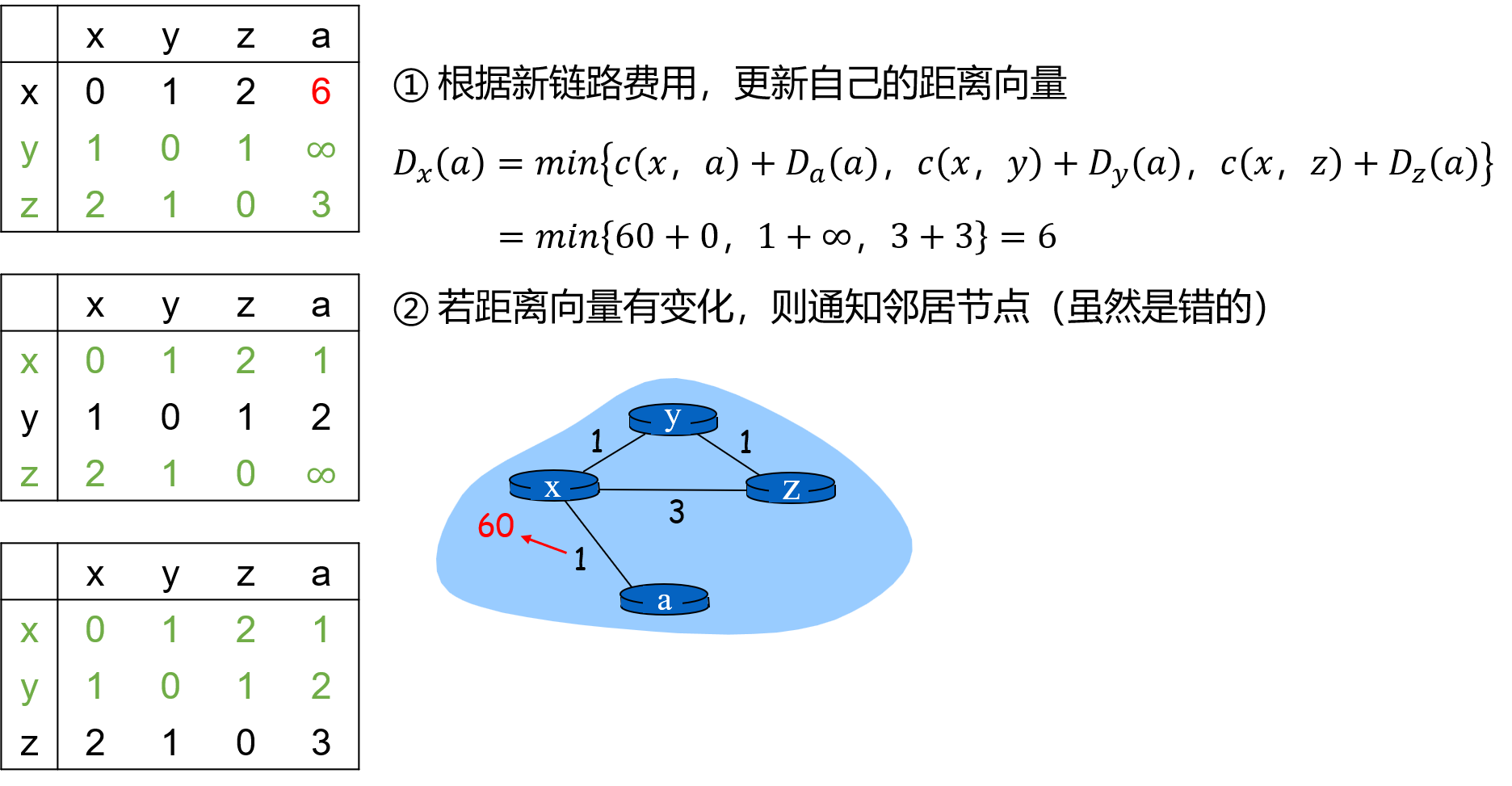
Dz(a) 的路径为:z→y→...→a,进一步这条路为:z→y→x→...→a,但是 z 只知道自己的下一跳是谁,而不知道自己的下一跳又去经过了 x,因此基于下一跳的毒性逆转策略失效了。
其它解决环路的方法:
- 定义最大度量,以防止计数至无穷大
- 抑制计时器
- 水平分割
- 路由毒化
- 触发更新
四、LS 算法和 DV 算法比较
1. 消息复杂度
LS 算法:知道网络每条链路的费用,需发送 O(nE) 个报文;当一条链路的费用变化时,必须通知所有节点。
DV 算法:迭代时,仅在两个直接相连邻居之间交换报文;当链路费用改变时,只有该链路相连的节点的最低费用路径发生改变时,才传播已改变的链路费用。
2. 收敛速度
LS 算法:需要 O(nE) 个报文和 O(n2) 的搜寻,可能会振荡。
DV 算法:收敛较慢。可能会遇到选路回环,或计数到无穷的问题。
3. 健壮性
Q:当一台路由器发生故障、操作错误或受到破坏时,会发生什么情况?
LS 算法:路由器向其连接的一条链路广播不正确费用,路由计算基本独立(仅计算自己的转发表),有一定健壮性。
DV 算法:一个节点可向任意或所有目的节点发布其不正确的最低费用路径,一个节点的计算值会传递给它的邻居,并间接地传递给邻居的邻居。一个不正确的计算值会扩散到整个网络。