DFIG控制11: 磁链定向矢量控制和仿真,主要是看下怎么根据DFIG模型来做矢量控制。
磁链定向和模型简化
原模型
dq同步坐标系下的模型:DFIG控制10: 双馈发电机的动态模型_Fantasy237的博客
电压方程:
{
u
s
d
=
R
s
i
s
d
+
d
d
t
ψ
s
d
−
ω
e
ψ
s
q
u
s
q
=
R
s
i
s
q
+
d
d
t
ψ
s
q
+
ω
e
ψ
s
d
u
r
d
=
R
r
i
r
d
+
d
d
t
ψ
r
d
−
ω
s
1
ψ
r
q
u
r
q
=
R
r
i
r
q
+
d
d
t
ψ
r
q
+
ω
s
1
ψ
r
d
\begin{cases} u_{sd} &= R_si_{sd}+\frac{d}{dt}\psi_{sd}-\omega_e\psi_{sq}\\ u_{sq} &= R_si_{sq}+\frac{d}{dt}\psi_{sq}+\omega_e\psi_{sd}\\ u_{rd} &= R_ri_{rd}+\frac{d}{dt}\psi_{rd}-\omega_{s1}\psi_{rq}\\ u_{rq} &= R_ri_{rq}+\frac{d}{dt}\psi_{rq}+\omega_{s1}\psi_{rd} \end{cases}
⎩
⎨
⎧usdusqurdurq=Rsisd+dtdψsd−ωeψsq=Rsisq+dtdψsq+ωeψsd=Rrird+dtdψrd−ωs1ψrq=Rrirq+dtdψrq+ωs1ψrd
磁链方程:
{
ψ
s
d
=
L
s
i
s
d
+
L
M
i
r
d
ψ
s
q
=
L
s
i
s
q
+
L
M
i
r
q
ψ
r
d
=
L
r
i
r
d
+
L
M
i
s
d
ψ
r
q
=
L
r
i
r
q
+
L
M
i
s
q
\begin{cases} \psi_{sd} &=L_si_{sd}+L_Mi_{rd}\\ \psi_{sq} &=L_si_{sq}+L_Mi_{rq}\\ \psi_{rd} &=L_ri_{rd}+L_Mi_{sd}\\ \psi_{rq} &=L_ri_{rq}+L_Mi_{sq} \end{cases}
⎩
⎨
⎧ψsdψsqψrdψrq=Lsisd+LMird=Lsisq+LMirq=Lrird+LMisd=Lrirq+LMisq
磁链方程简化
磁链定向后,定子磁链与d轴重合,如下图左。电压定向后,定子电压和q轴重合。稳态下,两种定向方式的最终得到的磁链和电压的角度差异不大,但是模型不同。这里只介绍稳态下的磁链定向矢量控制。
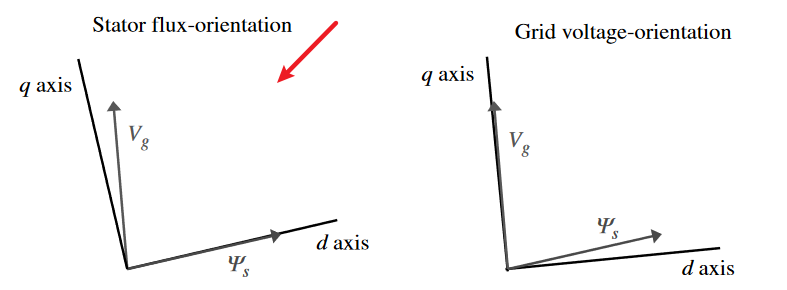
磁链方程得到简化,定子磁链只有d轴分量,q轴分量为0。因为变换器连接在转子侧,能控制的是转子电压(从而间接控制转子电流和定子电流),因此先把转子磁链都用转子电流表示,消去定子电流:
ψ
s
d
=
L
s
i
s
d
+
L
M
i
r
d
=
ψ
s
→
i
s
d
=
ψ
s
L
s
−
L
M
L
s
i
r
d
ψ
s
q
=
L
s
i
s
q
+
L
M
i
r
q
=
0
→
i
s
q
=
−
L
M
L
s
i
r
q
ψ
r
d
=
(
L
r
−
L
M
2
L
s
)
i
r
d
+
L
M
L
s
ψ
s
ψ
r
q
=
L
r
i
r
q
−
L
M
2
L
s
i
r
q
\begin{align*} \psi_{sd} &=L_si_{sd}+L_Mi_{rd}=\psi_{s} \rightarrow i_{sd}=\frac{\psi_{s}}{L_{s}}-\frac{L_{M}}{L_{s}}i_{rd}\\ \psi_{sq} &=L_si_{sq}+L_Mi_{rq}=0 \rightarrow i_{sq}=-\frac{L_{M}}{L_{s}}i_{rq}\\ \psi_{rd} &=\left(L_{r}-\frac{L_{M}^{2}}{L_{s}}\right)i_{rd}+\frac{L_{M}}{L_{s}}\psi_{s}\\ \psi_{rq} &=L_ri_{rq}- \frac{L_{M}^{2}}{L_{s}}i_{rq} \end{align*}
ψsdψsqψrdψrq=Lsisd+LMird=ψs→isd=Lsψs−LsLMird=Lsisq+LMirq=0→isq=−LsLMirq=(Lr−LsLM2)ird+LsLMψs=Lrirq−LsLM2irq
电压方程简化
稳态时,定子磁链幅值不变,微分为0,并且忽略绕组的压降,对定子电压方程再做简化。可以根据
u
s
q
u_{sq}
usq来简单估计磁链幅值。定子电压大约超前定子磁链90°,因此定子电压矢量大致在q轴附近。
u
s
d
=
R
s
i
s
d
+
d
d
t
ψ
s
d
−
ω
e
ψ
s
q
≈
0
u
s
q
=
R
s
i
s
q
+
d
d
t
ψ
s
q
+
ω
e
ψ
s
d
≈
ω
e
ψ
s
d
\begin{align*} u_{sd} &= R_si_{sd}+\frac{d}{dt}\psi_{sd}-\omega_e\psi_{sq}\approx 0\\ u_{sq} &= R_si_{sq}+\frac{d}{dt}\psi_{sq}+\omega_e\psi_{sd}\approx \omega_e\psi_{sd}\\ \end{align*}
usdusq=Rsisd+dtdψsd−ωeψsq≈0=Rsisq+dtdψsq+ωeψsd≈ωeψsd
把前面的简化磁链表达式代入转子电压方程,并代入漏磁系数
σ
L
r
=
L
r
−
L
M
2
L
s
\sigma L_{r}= L_{r}- \frac{L_{M}^{2}}{L_{s}}
σLr=Lr−LsLM2:
u
r
d
=
R
r
i
r
d
+
σ
L
r
d
i
r
d
d
t
−
ω
s
1
σ
L
r
i
r
q
+
(
L
M
L
s
d
d
t
ψ
s
≈
0
)
u
r
q
=
R
r
i
r
q
+
σ
L
r
d
i
r
q
d
t
+
ω
s
1
σ
L
r
i
r
d
+
ω
s
1
L
M
L
s
ψ
s
\begin{align*} u_{rd} &= R_ri_{rd}+ \sigma L_{r}\frac{d i_{rd}}{dt}-\omega_{s1}\sigma L_{r}i_{rq}+ \left(\frac{L_{M}}{L_{s}}\frac{d}{dt}\psi_{s}\approx 0 \right)\\ u_{rq} &= R_ri_{rq}+\sigma L_{r}\frac{d i_{rq}}{dt}+\omega_{s1}\sigma L_{r}i_{rd}+\omega_{s1}\frac{L_{M}}{L_{s}} \psi_s \end{align*}
urdurq=Rrird+σLrdtdird−ωs1σLrirq+(LsLMdtdψs≈0)=Rrirq+σLrdtdirq+ωs1σLrird+ωs1LsLMψs
可以看到,转子的d轴电压和dq轴的电流都有关,q轴电压也是这样,存在耦合关系。
电流环
以d轴为例,根据电压方程,写出电压到电流的传递函数:
i
r
(
s
)
u
r
d
(
s
)
+
ω
s
1
σ
L
r
i
r
q
(
s
)
=
1
R
r
+
σ
L
r
s
\frac{i_{r}(s)}{u_{rd}(s)+\omega_{s1}\sigma L_{r}i_{rq}(s)}=\frac{1}{R_{r}+\sigma L_{r}s}
urd(s)+ωs1σLrirq(s)ir(s)=Rr+σLrs1
画成框图:
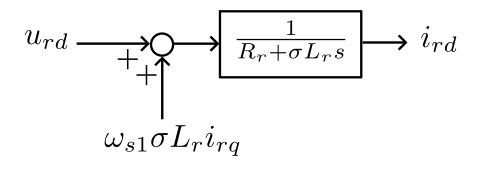
其中,
u
r
d
u_{rd}
urd是转子侧变换器输出的d轴转子绕组电压。目标是通过调节
u
r
d
u_{rd}
urd来控制转子电流
i
r
d
i_{rd}
ird。写出电流控制器的输出:
u
r
d
=
T
P
I
(
s
)
(
i
r
d
∗
−
i
r
d
)
−
ω
s
1
σ
L
r
i
r
q
u_{rd}=T_{PI}(s)(i_{rd}^{*}-i_{rd})-\omega_{s1}\sigma L_{r}i_{rq}
urd=TPI(s)(ird∗−ird)−ωs1σLrirq
其中包含了解耦项。把控制器也画进框图:

可以看到抵消耦合项后,就是一个二阶系统+PI控制器的形式,并且,在dq同步坐标系中,稳态下都是直流量。
另外可参考:DFIG控制6-b:电流环分析_Fantasy237的博客
q轴电流环也类似,只是解耦的表达式不同。其实也可以不加入解耦项,对稳态没有影响,只是动态性能比较差。
控制系统
控制系统如下,图片来自:H. Abu-Rub, M. Malinowski, and K. Al-Haddad, Power Electronics for Renewable Energy Systems, Transportation and Industrial Applications. John Wiley & Sons, 2014.
- dq轴的电流环和解耦,同上文描述。
- 通过PLL获得定子电压相位,根据定子电压和磁链相位的大致关系,减去90°,得到定子磁链相位 θ s \theta_{s} θs。
- 注意图中的 θ r \theta_{r} θr即转差角度 θ s 1 \theta_{s1} θs1,(转差角度=定子磁链角度-转子电角度)。(不想自己画图,导致记号有点混乱)。至于为什么park变换的角度是 θ s 1 \theta_{s1} θs1,可见:DFIG控制10: 双馈发电机的动态模型_Fantasy237的博客。大致的理解:由于转子两相坐标系和转子一起在旋转(角度为 θ r \theta_{r} θr),为了把转子的物理量从转子两相坐标系转换到dq同步坐标系(角度为 θ s \theta_{s} θs),需要补偿的角度是转差角 θ s 1 = θ s − θ r \theta_{s1}=\theta_{s}-\theta_{r} θs1=θs−θr。
- 注意控制时是把物理量的数值都换算到定子侧,但是最终的输出需要再换算到转子侧。

接下来的问题是:d轴和q轴的电流参考值怎么计算?
无功功率和d轴电流
这里的指的是定子侧的无功功率
Q
S
Q_{S}
QS。
因为定子电压基本和q轴重合(
u
s
=
u
s
q
,
u
s
d
=
0
u_{s}=u_{sq},\;u_{sd}=0
us=usq,usd=0),无功功率只和d轴电流有关:
Q
s
∗
=
3
2
u
s
q
i
s
d
=
3
2
u
s
q
(
ψ
s
L
s
−
L
M
L
s
i
r
d
∗
)
Q_{s}^{*}=\frac{3}{2}u_{sq}i_{sd}=\frac{3}{2}u_{sq}(\frac{\psi_{s}}{L_{s}}- \frac{L_{M}}{L_{s}}i_{rd}^{*})
Qs∗=23usqisd=23usq(Lsψs−LsLMird∗)
- 3/2的系数是因为使用了等幅值的Clarke变换。
- 无功功率取正值,因为按这个方向看,电压超前电流,为感性
根据之前得到的定子和转子电流的关系,可以根据定子无功功率的表达式来计算所需的转子d轴电流参考值。
有功功率和q轴电流
有功功率
定子侧的有功功率
P
s
P_s
Ps只和q轴电流有关,同样可以用转子电流来表示:
P
s
∗
=
3
2
u
s
q
i
s
q
=
−
3
2
L
M
L
s
u
s
q
i
r
q
∗
P_{s}^{*}=\frac{3}{2}u_{sq}i_{sq}=-\frac{3}{2}\frac{L_{M}}{L_{s}}u_{sq}i_{rq}^{*}
Ps∗=23usqisq=−23LsLMusqirq∗
根据所需的有功功率,可以计算转子q轴电流参考值。
转矩
另外,也可以根据所需的转矩来计算转子q轴电流参考值。
转矩公式见:DFIG控制10-b: 双馈发电机的转矩方程推导_Fantasy237的博客
使用与转子电流相关的表达式:
T
e
∗
=
1.5
n
p
L
M
L
s
(
ψ
s
q
i
r
d
−
ψ
s
d
i
r
q
)
=
1.5
n
p
L
M
L
s
(
−
ψ
s
d
i
r
q
∗
)
=
1.5
n
p
L
M
L
s
(
−
u
s
ω
e
i
r
q
∗
)
\begin{align*} T_{e}^{*}&= \frac{1.5n_{p}L_{M}}{L_{s}}(\psi_{sq}i_{rd}-\psi_{sd}i_{rq})\\ &= \frac{1.5n_{p}L_{M}}{L_{s}}(-\psi_{sd}i_{rq}^{*})\\ &= \frac{1.5n_{p}L_{M}}{L_{s}}(-\frac{u_{s}}{\omega_{e}} i_{rq}^{*}) \end{align*}
Te∗=Ls1.5npLM(ψsqird−ψsdirq)=Ls1.5npLM(−ψsdirq∗)=Ls1.5npLM(−ωeusirq∗)
最终的控制系统
加入电流参考值的计算,控制系统变为:
图片来自:G. Abad, J. Lopez, M. Rodriguez, L. Marroyo, and G. Iwanski, Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation. John Wiley & Sons, 2011.
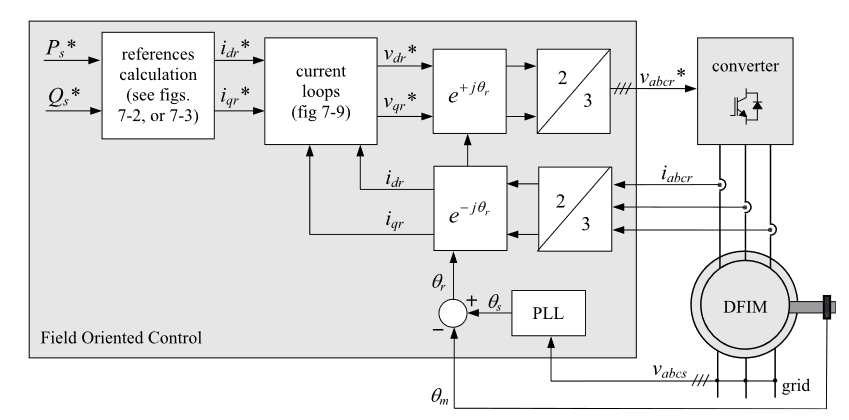
仿真模型
对应的仿真模型在:
- DFIG控制1:转子侧变换器控制_Fantasy237的博客
- DFIG控制3: 风机模型和最基础的MPPT_Fantasy237的博客