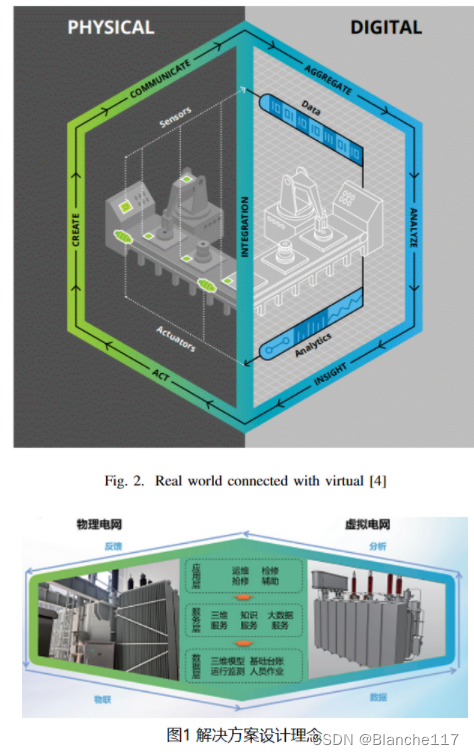
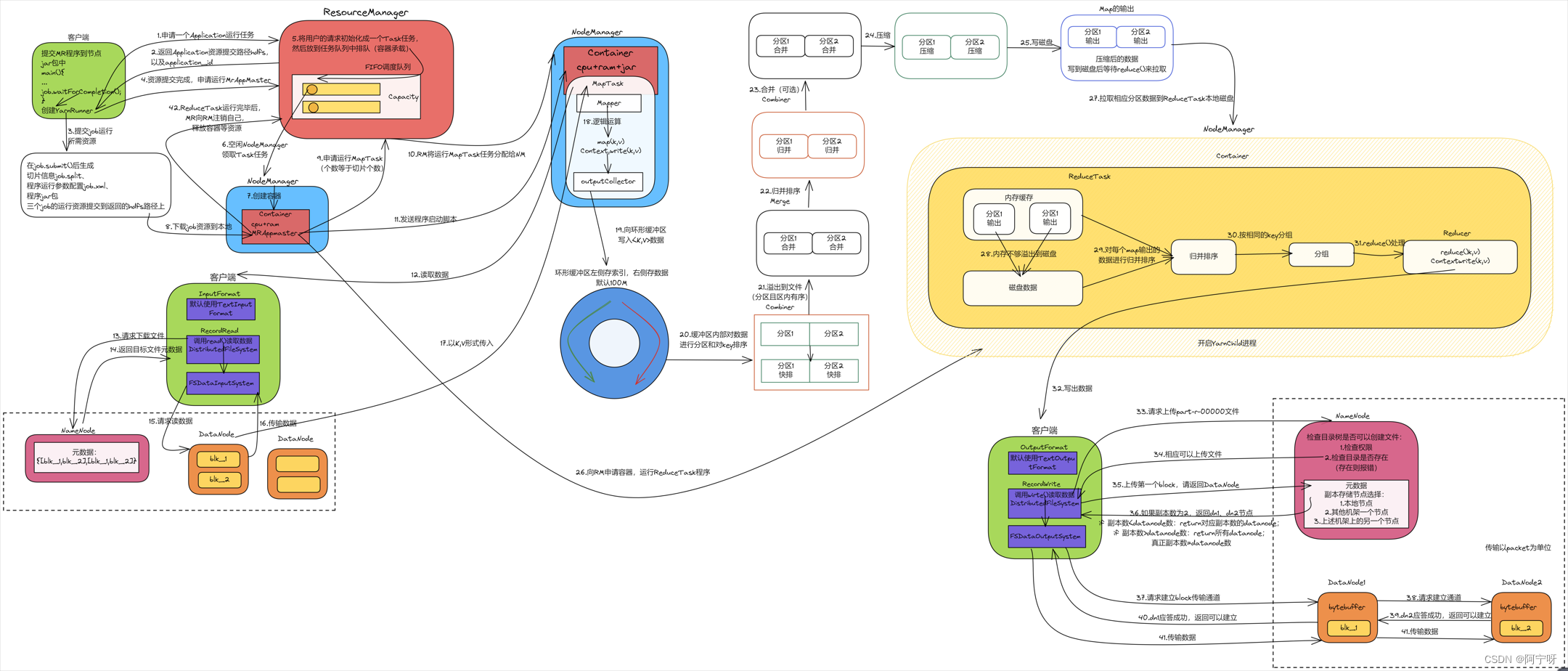
x.1 前言

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。是通过给定training dataset学习联合概率分布的方法，是一种生成方法。

x.2 使用贝叶斯定理做分类

使用贝叶斯定理做分类，相比较于朴素贝叶斯即丢除特征条件独立假设这个条件。

假设存在k类$c_1,c_2,...,c_k$，给定一个新实例$x=x^{(1)},...,x^{(n)}$，判断该实例来自哪一类。在判断来自哪一类即使用贝叶斯公式计算属于每一个类别的概率$P(Y=c_i|X=x)=\frac{P(Y=c_i)P(X=x|Y=c_i)}{P(X=x)}$，分母可以用全概率公式展开。接着依次计算属于每个类别的概率。

（下为贝叶斯公式：）

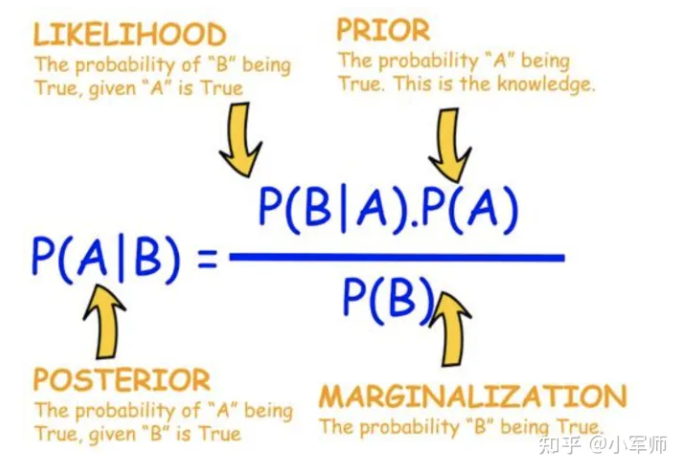
计算完后，取出类别概率最大的类别$c_j$，则属于$c_j$类。

x.3 使用朴素贝叶斯做分类

如果没理解的话，直接跳到x.6看例子。

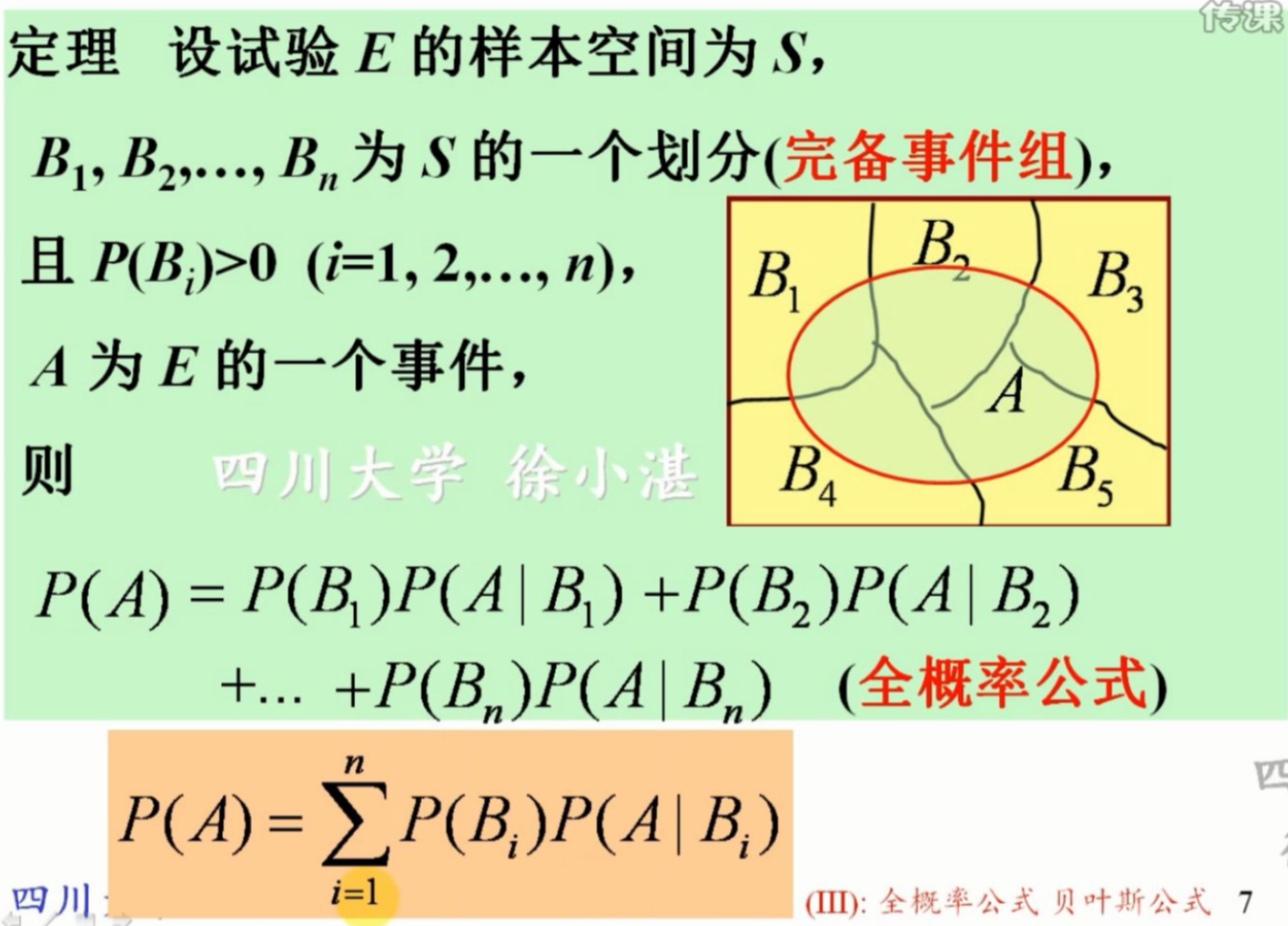
补充一下全概率公式，已知$B_1,...,B_n$是一个完备事件组且两两互斥：

在求取后验概率时，使用贝叶斯定理做变换后，得到式子$P(Y=c_i|X=x)=\frac{P(Y=c_i)P(X=x|Y=c_i)}{P(X=x)}$，分母用全概率公式展开，得到下式：

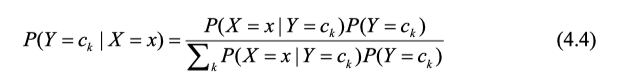
根据条件独立性假设推导条件概率展开式如下：

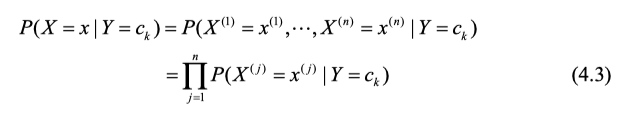
例如一个样本，它的特征取值是$x_j^{(1)},...,x_i^{(n)}$则你需要将这些值带入，就变成了上面第一行右边的式子，再根据独立性质展开即得(4.3)。

将(4.3)带入贝叶斯展开式(4.4)，得到如下式子：

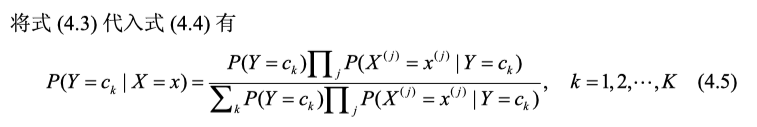
于是朴素贝叶斯分类器就变成了如下式：

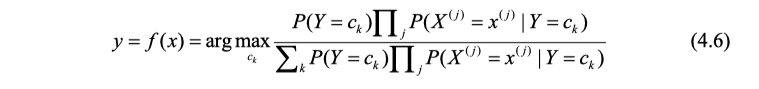
通过观察我们可以看到对于不同大类$c_k$，分母都是相同的，只要考察分子便可，于是将(4.6)化简得到如下：

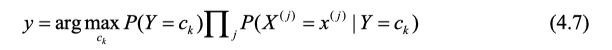
我们注意到最终的后验概率=先验概率*j个条件概率乘积。

x.4 后验概率最大化的含义

后验概率最大化的概率=期望风险最小化准则。这便是朴素贝叶斯采用的原理。详见统计学习分析4.1.2。

x.5 朴素贝叶斯法的参数估计

参数估计采用了Maximum Likelihood Estimation（MLE，极大似然估计）。极大似然估计即求让似然函数最大值的参数，在一堆样本中数数即等于极大似然估计法，为什么可以看下面的推导：

使用极大似然估计法求后验概率展开式分子中的先验概率和条件概率如下：

先验概率，直接数数便可得：

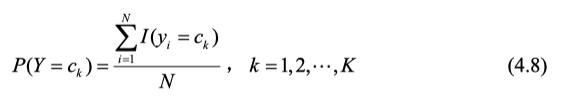
条件概率，使用条件概率展开式展开成乘积的格式，再数数可得：

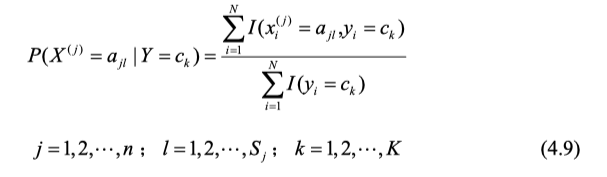
其中有j个特征，第j个特征有$S_j$个取值，y有k个大类。

x.6 朴素贝叶斯例子

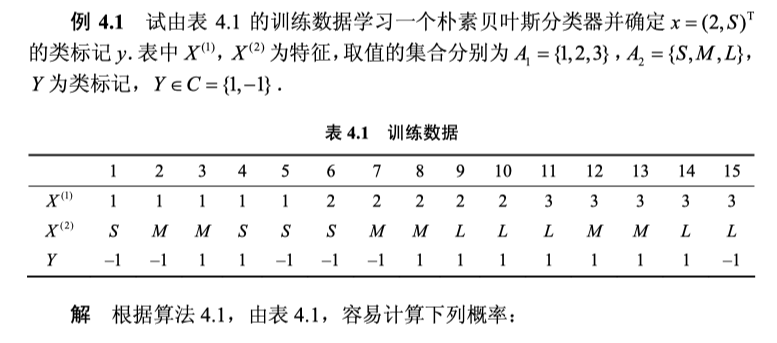
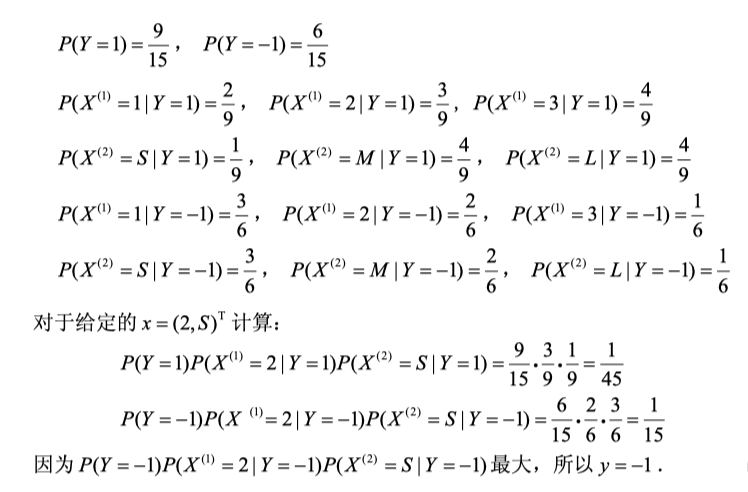
x.7 贝叶斯估计

即在参数估计时，用贝叶斯估计代替MLE。因为在例如用女儿国做样本，估计人群中男生比例时，往往会出现所要估计的概率值为0的情况，这时候会影响到后验概率的计算结果，使分类产生偏差，所以引入贝叶斯估计，如下：

如此便不会出现概率全0的情况。