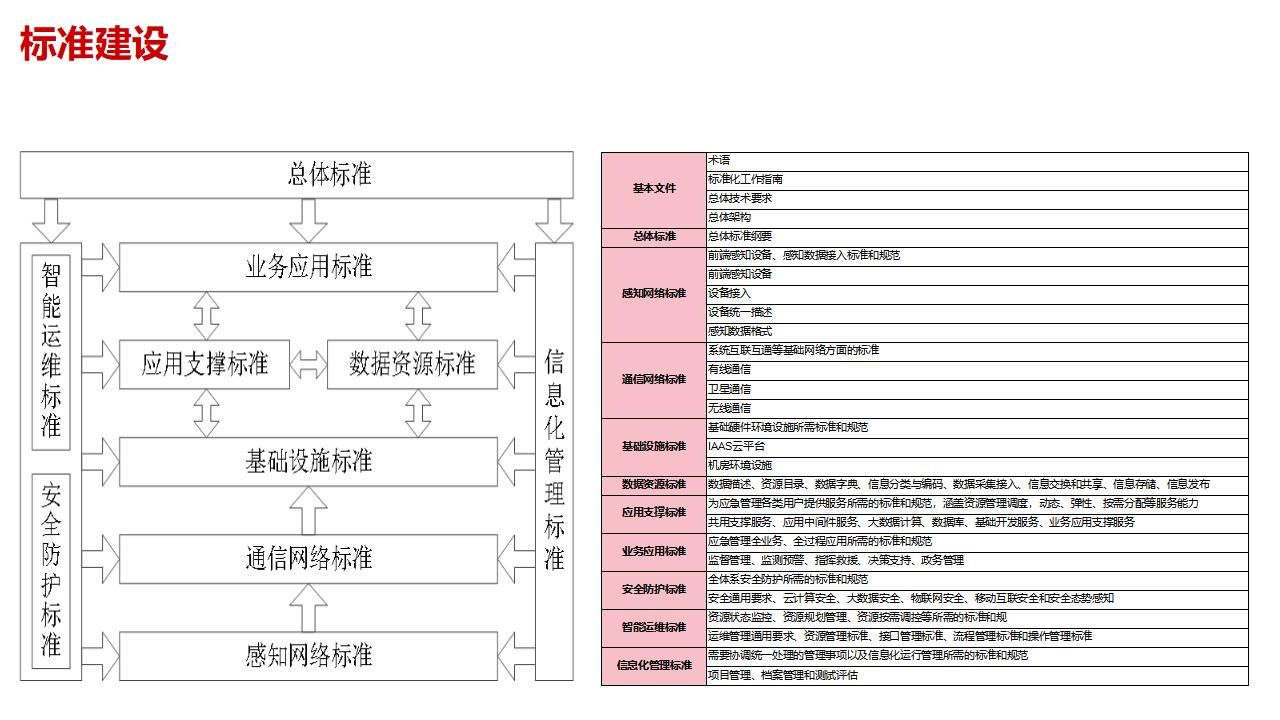
近年来,人工智能领域已经取得突破性进展,对经济社会各个领域都产生了重大影响,结合了统计学、数据科学和计算机科学的机器学习是人工智能的主流方向之一,目前也在飞快的融入计量经济学研究。表面上机器学习通常使用大数据,而计量经济学则通常使用较小样本,但这种区别日渐模糊,机器学习在经济学领域、特别是经济学与其它学科的交叉领域表现日益突出。R语言是用于统计建模的主流计算机语言,用于机器学习十分方便,且学习曲线相比于Python更加平滑,因此是进行机器学习的首选之一。
点击查看原文
一、理论基础与软件介绍
1.1 经济学基础原理
主要内容:
经济学思考范式,资源配置,效率与公平(古典经济学领域)。
格里高利·曼昆,通俗的讲述了十大经济学原理
例如,大卫·李嘉图的比较优势的原理。
例如,机会与成本。正U型定价曲线,MC(边际成本)ACT(平均总成本)

理性人假设,市场调节可能是最优解。
丹·艾瑞里 《怪诞行为学》 锚定效应
1.2 概率统计的基本思想
1.2.1 概率统计的常见概念
概率的诞生,奶茶问题。
正态分布。


置信区间

P值
1.2.2 评价(单指标评价与复合指标评价)
单指标评价:例如GDP
复合指数评价
指标体系评价

1.2.3 因果推断
概念产生:因果推断(Causal Inference)是根据某一结果发生的条件对因果关系作出刻画的过程,推断因果关系的最有效方法是进行随机对照试验,但这种方式耗时且昂贵、也无法解释和刻画个体差异;因此考虑从观察数据中进行因果推断,这类框架包括潜在结果框架和结构因果模型,下文对结构因果模型的因果推理方法进行综述。


证据等级,单个案例,多个案例,随机对照实验,循证,机理机制分析
1.3 机器学习用于评价和因果推断(算法介绍)
1.3.1KNN和Kmeans
KNN(K- Nearest Neighbor)法即K最邻近法,最初由 Cover和Hart于1968年提出,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路非常简单直观:如果一个样本在特征空间中的K个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

Kmeans


1.3.2德尔菲和AHP
德尔菲是Delphi的中文译名。美国兰德公司在20世纪50年代与道格拉斯公司合作研究出有效、可靠地收集专家意见的方法,以“Delphi”命名,之后,该方法广泛地应用于商业、军事、教育、卫生保健等领域。德尔菲法在医学中的应用,最早开始于对护理工作的研究,并且在使用过程中显示了它的优越性和适用性,受到了越来越多研究者的青睐。
AHP(Analytic Hierarchy Process)层次分析法是美国运筹学家T. L. Saaty教授于二十世纪70年代提出的一种实用的多方案或多目标的决策方法,是一种定性与定量相结合的决策分析方法。常被运用于多目标、多准则、多要素、多层次的非结构化的复杂决策问题,特别是战略决策问题,具有十分广泛的实用性。


1.3.3熵权法
TOPSIS-熵权法
熵权法是一种基于数据信息熵大小计算各个指标权重的方法,能很好的对多指标目标进行综合评价。TOPSIS法能进一步优化熵权法的结果,使评价结果更加客观合理[23~25]。
第一步,对数据进行标准化处理:

第二步,计算发展水平测度体系中的信息熵:

第三步,计算权重

第四步,构建测度指标的加权矩阵R:

第五步用加权矩阵R确定最优方案,最劣方案:

第六步,计算和最优最劣方案的距离和:

第七步,计算和理想方案的相对接近度:

理想接近度的值在[0-1]之间,其值越大,就代表该区域的畜牧业发展水平越高,反之则是该区域的畜牧业发展水平越低。
1.3.4随机森林算法
机器学习中有一种大类叫集成学习(Ensemble Learning),集成学习的基本思想就是将多个分类器组合,从而实现一个预测效果更好的集成分类器。集成算法可以说从一方面验证了中国的一句老话:三个臭皮匠,赛过诸葛亮。

1.3.4神经网络
神经网络学习分为两个阶段:一是多层前馈阶段,从输入层一次计算各层节点的实际输入、输出;二是反向修正阶段,即根据输出误差,沿路反向修正各连接权重,降低误差[27]。

为第层第个节点的输出值,为第层第个节点的激活值,为第层第个节点到第层第个节点的连接权重,为第层第个节点的阈值;为第层节点数,第为总层数,f(·)为神经元激活函数。
误差反向传播阶段采用梯度下降算法,使总误差向减少方向变化,计算公式为:

1.4 常用软件介绍
Excel,R,Stata,Photoshop,Arcgis,SPSS,Geoda,Python,Notexpress,Endnote
二、数据的获取与整理
2.1数据类型的介绍
定量数据,定类数据,
截面数据,时间序列数据,面板数据
2.2数据的获取
论文,统计局,年鉴,相关网站,购买
https://www.ceads.net.cn/

统计年鉴
论文标注
2.3数据的整理
常见的格式转换,缺失值的填补
三、常用评价方法与相关软件
3.1农业碳排放计算
3.2能源消费碳排放计算
3.3综合评价方法
公式的输入以及熵权法的实际操作
https://gongshi.wang/
3.4数据分析与数据可视化
常用数据可视化方法介绍
箱线图,柱状图,折线图,地理图形等
地理学三大定律与空间自相关分析
3.5随机森林回归建模
3.5.1模型构建与相关参数的优化
3.5.2模型的效果评估
3.5.3模型的结果分析
3.5.4驱动因素与机制机理分析(归因分析,驱动机制)
3.6神经网络回归建模
内容同上。
与其它模型效果对比
四、写作要点与案例
4.1整体写作要点
4.1.1好的开始是成功的一半(引言)
文章的选题来源
4.1.2文献综述的写法
4.1.3研究方法的选择与公式的编辑
4.1.4数据分析与可视化(分析)
4.1.5两种方式的写法
4.1.6结论与摘要的写法
4.1.7心态建设以及期刊选择与投稿
4.2案例
4.2.1两种常见类型论文的介绍
实验类型的文章介绍
模型计算类文章介绍
4.2.2案例
2000—2020年山西省农业碳排放时空特征及趋势预测
基于机器学习算法的新疆农业碳排放评估及驱动因素分析
西北地区碳排放的驱动因素与脱钩效应研究
中国农业高质量发展的地区差异及分布动态演进
点击查看原文