系列文章目录

剑指offer系列是一本非常著名的面试题目集，旨在帮助求职者提升编程能力和应对面试的能力。

文章目录

系列文章目录
@[TOC](文章目录)

前言
一、用两个栈实现队列
🔥 思路
🌈代码

二、青蛙跳台阶问题
🔥 思路
🌈代码

三、矩阵中的路径
🔥 思路
🌈代码

四、机器人的运动范围
🔥 思路
🌈代码

五、矩阵中的最长递增路径(难度: 困难)
🔥 思路
🌈代码

六、剪绳子Ⅰ（贪心）
🔥 思路
🌈代码

总结

前言

随着互联网行业的迅速发展和竞争的加剧，技术人才的需求量也越来越大，而面试已经成为求职过程中至关重要的一环。因此，掌握一定的面试技巧和解决问题的能力就变得至关重要。剑指offer系列汇集了许多公司常见的面试题目，并且针对每个问题都给出了详细的解答和分析，对于准备参加面试的求职者来说非常实用。在本系列文章中，我们将一步步地学习这些问题的解决方法，掌握如何在面试中优雅地回答这些问题，帮助读者更好地备战面试，拿到心仪的工作机会。

提示：以下是本篇文章正文内容，下面案例可供参考

一、用两个栈实现队列

⭐️⭐️⭐️
原题

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

示例 1：

输入：
["CQueue","appendTail","deleteHead","deleteHead","deleteHead"]
[[],[3],[],[],[]]

输出：[null,null,3,-1,-1]

示例 2：

输入：
["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
[[],[],[5],[2],[],[]]

输出：[null,-1,null,null,5,2]

提示：

1 <= values <= 10000 最多会对 appendTail、deleteHead 进行 10000 次调用

🔥 思路

首先，在定义 CQueue 时，我们创建了两个空栈：输入栈 inStack 和输出栈 outStack。

当需要向队列尾部添加元素时，我们调用 appendTail 函数，该函数会将元素插入到 inStack 的末尾。

当需要删除队列头部的元素时，我们调用 deleteHead 函数。该函数先判断输出栈 outStack 是否为空。

如果 outStack 不为空，那么直接从 outStack 的末尾弹出元素即可；
如果 outStack 为空，则需要将 inStack 中的所有元素倒入到 outStack 中，并且弹出 outStack 的末尾元素。

下面是一个简单的操作过程示例：

1️⃣. 初始状态，inStack 和 outStack 均为空

inStack: []
outStack: []

2️⃣. 调用 appendTail 函数，向队列尾部添加元素 1

inStack: [1]
outStack: []

3️⃣. 再次调用 appendTail 函数，向队列尾部添加元素 2

inStack: [1,2]
outStack: []

4️⃣. 调用 deleteHead 函数，从队列头部删除元素。此时 outStack 为空，需要将 inStack 中的所有元素倒入到 outStack 中

inStack: []
outStack: [2,1]

5️⃣. 调用 deleteHead 函数，从队列头部删除元素。此时 outStack 为空，需要将 inStack 中的所有元素倒入到 outStack 中

inStack: []
outStack: [2]

6️⃣. 再次调用 deleteHead 函数，从队列头部删除元素。此时 outStack 不为空，可以直接弹出 outStack 的末尾元素

inStack: []
outStack: []

7️⃣. 继续调用 deleteHead 函数，此时队列已经为空，返回 -1。
整个过程如下图所示：

   +---+        +---+
-->| 1 |        |   |
   +---+        +---+
-->| 2 |        | 2 |
   +---+        +---+
      inStack      outStack

(deleteHead)
   +---+        +---+
   |   |        | 1 |
   +---+        +---+
-->| 2 |        | 2 |
   +---+        +---+
      inStack      outStack

(deleteHead)
   +---+        +---+
   |   |        |   |
   +---+        +---+
   | 2 |        | 2 |
   +---+        +---+
      inStack      outStack

(deleteHead)
   +---+        +---+
   |   |        |   |
   +---+        +---+
   |   |        |   |
   +---+        +---+
      inStack      outStack

🌈代码

每行代码都有注释，详细明了🍎最贴心的代码了😢

var CQueue = function() {
    this.inStack = [];   // 定义一个输入栈
    this.outStack = [];  // 定义一个输出栈
};

CQueue.prototype.appendTail = function(value) {  // 实现队列尾部插入元素的方法
    this.inStack.push(value);  // 将元素插入输入栈
};

CQueue.prototype.deleteHead = function() {  // 实现队列头部删除元素的方法
    if (!this.outStack.length) {  // 如果输出栈为空
        if (!this.inStack.length) {  // 并且输入栈也为空
            return -1;  // 那么返回-1，表示无法删除元素
        }
        while (this.inStack.length) {  // 将输入栈中的所有元素都取出，放入输出栈中
            this.outStack.push(this.inStack.pop());
      }
    }
    return this.outStack.pop();  // 返回输出栈的栈顶元素，即为队列头部的元素
};

二、青蛙跳台阶问题

⭐️⭐️⭐️
原题

🔥 思路

这个问题可以用动态规划来解决。我们定义一个数组 dp，其中 dp[i] 表示跳到第 i 个台阶的跳法总数。对于第 i 个台阶，我们可以从第 i-1 和第 i-2 个台阶跳上来，因此有：
dp[i] = dp[i-1] + dp[i-2]
同时，当 i=0 时，按照题意应该返回 1，因此需要初始化 dp[0]=1。
当 i=1 时，只有一种跳法，因此 dp[1]=1。

最终答案为 dp[n]，由于题目要求对 1e9+7 取模，因此在计算 dp 数组的过程中也需要对每个值取模。

🌈代码

// 定义一个函数numWays，接收一个参数n
var numWays = function(n) {
    // 初始化a和b的值为1，用于计算F(0)和F(1)
    let a=1,b=1,sum;
    // 定义一个常量m等于1000000007，用于取模
    const m = 1000000007;
    // 使用for循环从0开始遍历到n-1，逐个计算F(0)到F(n-1)的值
    for(let i = 0; i < n; i++){
        // 计算当前项的值，即F(i+1)=F(i)+F(i-1)
        sum = (a + b) % m;
        // 将a更新为F(i)，b更新为F(i+1)，用于计算F(i+2)
        a = b;
        b = sum;
    }
    // 返回斐波那契数列第n项的值，即F(n)=F(n-1)+F(n-2)，这里返回F(n-1)
    return a;
};

三、矩阵中的路径

⭐️⭐️⭐️⭐️
原题

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。
如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。
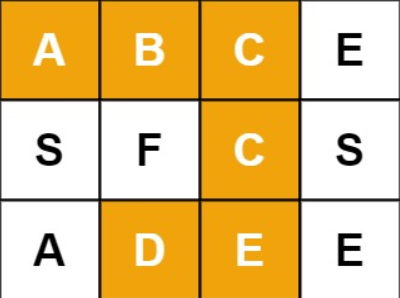
在这里插入图片描述

示例 1：
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true
示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

提示：
m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

🔥 思路

该题目要求在一个二维字符数组 board 中查找给定字符串 word 是否存在，
如果存在则返回 true，否则返回 false。

具体实现：首先将输入的字符串 word 转换成字符数组 words🐶，然后使用两个嵌套的循环遍历整个 board 数组，对于每个 (i, j) 点，尝试使用深度优先搜索（dfs）路径搜🍎来寻找是否满足要求。如果找到了匹配的字符串，则返回 true；如果没有找到，则返回 false。

dfs 函数用于检查当前点 (i,j) 是否可以作为字符串的下一个字符，并递归地向四个邻居进行搜索以查看是否可以继续匹配。如果当前点不符合条件或者已经访问过，则返回 false；否则尝试移动到下一步并继续搜索。为了避免重复访问同一个点，dfs 在访问每个点之前将其值设置为 \0，并且在返回之前将其恢复为原始值。

最后，如果整个 board 数组都被搜索过了，还没有找到符合要求的字符串，那么函数会返回 false。

🌈代码

class Solution {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();// 将word字符串转为字符数组
        for(int row=0 ;row<board.length;row++){// 遍历board数组的列
            for(int col=0;col<board[0].length;col++){// 遍历board数组的列
                if(def(board,words,row,col,0))return true;// 若找到匹配的字符串则返回true
            }
        }
        return false;// 若找到匹配的字符串则返回true
    } // 深度优先搜索，board为字符矩阵，word为要查找的字符串，i,j为当前遍历到的board中的字符位置，k为当前已经匹配的字符数
  
      boolean def(char[][] board,char[] words,int row,int col ,int index ){
        if(row<0||row>=board.length||col<0||col>=board[0].length||words[index]!=board[row][col])return false;// 如果i,j不在board矩阵的范围内，或board[i][j]字符不等于word[k]，则返回false
        if(index==words.length-1) return true;// 如果已经匹配完整个字符串，返回true
        board[row][col] ='.'; // 标记该字符已经被访问过
        boolean res = def(board,words,row+1,col,index+1)||def(board,words,row-1,col,index+1)||
        def(board,words,row,col+1,index+1)||def(board,words,row,col-1,index+1);// 递归搜索上下左右四个字符
        board[row][col]=words[index];// 将该字符的标记还原，以便后续搜索
        return res;// 返回搜索结果
    }
}

四、机器人的运动范围

⭐️⭐️⭐️⭐️
原题

🔥 思路

movingCount方法接受三个输入参数：整数m代表网格的行数，整数n代表网格的列数，以及整数k。该方法返回一个整数，表示从左上角出发，在条件限制下能够到达的格子数。
dfs方法是一个私有方法，用于进行深度优先搜索。它接受六个输入参数：整数×和y表示当前处理的单元格的横纵坐标，整数m和分别表示网格的行数和列数，整数k表示题目中的邹限制条件，布尔型二维数组ⅵsitd用于记录已经访问过的单元格。该方法返回一个整数，表示从当前单元格开始，在条件限制下能够到达的格子数。
sumXY方法接受一个整数sum,用于计算该整数的各位数字之和。该方法返回一个整数，表示各位数字之和。

在movingCount方法中，首先创建一个boolean类型的二维数组visited,用于记录每个单元格是否被访问过。然后调用dfs方法，并将起始坐标设置为(O,O)。最后，将dfs方法的返回值作movingCount方法的返回值。

在dfs方法中，首先判断当前单元格是否越界、是否已经被访问过或者其行和列索引之和是否大于k。

如果满足任条件，就返回0。
否则，将当前单元格标记为已访问，
然后递归调用右侧和下方的单元格，并将它们的结果累加返回。
在sumXY方法中，使用while循环对输入整数进行拆分求和，直到该整数变成0为止。

🌈代码

class Solution {
   
    // 计算各位数字之和
    private int sumXY(int sum){
        int res=0;
        while(sum!=0){
            res+=sum%10; // 取出最后一位数字，并加到结果中
            sum/=10;     // 将最后一位数字删除
        }
        return res;
    }
    
    // 深度优先搜索
    private int dfs(int x,int y,int m,int n,int k,boolean[][] visited){
        // 判断是否越界、是否已经访问过或者行列坐标之和是否大于 k
        if( x>=m|| y>=n||visited[x][y]||sumXY(x)+sumXY(y)>k) 
            return 0;
         
        visited[x][y]=true; // 标记当前单元格为已访问
        // 递归调用右侧和下方的单元格，并将它们的结果累加返回
        return 1+dfs(x+1,y,m,n,k,visited)+dfs(x,y+1,m,n,k,visited); 
    }
    
    // 计算在条件限制下能够到达的格子数
    public int movingCount(int m, int n, int k) { 
        boolean[][] visited= new boolean[m][n]; // 创建一个 boolean 类型的二维数组 visited，用于记录每个单元格是否被访问过
        // 调用 dfs 方法，并将起始坐标设置为 (0, 0)，最后将 dfs 方法的返回值作为 movingCount 方法的返回值
        return dfs(0,0,m,n,k,visited); 
    }
}

五、矩阵中的最长递增路径(难度: 困难)

⭐️⭐️⭐️⭐️⭐️
原题

🔥 思路

1️⃣. 定义dp数组：定义一个二维数组dp,其中dp表示以j)为起点的最长递增路径长度。
2️⃣. 状态转移方程：从每个位置开始向四个方向进行深度优先搜索(DFS)，求出能够到达的最长路径长度，并更新dp数组。状态转移方程为：dp]=max(dp[),1+
dp[y,其中(xy)为(j)的上下左右四个方向中比它大的位置。
3️⃣. 遍历dp数组：遍历dp数组，取最大值即可。
4️⃣. 使用记忆化搜索优化：由于可能会有重复计算，可以使用记忆化搜索的方法，在搜索过程中记录已经访问过的点的最长路径长度，避免重复计算。
5️⃣. 边界情况处理：需要注意边界情况的处理，例如避免访问不存在的位置等。
6️⃣.时间复杂度分析：时间复杂度为Omn),空间复杂度为0(mn),其中m和n分别是矩阵的行数和列数。

🌈代码

var longestIncreasingPath = function(matrix) {
    const m = matrix.length;
    const n = matrix[0].length;

    const dp = new Array(m).fill(0).map(() => new Array(n).fill(0)); // 初始化dp数组
    let res = 1;

    // 从每个位置开始dfs搜索，求出从该位置能到达的最长路径长度，并更新dp数组
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            res = Math.max(res, dfs(matrix, dp, i, j));
        }
    }
    return res;
};

function dfs(matrix, dp, i, j) {
    if (dp[i][j] !== 0) { // 如果已经计算过当前点的最长递增路径长度，则直接返回该值
        return dp[i][j];
    }

    const val = matrix[i][j];
    let maxLen = 1; // 初始化为1，因为每个点本身就构成了长度为1的递增路径
    const dirs = [[-1, 0], [1, 0], [0, -1], [0, 1]]; // 定义四个方向

    // 搜索从当前点出发能够到达的所有比当前点大的位置，并更新最长路径长度maxLen
    for (const dir of dirs) {
        const x = i + dir[0], y = j + dir[1];
        if (x >= 0 && x < matrix.length && y >= 0 && y < matrix[0].length && matrix[x][y] > val) {
            maxLen = Math.max(maxLen, 1 + dfs(matrix, dp, x, y));
        }
    }

    dp[i][j] = maxLen; // 将计算出的最长递增路径长度保存至dp数组
    return maxLen;
}

1 + dfs(matrix, dp, x, y) 表示从当前位置 (x, y) 出发，能够走过的最长路径长度。其中 1 表示当前位置本身就可以算作一步，而 dfs(matrix, dp, x, y) 则是递归地求解当前位置能够往四个方向延伸的最长路径长度，并返回该值。

这里使用了深度优先搜索（DFS）算法来遍历矩阵中的所有可能路径，根据题目要求，只能沿着非降序列前进，因此 DFS 时需要判断下一步是否符合条件，并仅在满足条件的情况下继续搜索。同时为了避免重复计算，可以使用一个二维数组 dp 来记录已经搜索过的位置的最长路径长度，避免重复计算。

总之，1 + dfs(matrix, dp, x, y) 的含义是当前位置 (x, y) 可以到达的最长路径长度，其中 1 表示当前位置本身就可以算作一步，dfs(matrix, dp, x, y) 则是递归地求解当前位置能够往四个方向延伸的最长路径长度。

六、剪绳子Ⅰ（贪心）

⭐️⭐️⭐️⭐️
原题

🔥 思路

当 j 为分割位置时，绳子被切成两段，一段长度为 j，另一段长度为 i-j。假设 dp[i-j] 存储的是长度为 i-j 的绳子的最大乘积，那么 jdp[i-j] 就是在这种情况下的最大乘积。

而另外一种情况是不再进行分割，此时长度为 i 的绳子的乘积就是 j(i-j)。因此，第6行计算的是在以 j 为分割位置时，能够获得的最大乘积，即 jdp[i-j] 和 j(i-j) 的较大值，其中 dp[i-j] 表示长度为 i-j 的绳子所能获得的最大乘积。

例如，当 i=8、j=3 时，绳子被切成两段，长度为 3 和 5。假设 dp[5]=6，则此时的最大乘积为 36=18 或者 35=15，两者取最大值 18，即 curMax=18。

🌈代码

class Solution {
    public int cuttingRope(int n) {
        int[] dp = new int[n + 1]; // 定义 dp 数组，dp[i] 存储长度为 i 的绳子的最大乘积
        for (int i = 2; i <= n; i++) { // 从长度为 2 开始计算最大乘积
            int curMax = 0; // 定义当前长度下的最大乘积
            for (int j = 1; j < i; j++) { // 枚举所有可能的分割位置
                curMax = Math.max(curMax, Math.max(j * (i - j), j * dp[i - j])); // 计算当前分割位置下的最大乘积，并更新 curMax
            }
            dp[i] = curMax; // 将当前长度下的最大乘积存储到 dp 数组中
        }
        return dp[n]; // 返回长度为 n 的绳子的最大乘积
    }
}